Изучим влияние турбулентной вязкости и диффузии плотности на параметры нарастающих во времени (неустойчивых) внутренних волн, распространяющихся в течениях с вертикальным сдвигом скорости. Аналогичные исследования в рамках модели идеальной жидкости проведены в работе [1]. Методы исследования устойчивости волновых возмущений в непрерывно стратифицированных турбулентных потоках изложены в [2,3].
Рассмотрим безграничный в горизонтальных направлениях слой непрерывно стратифицированной несжимаемой вязкой жидкости постоянной глубины H. Выберем начало прямоугольной системы координат xyz на дне, ось z направим вертикально вверх. Исследуем устойчивость волнового процесса с вектором скорости
происходящего на фоне
стационарного плоскопараллельного
течения, имеющего вертикальный сдвиг скорости
Запишем линеаризованные уравнения гидродинамики и граничные условия в виде [2,3]:
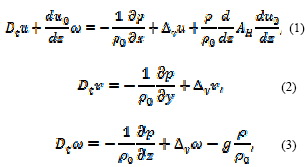
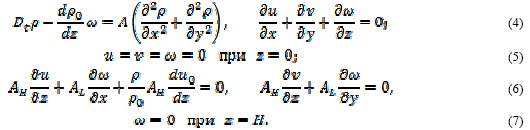
Здесь
и 
- коэффициенты
горизонтальной и вертикальной турбулентной вязкости 
- коэффициент горизонтальной диффузии плотности (А>0);
g - ускорение
свободного падения; ρ0(z) - стационарная плотность; ρ и ρ - динамические добавки давления и плотности.
Предполагается, что возмущение полей скорости, давления и плотности вызывается только внутренними волнами. Это позволяет в краевой задаче для волновых флуктуаций заменить кинематическое и динамическое граничные условия одним граничным условием, которое «отфильтровывает» поверхностные волны [4,5].
Введем безразмерные переменные и функции
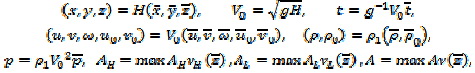
где ρ1 - некоторое среднее постоянное значение плотности. Неизвестные функции u, v, ω, р, ρ будем разыскивать в форме
Переходя в (1)-(8) к
безразмерным переменным и подставляя (9), получим после несложных
преобразований однородную задачу относительно 
(штрихами обозначены производные по 
):
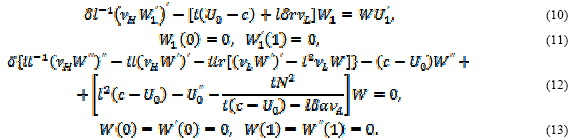
Здесь
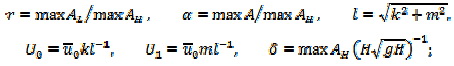
к, m - безразмерные волновые числа 
- безразмерная фазовая скорость 
безразмерная частота
Вяйсяля-Брента; 
- глобальное число Рейнольдса.
Глобальное число Ричардсона в данном случае выбрано равным единице 
. При 
(ν - кинематический коэффициент
вязкости) уравнение (12) совпадает с уравнением Орра-Зоммерфельда [6].
Предполагая функции 
и значения величин m, к, δ, r, α заданными, выберем в качестве
параметра однородной краевой задачи (10)-( 13) безразмерную фазовую скорость с.
Докажем,
что все собственные значения однородной задачи (10), (11) 
лежат в полу полосе
где с = са + ic1 Умножим уравнение (10) на комплексно сопряженную с W1 функцию W1* и проинтегрируем по z от 0 до 1. Тогда, учитывая (11), имеем
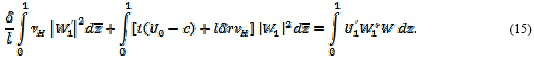
Полагая в (15) U1´ = 0 и выделяя затем действительную и мнимую части, находим (черту при z далее опускаем)
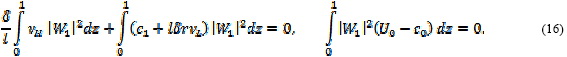
Используя неравенство Коши-Буняковского и учитывая граничные условия (11), (13) в точке z = 0, получаем:
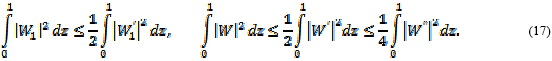
Из (16) и первого неравенства (17) следует, что собственных значений однородной задачи (10), (11) вне области (14) не существует.
Рассмотрим теперь краевую задачу (12), (13). Представим уравнение (13) в виде:
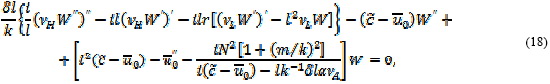
где 
Если обозначить к
то уравнение (18) и граничные
условия (13) совпадают с краевой задачей, которая описывает двумерные возмущения (т.е.
возмущения, у которых m = 0, V = 0). Таким образом, в силу
оценки (14) будет справедливо утверждение
о том, что трехмерная задача (10)-( 13) имеет дополнительный спектр собственных значений c, не
содержащийся в двумерной задаче, но он соответствует устойчивым возмущениям, с] < 0 (аналог теоремы Романова [7]).
На основании данного утверждения можно сделать вывод, что все собственные
значения задачи (10)-(13), соответствующие неустойчивым возмущениям, содержатся в спектре однородной
краевой задачи (12), (13). Следовательно, если существует неустойчивое трехмерное
возмущение с фазовой скоростью с, то существует и неустойчивое двумерное возмущение с такой же фазовой
скоростью, но (см.(19)) уже при меньшем значении числа Рейнольдса и большем значении числа
Ричардсона (аналог теоремы Сквайра). Это
позволяет при изучении неустойчивых волновых
возмущений свести исследование исходной краевой задачи (10)-(13) к анализу более простой спектральной задачи (12)-(13). Умножим
уравнение (12) на комплексно сопряженную с W функцию W и проинтегрируем по z от 0 до
1. Тогда, учитывая (13), запишем мнимую часть полученного равенства в виде:
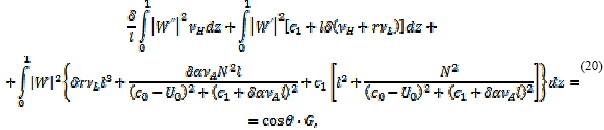
где 9 -
угол набегания волны на поток 
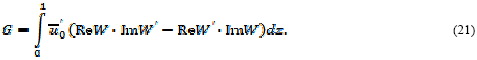
Равенство (20) выполняется тождественно, когда с = c0 + tc1 является собственным значением однородной краевой задачи (12), (13). Используя обобщенную теорему о среднем и соотношения (17), получаем, что в случае неустойчивых волновых возмущений (c1 > 0) равенство (20) нарушается при
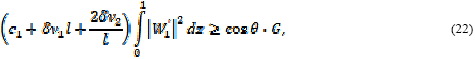
где 
Принимая во внимание очевидные соотношения (см. (21), (17)):
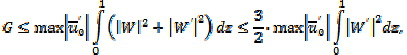
находим из (22) неравенство
которое обеспечивает реализацию условия (22). Следовательно, для существования неустойчивых волновых возмущений (с1 > О) необходима перемена знака в неравенстве (23). Умножая обе части неравенства (23) на l и меняя его знак на противоположный, получаем для величины экспоненциального показателя роста амплитуд волновых возмущений (инкремента внутренних волн) такую оценку:
СПИСОК ЛИТЕРАТУРЫ:
1. Маков Ю.Н., Степанянц Ю.А. О влиянии кривизны профиля скорости на параметры нарастающих волн в сдвиговых потоках // Океанология. - 1984. -24, вып. 4. - С. 578-585.
2. Хартиев С.М., Черкесов Л.В. Влияние вязкости жидкости и силы Кориолиса на устойчивость внутренних волн // Докл. АН УССР. Сер. А. - 1983. -№3. - С. 61-65.
3. Букатов А.Е., Власенко В.И., Пухтяр Л.Д. и др. Динамика поверхностных и внутренних волн. -Киев: Наук. думка, 1988. - 192 с.
4. Черкесов Л. В., Иванов В. А., Хартиев С. М. Введение в гидродинамику и теорию волн. - Санкт-Петербург: Гидрометеоиздат, 1992. - 264 с.
5. Потетюнко Э.Н., Черкесов Л.В., Шубин Д.С., Щербак Е.Н. Свободные колебания и обратные спектральные задачи. Волновые движения неоднородной жидкости. - М.: Вузов. книга, 2001. - 288 с.
6. Бетчов Р., Криминале В. Вопросы гидродинамической устойчивости. - М.: Мир, 1971. - 350 с.
7. Дикий Л. А. Гидродинамическая устойчивость и динамика атмосферы. - Л.: Гидрометеоиздат, 1976. - 108 с.