Многофазные среды часто встречаются в природе и в различных областях человеческой деятельности. В с вязи с этим, актуальным является исследование механизма воздействия динамических нагрузок на многофазные массивы, кинетика и динамика волновых процессов, возникающих в них, как реакция на эти воздействия.
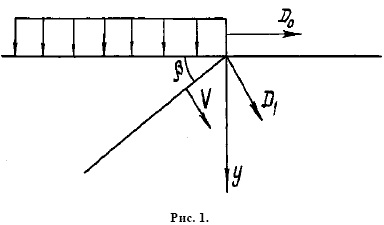
1. Рассмотрим среду, состоящую из трех фаз, которая занимает нижнее полупространство. Возьмем начало координат на свободной поверхности, ось у направим внутрь среды, а ось х по границе среды вправо. Пусть на границе среды приложена постоянная по величине нагрузка, передний фронт которой бежит с постоянной скоростью D0 вдоль границы.
Исследуем волновое движение трехфазной среды, возбужденное таким источником.
Решение этой задачи проводится на основе взаимопроникающих движений сжимающей жидкости [1] и односкоростной теории трехфазной среды [2]. Следуя [3, 4], введем обозначения.
Приведенную плотность i - ой фазы (i = 1, 2, 3) обозначим ρi, а ее истинную плотность через ρi° тогда плотность трехфазной среды выразится
ρ=ρ1+ρ2+ρ3
Объемные доли фаз среды
определяются
![]()
Для каждой фазы среды примем закон независимой сжимаемости фаз и давление всех фаз считаем совпадающими и равными давлению Р среды.
Припишем индекс "0" параметрам смеси в некотором начальном состоянии, тогда
При распространении ударной волны в трехфазной среде примем для газовой фазы среды адиабату Гюгонио, а для жидкой и твердой фаз используем уравнение сжатия
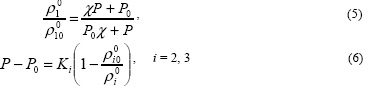
где γ - показатель адиабаты воздуха, Ki - модуль объемного сжатия соотвествующей фазы.
Пусть v - скорость частиц среды на ударной волне, движущейся со скоростью D1 трехфазной среде (перед волной среда покоится). На ударной волне имеем
Кроме уравнения сохранения массы и количества движения запишем уравнение энергии для трехфазной среды
E1, E2, E3- приращение внутренних энергий единицы массы соответствующих фаз, которые имеют вид
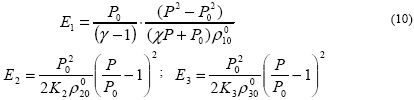
Из соотношений (5) - (10) получим уравнение состояния трехфазной среды,
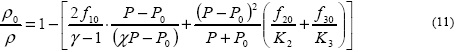
а затем определим скорость фронта ударной волны в среде и скорость частиц среды на ней в начальной точке 0.

Скорость звука в трехфазной среде выразится:
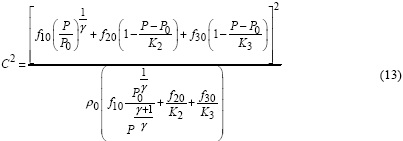
Задавая величину бегущей нагрузки получим ее скорость на границе и угол наклона фронта в точке локализации внешнего воздействия
Зная угол наклона ударной волны к границе, можно определить составляющие скорости частиц по осям координат
![]()
2. Рассмотрим задачу о двумерном движении трехфазной среды (типа смеси воздух-вода-кварц), которая инициируется бегущей вдоль плоской границы волновой нагрузкой переменного профиля. Вид профиля нагрузки неизвестен. Область возмущенного движения среды ограничена ударной волной, форму которой задаем уравнением.
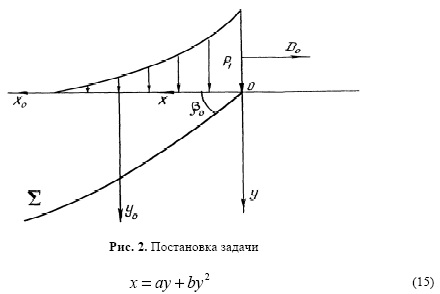
где а, b- коэффициенты, зависящие от содержания фаз в среде и давления среды. Действительно
![]()
при x = y = 0 значении в = во начальному углу наклона a = ctg β0.
Предположим, что изменение угла наклона касательной к ударной волне в среде на a при y = y дается выражением
![]()
Такое определение гарантирует нам реальные значения коэффициентов. Обращаем внимание, что определение угла в было дано в первой части. Угол изменяется от начального значения в зависимости от числа "шагов" вдоль ударной волны в среде.
![]()
где n - число шагов, а - величина шага по углу. Число шагов определяется из условия, что скорость фронта ударной волны в среде должна быть больше, чем местная скорость звука со стороны невозмущенной области.
![]()
Давление со стороны невозмущенной области определяется по формуле:
![]()
где y - глубина полупространства среды, g - ускорение свободного падения
![]()
y∑ - глубина полупространства среды по ударной волне.
Изменение плотности среды ρy с глубиной учитывается, исходя из уравнения состояния трехфазной среды.
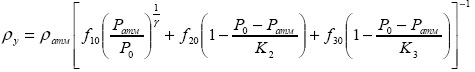
ρ - плотность среды при атмосферном давлении.
По изложенной в первой части методике определяем все параметры на ударной волне (сделав n -шагов).
После формирования параметров на ударной волне, приступаем к решению искомой задачи - определению закона изменения бегущей нагрузки на границе среды и параметров возмущенного движения среды, вызванное этой нагрузкой переменного профиля, значение которой известно только в начальной точке 0. Решается обратная задача. В неподвижной координатной системе (x0,y0) движение будет неустановившимся. Введем координатную систему (x,y) связанную с движущимся фронтом нагрузки, тогда движение среды в этой системе будет установившимся. Уравнения движения и неразрывности в подвижной системе координат принимают вид:
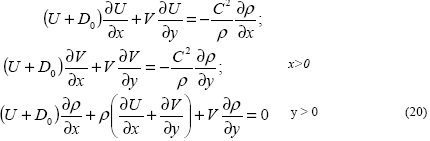
Рассматривается случай вихревого движения, поэтому вводим функцию тока и вихрь
Для трехфазной среды имеем уравнение состояния среды, полученное в первой части
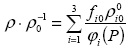
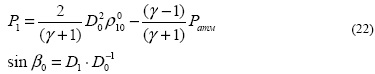
Расчет в области возмущения проводится методом характеристик. Условия на характеристиках запишутся так:
![]()
где A, B - коэффициенты, которые определяются ниже.
Пусть λ - характеристическое направление, определяемое зависимостью
Тогда
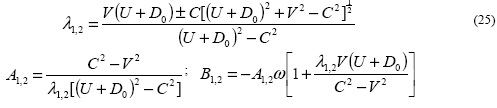
Верхний знак (+) в (25) соответствует характеристикам первого семейства, а нижний (-) - второго семейства.
Очевидно, для случая (U + D0)2 + V2 < C2 характеристические направления отсутствуют.
Зная в точке 0 угол β0 , давление р и скорость фронта ударной волны D1 в трехфазной среде определим все параметры на ударной волне. Принимая эти параметры за начальные ("нулевой" слой), формируем первый слой.
Рассмотрим две точки, лежащие на ударной волне. Обозначим их индексами (n - 1, m) и (n - 1, m +1); n - номер слоя, а m - номер точки на этом слое
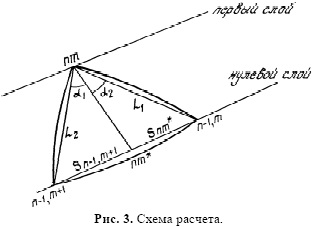
Из точки (n - 1, m) проводим характеристику первого семейства, из (n - 1, m +1) - второго семейства. Точку (n, m) определим как пересечение характеристик плоскости x,y. Приняв во внимание, что линия тока делит угол между характеристиками пополам, определяем параметры точки (n, m ). Шаг на ударной волне задаем так, чтобы взятые точки находились достаточно близко и элемент кривой между ними можно было принять за прямую. Для определения U и V в узловой точке (n, m) имеем
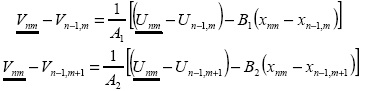
Искомые значения подчеркнуты дважды, значения A1 2, B1 2 определяются в точках (n - 1, m) и (n - 1, m + 1) нижнего слоя. Координаты узла (n, m) определяются из соотношений
Вихрь выразим
![]()
Параметры в точке (n, m*) определим, исходя из соотношений
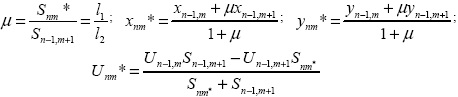
Аналогично находим параметры Vnm* Pnm* Рnm* Cnm*. Далее получим связь между скоростями U, V и давлением в узле (n, m).
Вдоль линии тока применительно к движению трехфазной среды получим
уравнение
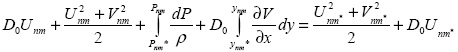
где
интеграл
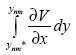 представим
через конечные разности
представим
через конечные разности
Исходя из уравнения состояния для трехфазной среды получим
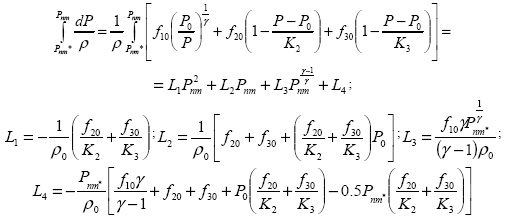
Окончательно связь параметров в узлах (n, m) и (n, m*) принимает вид:
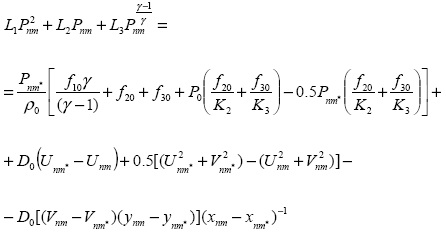
Откуда вычисляется Pnm , а затем из уравнения состояния вычисляется плотность трехфазной среды в узле (n,m).
Из формулы полученной для скорости звука в трехфазной среде (в части первой) вычисляется скорость звука в точке (n,m).
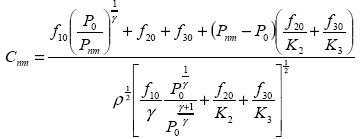
Таким образом просчитываем все точки первого "слоя", затем второго "слоя" и т. д. и выходим на границу y=0.
На основе вышеприведенной модели задача решена численно на ЭВМ. Показано, что размер возмущенной области при больших скоростях распространения значительно превышает длину бегущей нагрузки.
СПИСОК ЛИТЕРАТУРЫ:
1. Рахматулин Х. А. Основы газодинамики взаимопроникающих движений сжимаемых сред. ПММ, т.20, №2, 1956.
2. Ляхов Г. М. Ударные волны в многокомпонентных средах. Изв. АН СССР, ОТН, Механика и машиностроение, №1, 1959.
3. Рахматулин Х. А. О распространении волн в многокомпонентных средах. ПММ, т.33, 1969.
4. Рахматулин Х.А., Кубанова А.К. Проникание вглубь полупространства из трехкомпонентной среды бегущей по его границе постоянного давления. В кн. "Гидродинамика одно- и двухфазных сред". Из-во ФАН, Ташкент 1982.

