В работе дано обоснование метода фиктивных областей для одного класса нелинейных краевых задач. Впервые получена неулучшаемая оценка скорости сходимости решения вспомогательной задачи к решению исходной задачи, при стремлении к нулю малого параметра.
Метод фиктивных областей
является одним из известных методов приближенного решения краевых задач
математической физики.
В основном метод фиктивных областей обоснован для линейных краевых задач
математической физики.
Данная работа посвящена обоснованию метода фиктивных областей для нелинейных эллиптических уравнений. Предлагается новый способ получения неулучшаемой оценки скорости сходимости решения в методе фиктивных областей.
Рассмотрим краевую задачу для
нелинейных эллиптических уравнений в области 
с
границей S
(1)
(2)
Согласно методу фиктивных
областей продолжением по младшему коэффициенту в вспомогательной области 
с
границей 
, решается уравнение с малым параметром
(3)
, (4)
где f -
продолжен нулем вне 
и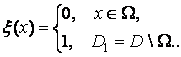 
Дальнейшие используемые обозначения взяты из монографии.
Определение 2.1.1. Обобщенным
решением задачи (3), (4) называется функция 
, удовлетворяющая интегральному тождеству
(5)
для
всех 
.
Теорема 1. Пусть
. Тогда существует единственное обобщенное решение
задачи (3)-(4) и для него справедлива оценка
(6)
где
,
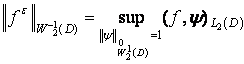причем, при ε→0 данное решение сходится к обобщенному решению задачи (1), (2).
Определение 2. Сильным
решением задачи (3)-(4) называется функция 
, удовлетворяющая уравнению (3) почти всюду.
Теорема 2.1.2. Пусть 
Тогда существует сильное решение задачи (3)-(4) и
для него имеет место оценка
где C→∞, при ε→0. (7)
Теорема 3. Пусть . Тогда 
(8)
С0-положительная постоянная, не зависящая от ε.