Постановка проблемы. Развитие компетентностного подхода в обучении студентов педагогических вузов, в том числе будущих педагогов – учителей музыки (далее – УМ) является актуальной задачей высшего образования. Анализ проведенных исследований в этой области (авторы М.М. Брянцев, Г.В. Карягина, А.И. Марков, О.А. Подкопаева, О.Ю. Праздничных, А.С. Приселков, О.Н. Чигинцева, Н.Ф. Талызин, А.В. Хуторской и др.) показал значительно возросший интерес к изучению применения музыкально-компьютерных технологий (далее – МКТ) в направлении педагогического процесса формирования и обретения УМ профессиональных знаний. При этом, основные разработки МКТ выполнены по части развития композиторского мышления и творчества и лишь косвенно соприкасаются с педагогикой обучения УМ в вузе. На математическом уровне недостаточно изучены теоретические основы методологии процесса формирования компетентности будущими УМ. Существующие математические модели педагогических технологий (авторы Б. Битинас, В.М. Блинова, В.И. Загвязинский, В.И. Михеев, В.Я. Якунин и др.), в основном, связаны с применением теорий множеств, игр, вариационных, графовых, вероятностных статистических математических методов, ограничивающих описание обучения учащихся только в группах, а не отдельного взятого индивидуума, что ограничивает применение их в педагогической практике.
Цель работы – с помощью математического метода анализа описать функцию формирования профессиональной компетентности УМ средствами МКТ.
Изложение и обоснование полученных автором результатов. Компетентностный подход в образовании предусматривает формирование профессиональной компетентности путем освоения учащимся отдельных компетенций от ключевых общеобразовательных до предметных, соответствующих профильному образованию. Очевидно, что для будущего УМ функции проявления предметных компетенций: уровня технического мастерства игры на музыкальном инструменте – Х; уровня художественного мастерства игры на инструменте – ξ; уровня освоения предметных профильных компетенций МКТ по приоритетным направлениям применения компьютерных средств в обучении – Y (в предыдущих работах автора были раскрыты профильные компетенции на базе применения современных МКТ по отношению к ключевой эманационно-педагогической компетенции УМ), являются основными переменными функциональными факторами (функциями влияния), функции F – профессиональной компетентности будущего УМ:
F = f (X, ξ, Y). (1)
Математическая модель в общем виде представлена автором дифференциальным уравнением первого порядка с разделяющими переменными в форме полного дифференциала в частных производных
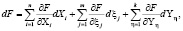(2)
где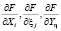 
– частные производные соответствующих переменных Х (Х1, ..., Хn); ξ (ξ1, ..., ξm), Y(Y1, ..., Yk), а каждая частная производная характеризует вклад функций влияния каждого из факторов в F функцию; n, m, k – число учитываемых факторов соответственно по функциям Х, ξ, Y; а dXi, dξj, dYη – независимые конечные приращения функций влияния и их количество равно количеству влияющих факторов (от предметных компетенций). Причем, каждый из них задан в явном виде, что позволяет нам описывать функции влияния каждого фактора в отдельности. В процессе обучения УМ формирование компетенций происходит во времени τ, что соответствует изменению функций влияния во времени с независимым временным конечным аргументом – dτ. После подстановки функций в (2), получаем описание математической модели в таком виде
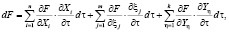(3)
где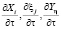 
– скорости освоения соответствующих предметных компетенций УМ. Задав границы рассмотрения влияющих факторов рамками приоритетных направлений применимости технических средств МКТ, получаем следующие основные функции влияния: Х1, – освоение УМ чистоты интонации звучания при игре на музыкальном инструменте; Х2 – освоение УМ заданного ритмического рисунка и агогических особенностей игры; Х3 – влияние на технику исполнения музыкального произведения других неучтенных факторов; ξ1 – освоение УМ элементов и приемов художественного исполнения музыкальных произведений: вибрато, реверберация, тремоли, изменения угла атаки и затухания звука, компрессора и экпандера звуковой панорамы и др.; ξ2 – влияние на художественную окраску музыкального произведения других неучтенных факторов; Y1 – овладение театральным артистизмом подачи музыкального материала ученикам; Y2 – освоение УМ элементами сольного вокального пения и импровизации, синтеза и «рисования» музыки с помощью компьютера; Y3 – овладение УМ театральным мастерством сценариста, режиссера и постановщика уроков музыки; Y4 – овладение УМ навыками звукового режиссера по обеспечению качества многомерного звучания в неприспособленных для этого помещениях; Y5 – освоение УМ эффективных приемов трансляции ученикам музыкального искусства по аудио, видео, кинестатичному, дискретному каналам восприятия информации; Y6 –овладение УМ коммуникативными навыками музыкального общения с учениками (эмпатийной, фасилитаторской и аттрактивной функциями); Y7 – влияние других неучтенных компетенций.
С учетом описанных выше функций влияния (подстановки n = 3, m = 3, η = 7), и рассматривая процесс формирования профессиональной компетентности УМ в динамике овладения указанными предметными компетенциями во времени τ, описание математической модели педагогического процесса формирования профессиональной компетентности УМ окончательно принимает такой вид:
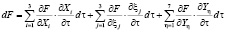. (4)
Адекватность этой математической модели была подтверждена с помощью критерия Фишера (Ϯ-критерия, при уровне значимости ρ = 0,05) в ходе проведения констатирующего и формирующего экспериментов, организованных в Харьковской гуманитарно-педагогической академии Харьковского областного совета на факультете иностранной филологии и музыкального искусства в 2012–2013 гг.
Выводы. Предложенная автором математическая модель адекватно описывает педагогический технологический процесс профессионального обучения в части формирования профессиональной компетентности будущего УМ на основе освоения им предметных компетенций средствами музыкально-компьютерных технологий и в принципе может выполнять описательную, управленческую, исследовательскую, интерпретационную и прогностическую функции для педагогики обучения будущих УМ. Общее и частные решения предложенного автором дифференциального уравнения могут быть с успехом применены при проведении исследований и в других областях педагогики.