Постановка проблемы. Одной из важных задач компетентностного обучения является формирование готовности у будущих музыкальных руководителей (далее – МР) детских дошкольных учреждений применять инновационные технологии (далее – ИТ).
Анализ проведенных исследований в этой области показал наличие значительного количества публикаций по разработкам новых педагогических технологий: для вузов (И.С. Батракова, В.И. Боголюбов, В.В. Давыдов, Е.И. Казакова, М.В. Кларин, Н.Н. Михайлова, Г.К. Селевко и др.); по формированию готовности применять ИТ (И.Ю. Горохова, И.А. Зимняя, Л.А. Кандыбович, В.А. Крутецкий, В.А. Сластенин, Т.В. Петрученко, Л.С. Подымова и др.); по формированию компетентности будущих педагогов (В.В. Гузеев, Ж.Д. Кармазина, А.К. Маркова, Л.М. Митина, Н.Ф. Талызин, А.В. Хуторской и др.). Между тем, учеными недостаточно исследован в теоретическом плане педагогический процесс формирования готовности будущих МР для применения ИТ, не рассмотрены возможности его абстрактно-математического моделирования для решения актуальных проблем педагогики. Данная проблема ранее не была предметом специального научно-педагогического исследования. Существующие в педагогике математические модели (авторы: Дж. Гласс, Б. Ительсон, В.И. Загвязинский, К.Я. Краснянская, Г.В. Суходольский, В.С. Черепанов и др.) не предназначены для описания данного педагогического процесса.
Цель работы – абстрактно-математической моделью описать процесс формирования готовности будущих МР применять ИТ в контексте компетентностного подхода.
Изложение и обоснование полученных автором результатов. Компетентностный подход обучения будущих МР в вузах направлен на формирование профессиональной компетентности, в составе которой мы предусматриваем освоение специальных компетенций готовности (далее – КГ) МР по применению ИТ в детских дошкольных учреждениях. Предлагаемая нами абстрактно-математическая модель основана на результатах наших ранних публикаций, где была предложена математическая модель процесса обучения игре на музыкальном инструменте и обоснованы для МР теоретические аспекты освоения КГ.
Авторская абстрактно-математическая модель учитывает следующие основные функции влияния КГ на процесс F. По когнитивным КГ: Х1 – владение чистотой интонации звучания инструмента; Х2 – овладение темпо-ритмом и агогическими приемами исполнения для восприятия детской аудиторией форм и стилей музыкальных произведений; Х3 – умение исполнять специальные технические приемы игры: гаммы, арпеджио, трезвучия для обучения детей закономерностям построения лада музыки; Х4 – владение небходимой скоростью исполнения музыкальных произведений; Х5 – владение на уровне музыканта-профессионала музыкальными инструментами (основным и компьтерным) для подачи ИТ детям; ξ1 – умение выдерживать заданный динамический план музыкального произведения, его фразировку при подаче детям новых форм произведений; ξ2 – обладать умениями концертмейстера (обеспечить сыгранность пения детей и музыкального аккомпанимента); ξ3 – владение компьтерными приемами украшения звучания музыки (эхо, хорус, частотная и амплитудная одноголосная и многоголосная реверберация) для выработки у детей эмоционального фона восприятия музыки; ξ4 – владение искусством выполнения художественного приема «вибрация» для передачи музыкального настроения детской аудитории; Y1 – владение современными ИТ, в том числе компьютерными МИДИ технологиями для занятий с детьми; Y2 – владение музыкальными редакторами звуковысотной коррекции голоса для работы с интонационно – «трудными» детьми, а также для случая временной потери голоса у МР; Y3 – владение музыкальным редактором редукции многоголосных партий музыкальных произведений для возможности сыграть детям «в живую» отрывки из опер, оперет, мьюзиклов и др.; Y4 – владение редакторами перевода звуков в рисунок и рисование звуком для развития музыкально-художественного творчества у детей; Y5 – владение компьютерными редакторами «караоке», «минусовок» для развития пения у детей. По операционно-деятельностным КГ: U1 – умение петь с листа, транспонировать произведения в другую тональность, что необходимо для создания творческих дуэтов, хора и детских ансамблей; U2 – умение дирижирования пением детей, в том числе многоголосным детским хором; U3 – овладение приемами театрального мастерства по освобождению мышц, общения (жесты, мимика, речь), представления; творческого внимания, воображения и вдохновения подачи музыки детскому слушателю; U4 – овладение аттрактивной функцией к аудитории юных слушателей, способностью доставлять духовное наслаждение; U5 – овладение фасилитаторской функцией общения с детьми; U6 – овладение синтонной функцией – подстройки под детскую аудиторию; U7 – умение режиссера для постановки занятий с детьми в игровой, театральной форме; U8 – умения хореографа-постановщика танцев детей. По акмеологическим КГ: Z1 – умение трансляции музыкальных знаний детям по аудио, видео, кинестатичному информационных каналах восприятия; Z4 – личностное умение донести до юного слушателя все краски эмоциональной палитры и колорита звучания музыки; Z5 – неучтенные КГ в части готовности применения ИП.
Абстрактно-математическая модель процесса формирования готовности МР к применению ИТ (объект F) во времени τ представлена нами в виде дифференциального уравнения первого порядка в форме полного дифференциала в частных прозводных с разделяющими переменными
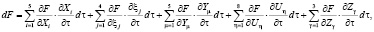(1)
где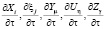 
– частные производные функций КГ, которые характеризуют скорость освоения МР соответствующих КГ на отрезке времени dτ; 
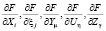– частные производные по соответствующим переменным Х, ξ, Y, U, Z. Учитывая, что функции Х, ξ, Y, U, Z существуют и являются монотонно изменяющими, их всегда можно аппроксимировать линейно – кусочными зависимостями при условии достаточно малых приращений аргумента – dτ. С учетом этого, (1) принимает окончательный вид:
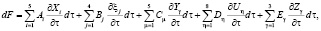(2)
где Аi , Bj , Cμ , Dη , Eγ – коэффициенты, учитывающие долю вклада соответствующих переменных Xi , ξj ,Yμ , Uη ,Zγ в изменение функции dF на отрезке времени dτ.
Адекватность абстрактно – математической модели была проверена с помощью критерия Фишера (Ϯ-критерия, при уровне значимости ρ = 0,05) и подтверждена в ходе проведения констатирующего и формирующего экспериментов, организованных в Харьковской гуманитарно-педагогической академии Харьковского областного совета на факультете иностранной филологии и музыкального искусства в 2013 г.
Выводы. Автором теоретически разработана и экспериментально подтверждена абстрактно-математическая модель процесса формирования готовности у будущих МР применять ИТ, которая позволяет выполнять анализирующую, синтезирующую, исследовательскую и прогностическую педагогические функции на любом этапе компетентностного обучения будущих МР и может быть полезна другим преподавателям музыкального искусства в части теоретического описания процесса готовности педагогов к той или иной инновационной педагогической деятельности.