В работе для линейных гиперболических уравнений в области с отходом от характеристики доказаны корректности задач Дирихле и Пуанкаре.
В теории уравнений частных производных гиперболического типа краевые задачи с данными на всей границе области служат примером некорректно поставленных задач [1]. В данной работе для линейных гиперболических уравнений в области с отходом от характеристики доказаны корректности задач Дирихле и Пуанкаре.
п.1. Постановка задач и результаты. Пусть D ⊂ R2 – конечная область, ограниченная отрезком АВ: 0 ≤ x ≤ 1 оси y = 0, а при y > 0 – гладкой кривой АС: y = γ(x) < x, вдоль которой 0 < γ′(x) < 1 и прямой ВС: y = 1 – x.
В области D рассмотрим уравнение
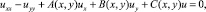 (1)
(1)
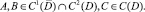
В качестве задачи Дирихле и Пуанкаре рассмотрим следующие задачи
Задача 1. Найти в области D решение уравнения (1) из класса 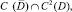 удовлетворяющее краевым условиям
удовлетворяющее краевым условиям
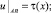
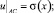
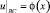 (2)
(2)
или
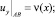
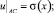
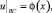 (3)
(3)
где
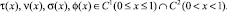
В характеристических координатах ξ = x + y, η = x – y уравнение (1) записывается следующим образом
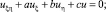 (4)
(4)
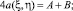
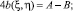
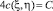
При этом краевые условия (2) и (3) соответственно имеют вид
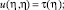
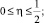
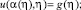
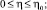 (5)
(5)
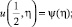
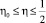
или
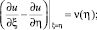
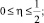
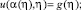
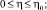 (6)
(6)
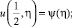
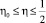 ,
,
где 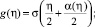
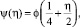 , а функция ξ = α(η) является решением уравнения
, а функция ξ = α(η) является решением уравнения 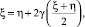 при этом
при этом 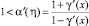 , 0 < η < 1, а также
, 0 < η < 1, а также 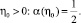
Пусть, в случае задачи (4), (5), выполняется условие
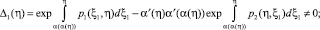 (7)
(7)
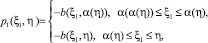
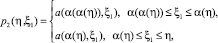
а в случае задачи (4), (6) имеет место
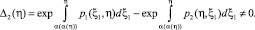 (8)
(8)
Тогда справедлива
Теорема 1. Задача 1 однозначно разрешима.
п. 2. Доказательство теоремы 1. Сначала рассмотрим задачу (4), (5). Используя общее решение уравнения (4) [2], нетрудно показать, что решение задачи Коши для уравнения (4) представимо в виде
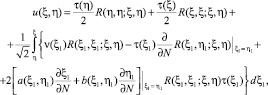 (9)
(9)
где R(ξ1, η1, ξ, η) – функция Римана уравнения (6), а
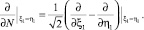
Из (8), при 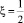 и ξ = α(η), используя краевое условие (5), получим интегральные уравнения первого рода
и ξ = α(η), используя краевое условие (5), получим интегральные уравнения первого рода
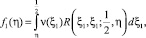
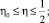
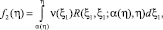 0 ≤ η ≤ η0,
0 ≤ η ≤ η0,
где
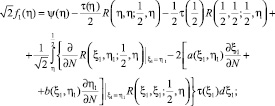
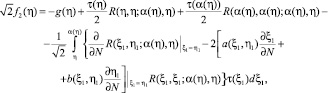
которые дифференцированием сводятся, соответственно, к следующему интегральному уравнению Вольтерра второго рода
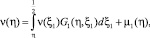 (10)
(10)
и функционально-интегральному уравнению
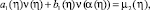 (11)
(11)
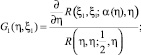
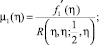
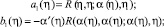
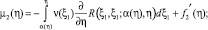
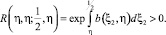
В [3] показано, что, если
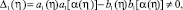 (12)
(12)
то функциональное уравнение (11) имеет единственное решение вида
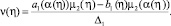 (13)
(13)
Из определения функции Римана R [2,4], формула (12) записывается в виде (7), а (13) – в следующем виде
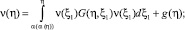 (14)
(14)
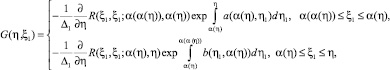
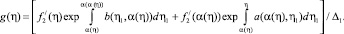
Известно, что функция Римана R по переменным ξ1, η1 и ξ, η имеет такую же гладкость, что и коэффициенты уравнения (4) [4], поэтому ядро G(ξ, ξ1) допускает оценку
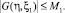 (15)
(15)
Решение интегрального уравнения (15) будем искать в виде ряда
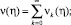 (16)
(16)
ν0(η) = g(η);
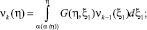 k = 1, 2, ... .
k = 1, 2, ... .
Из (15) получим следующие оценки
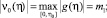
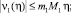
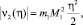
и вообще 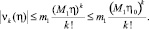 .
.
Тогда, для ряда (16) будем иметь
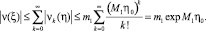
Таким образом, интегральное уравнение (14), (а также (11)), при выполнении условия (7), однозначно разрешимо.
Следовательно, задача (4), (5) имеет единственное решение вида (8), в котором ν(η) находятся из уравнений (10) и (14).
Теорема 1 для задачи (1), (2) доказана.
Теперь рассмотрим задачу (1), (3), которая переходит к задаче (4), (6). В этом случае, из (8), при 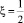 и ξ = α(η), с учетом (6), получим следующее интегральное уравнение Вольтерра второго рода
и ξ = α(η), с учетом (6), получим следующее интегральное уравнение Вольтерра второго рода
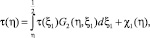
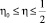 (17)
(17)
и функционально – интегральное уравнение
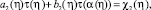
0 ≤ η ≤ η0, (18)
где
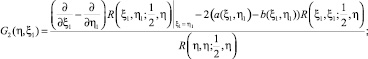
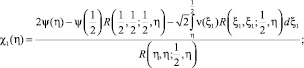
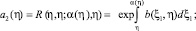
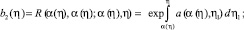
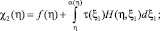
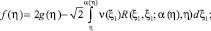
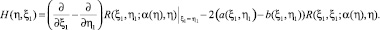
Если выполняется условие
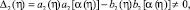
или, это тоже самое, условие (8), то функциональное уравнение (18) имеет единственное решение вида
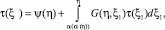
0 ≤ η ≤ η0, (19)
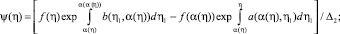
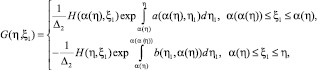
при этом
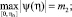
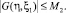
Решение интегрального уравнения (19) будем искать в виде ряда 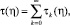 для которого имеет место неравенство
для которого имеет место неравенство 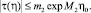
Таким образом, интегральное уравнение (19) (а также (18)), при выполнении условия (8), однозначно разрешимо.
Следовательно, задача (4), (6) имеет единственное решение вида (9), в котором τ(ξ) определяются из уравнений (17) и (19).
Отметим, что, если A(x, y) = B(x, y) ≡ 0, то условие (8) не выполняется. В этом случае уравнение (18) имеет вид
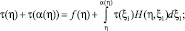 (20)
(20)
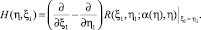
Так как интегральный оператор, стоящий в правой части равенства (20), вполне непрерывен, то, как показано в [3], функциональное уравнение (20) имеет единственное решение.
Таким образом, и в этом случае задача (4), (6) однозначно разрешима.
Теорема 1 для задачи (1), (3) доказана.
Отметим, что краевые задачи с отходом от характеристики для уравнения (1) изучены в [5].

