В работе для линейных гиперболических уравнений в области с отходом от характеристики доказаны корректности задач Дирихле и Пуанкаре.
В теории уравнений частных производных гиперболического типа краевые задачи с данными на всей границе области служат примером некорректно поставленных задач [1, 2]. В данной работе для линейных гиперболических уравнений, в области с отходом от характеристики, доказаны корректности задач Дирихле и Пуанкаре.
п. 1. Постановка задач и результаты. Рассмотрим линейное гиперболическое уравнение
uxx – uyy + A(x, y)ux + B(x, y)uy + C(x, y)u = 0. (1)
Пусть AC: y = x, BC: y = 1 – x характеристики уравнения (1), а AB – отрезок 0 ≤ x ≤ 1 прямой y = 0.
Пусть далее D ⊂ R2 – конечная область, ограниченная отрезком АВ и при y > 0 – гладкой кривой Г: y = γ(x) расположенная внутри характеристического треугольника ABC, γ(0) = γ(1) = 0.
В качестве задачи Дирихле и Пуанкаре рассмотрим следующие задачи
Задача 1. Найти в области D решение уравнения (1) из класса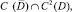 
удовлетворяющее краевым условиям
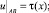
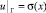(2)
или
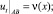
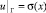, (3)
где
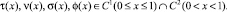
В характеристических координатах ξ = x + y, η = x – y уравнение (1) записывается следующим образом
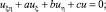(4)
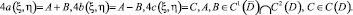
При этом краевые условия (2) и (3) соответственно имеют вид
u(η, η) = τ(η), u(α(η), η) = g(η), 0 ≤ η ≤ 1, (5)
или
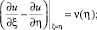
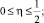
u(α(η), η) = g(η), 0 ≤ η ≤ 1, (6)
где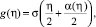 
а функция ξ = α(η) является решением уравнения 
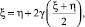при этом
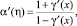
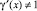, 0 ≤ x ≤ 1.
Пусть, в случае задачи (4), (5), выполняется условие
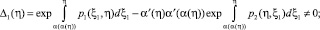(7)
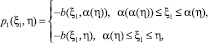
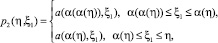
а в случае задачи (4), (6) имеет место
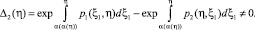(8)
Тогда справедлива
Теорема. Задача 1 однозначно разрешима.
п. 2. Доказательство теоремы. Сначала рассмотрим задачу (4), (5). Используя общее решение уравнения (4) [1] в [3] показано, что решение задачи Коши для уравнения (4) представимо в виде
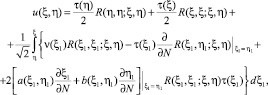(9)
где R(ξ1, η1, ξ, η) – функция Римана уравнения (6), а
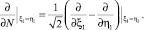
Из (9), при ξ = α(η), используя краевое условие (5), получим интегральные уравнения первого рода
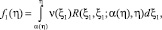0 ≤ η ≤ 1,
где
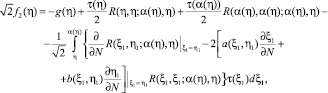
кoторая дифференцированием сводятся к следующему функционально-интегральному уравнению
a1(η)ν(η) + b1(η)ν(α(η)) = μ(η), 0 ≤ η ≤ 1 (10)
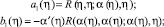
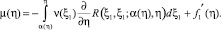
В [4] показано, что, если
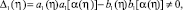(11)
то функциональное уравнение (11) имеет единственное решение вида
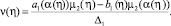(12)
Из определения функции Римана R [1, 5], формула (11) записывается в виде (7), а (12) – в следующем виде
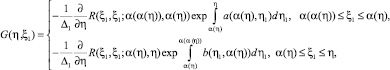(13)
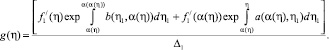
Известно, что функция Римана R по переменным ξ1, η1 и ξ, η имеет такую же гладкость, что и коэффициенты уравнения (4) [5], поэтому ядро G(ξ, ξ1) допускает оценку
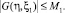(14)
Решение интегрального уравнения (13) будем искать в виде ряда
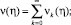(15)
ν0(η) = g(η);
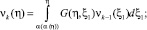k = 1, 2, ... .
Из (14) получим следующие оценки
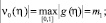
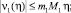
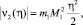
и вообще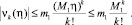 
Тогда, для ряда (15) будем иметь
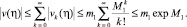
Таким образом, интегральное уравнение (13), (а также (10)), при выполнении условия (7), однозначно разрешимо.
Следовательно, задача (4), (5) имеет единственное решение вида (9), в котором ν(η) находятся из уравнения (13)
Теорема для задачи (1), (2) доказано.
Теперь рассмотрим задачу (1), (3), которая переходит к задаче (4), (6). В этом случае, из (9) при ξ = α(η), с учетом (6), получим следующее функционально-интегральное уравнение
a2(η)τ(η) + b2(η)τ(α(η)) = χ(η), 0 ≤ η ≤ 1, (16)
где
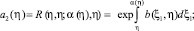
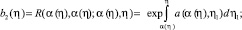
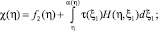
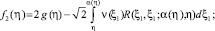
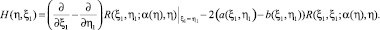
Если выполняется условие
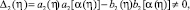
или это тоже, самое условие (8), то функциональное уравнение (16) имеет единственное решение вида
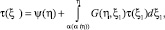
0 ≤ η ≤ 1, (17)
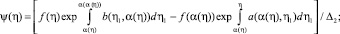
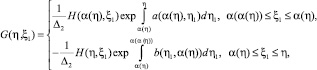
при этом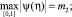 
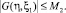
Решение интегрального уравнения (17) будем искать в виде ряда
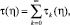
для которого имеет место неравенство
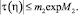
Таким образом, интегральное уравнение (17) (а также (16)), при выполнении условия (8), однозначно разрешимо.
Следовательно, задача (4), (6) имеет единственное решение вида (9), в которой τ(ξ) определяются из уравнений (17).
Отметим, что, если A(x, y) = B(x, y) ≡ 0, то условие (8) не выполняется. В этом случае уравнение (16) имеет вид
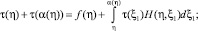(18)
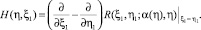
Так как интегральный оператор, стоящий в правой части равенства (18), вполне непрерывен, то, как показано в [4], функциональное уравнение (18) имеет единственное решение.
Таким образом, и в этом случае задача (4), (6) однозначно разрешима.
Теорема для задачи (1), (3) доказана.