Планетарные вибраторы для технологических процессов получили широкое распространение в конструкциях глубинных вибраторов [1]. Метод возбуждения механических колебаний с помощью планетарных вибраторов получил дополнительные области применения при использовании технического решения [2], позволяющего получить направленные колебания.
Целью работы является определение законов изменения перемещения, скорости и ускорения центра масс колебательной системы планетарного вибратора направленных колебаний с заданным соотношением передаточного отношения приводных зубчатых колёс.
Возбуждение механических колебаний в планетарном одновальном вибраторе [2] создаются сателлитом (вибровозбудителем), который обкатывается по неподвижному венцу своей планетарной шестерней, причем центр масс колебательной системы располагается на делительной окружности планетарной шестерни. В такой конструкции вибратора траектория движения центра масс зависит от соотношения диаметров планетарной и венцовой шестерен, а значит, от этого соотношения зависит и характер колебаний.
Для определения характера колебаний, скоростей, ускорений подвижных элементов механизма и возбуждающей силы необходимо знать закон движения центра масс вибровозбудителя, расположенного на делительной окружности планетарной шестерни. Составим расчетную схему (рис. 1).
При работе вибровозбудителя планетарная шестерня (1) сателлита обкатывается по венцовой шестерне (2) корпуса вибратора [3]. В исходном положении центры венцовой шестерни (О1), планетарной шестерни (О2), и водило (3) О1О2 располагаются вдоль оси Y, причем начальная точка (S), принадлежащая венцовой шестерне, совпадает с точкой касания планетарной шестерней (А/) и положением центра масс сателлита (А) (рис.1а). При повороте водила (3) на произвольный угол α, планетарная шестерня поворачивается без скольжения на угол β, а точки А и А/ занимают новое положение (рис. 1б).
а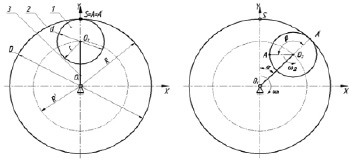 
б
Рис. 1. Схема к определению характера колебаний планетарного вибратора: а – начальное положение механизма; б – произвольное положение
Движение центра масс вибровозбудителя (т. А) является сложным и складывается из относительного вращения шестерни вокруг своей оси (т. О2) и переносного вращения оси планетарной шестерни вокруг оси вибратора (т. О1) [4]. Поэтому закон движения центра масс может быть записан в виде:
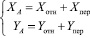(1)
Учитывая, что
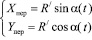
и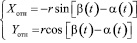 
,
получим:
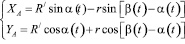(2)
Отметим, что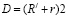 
и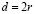 
.
Введем понятия:
коэффициент отношения радиусов
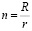(3)
и коэффициент отношения диаметров
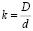(4)
Т.к. планетарная шестерня вращается без проскальзывания, то длина дуги SA/ равна длине дуги АА/ (рис. 1), т.е.
.
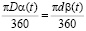Преобразуя это выражение, получим:
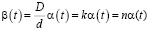. (5)
Из уравнения (3), учитывая что,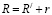 
получим:
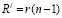. (6)
Преобразуя зависимости (2) с учетом уравнений (5) и (6) получим:
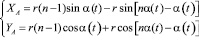
или уравнения движения центра масс вибровозбудителя имеют вид:
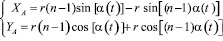(7)
Дифференцируя зависимости (7), получим закон изменения скорости центра масс вибровозбудителя:
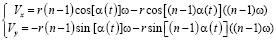(8)
Дифференцируя зависимости (8), получим закон изменения ускорения центра масс вибровозбудителя:
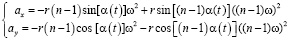(9)
Обрабатывая для различных значений коэффициента отношения радиусов зависимости (7), (8) и (9), (например, с помощью электронной таблицы Excel), получаем траектории движения центра масс (рис. 2), а также графики зависимости* от угла поворота α(t) скорости (рис. 3) и ускорения (рис. 4) центра масс вибровозбудителя.
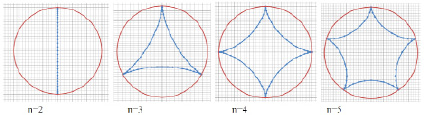
Рис. 2. Траектория движения центра масс вибровозбудителя при различных значениях коэффициента отношения радиусов
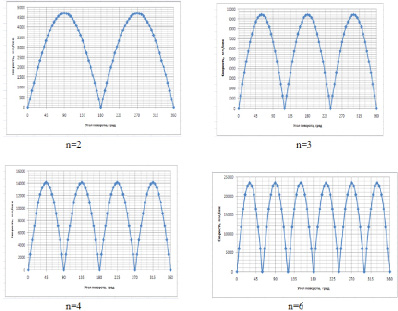
Рис. 3. Зависимость скорости движения центра масс вибровозбудителя от угла поворота α(t) при различных значениях коэффициента отношения радиусов *при построении графиков были приняты значения: r =15 мм, ω =157,08 рад/с
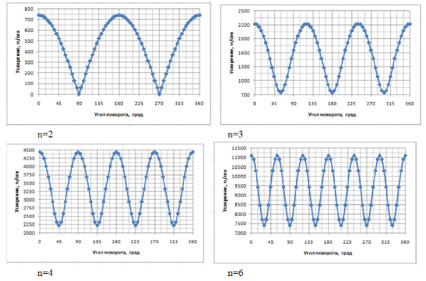
Рис. 4. Зависимость ускорения центра масс вибровозбудителя от угла поворота α(t) при различных значениях коэффициента отношения радиусов
Из рисунков видно, что траектории представляют собой эпициклоиды [1], причем количество вершин соответствует коэффициенту соотношения радиусов. Кроме того количество и положение экстремумов графиков скоростей и ускорений соответствует количеству и положению точек касания центром масс окружности венцовой при обкатывании планетарной шестерни вибровозбудителя.
Т.о. зная ускорения центра масс вибровозбудителя легко можно определить возбуждающую силу вибратора:
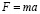, (10)
где m – масса вибровозбудителя (сателлита), кг; а – ускорение центра масс вибровозбудителя (сателлита), м/с2.
Работа выполнена в рамках НИР № 7.3783.2011.