Эффективное проектирование и обеспечение безопасной эксплуатации различных технических объектов требует точного знания величины показателей сопротивления усталости материалов для назначения допустимых эксплуатационных нагрузок и объективной оценки остаточного ресурса [1-3]. В то же время высокая чувствительность показателей сопротивления усталости к действующим факторам, одним из которых является частота циклического нагружения (ω), делает задачу прогнозирования поведения материала при циклическом нагружении значительно более сложной, чем, например, в случае действия постоянной нагрузки [3-9].
Поэтому, целью представленной работы является разработка ускоренного метода прогноза параметров сопротивления усталости металлических материалов с учетом частоты циклического нагружения, на основе ранее полученных нами экспериментальных данных.
За показатели сопротивления усталости были приняты наклон левой ветви кривой усталости (tgαw) и количественное значение повреждаемости поверхности (Ф) материалов [10-11].
В ряде случаев частота циклов нагружения (ω) оказывает существенное влияние на показатели сопротивления усталости [12-20]. Установлено, что увеличение частоты циклов нагружения и в дополнение к этому смягчение схемы напряженного состояния (деформация изгиба вращающихся образцов) приводит к заметному уменьшению наклона левой ветви кривой усталости (параметра tgαw), то есть к улучшению сопротивления усталости. Улучшение параметра сопротивления усталости (tgαw) связано с повышением упрочняемости материала поверхностных слоев образцов (деталей), что снижает усталостную повреждаемость собственно поверхности (Ф) [21-24].
Проведенные исследования позволили получить новые характеристики, определяющие прочность и долговечность образцов (деталей) [25-30]. Экспериментальные данные обрабатывались таким образом, что при ω = const определялись средние значения tgαw, затем строились зависимости tg aw = f(ω). Компьютерная обработка результатов показала, что данные по первой группе укладываются на прямую (рис. 1, а), а по второй – описываются некоторой кривой (рис. 1, б).
а б
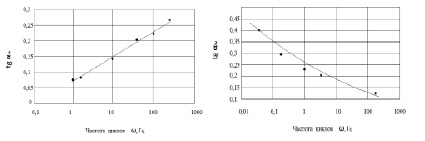
Зависимость показателя сопротивления усталости tgαw от частоты циклов нагружения (ω): а – первой группы материалов; б – второй группы материалов
В первом случае наблюдается ухудшение сопротивления усталости с увеличением параметра ω, а во втором случае – его улучшение. Однако, надо иметь в виду, что параметр tgαw напрямую связан с повреждаемостью поверхности (Ф), и в обеих группах чистых металлов и сплавов рост показателя (Ф) приводит к увеличению tgαw [11 – 12]. Были получены математические зависимости вида:
tgαw=0,0356 ln ω + 0,065 по первой группе материалов;
tgαw=0,262 ω-0,1301 по второй группе материалов.
На основе полученных экспериментальных данных разработан метод прогнозирования прочности и долговечности конструкционных материалов. Зная частоту циклического нагружения, по рис. 1. определяем показатель сопротивления усталости tgαw. В результате получаем два значения параметра tgαw для 1-й и 2-й группы материалов. Используя значения tgαw и зависимость этого показателя от параметра χ, полученную при экспериментальных исследованиях, снимаем два значения параметра
,
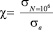где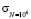 
– напряжение, соответствующее долговечности N=106 циклов.
Данные на однократный разрыв образцов дают возможность знать предел прочности (σв) и уточнить показатели χ и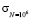 
. Используя графические зависимости tgαw – 
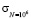можно построить левую ветвь прогнозируемой кривой усталости. Далее находим точку излома прогнозируемой кривой усталости, воспользовавшись работой [4].
Таким образом, получаем экспресс-метод ускоренного построения кривой усталости образцов конструкционного материала, когда есть величина частоты циклического нагружения (ω) и предела прочности материала (σв). Подобным образом можем спрогнозировать кривую усталости требуемой детали и тем самым значительно сэкономить время и стоимость их производства, а особо ответственные детали испытывать с учетом этого прогноза.