1. Постановка задачи и результат. Пусть 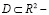 конечная область, ограниченная отрезком
конечная область, ограниченная отрезком 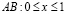 оси
оси 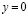 , а при
, а при 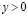 – отрезком
– отрезком
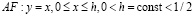 ,
,
гладкой кривой 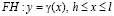 вдоль которой
вдоль которой
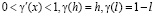
и прямой 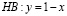 .
.
В области D рассмотрим линейные гиперболические уравнения
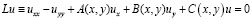 , (1)
, (1)
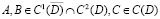 .
.
В качестве краевой задачи с отходом от характеристики рассмотрим следующую
Задача 1 Найти в области D решение уравнения (1) из класса 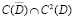 удовлетворяющие краевым условиям
удовлетворяющие краевым условиям
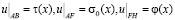 , (2)
, (2)
или
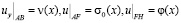 , (3)
, (3)
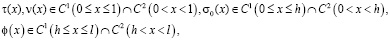
которая встречается при исследовании трансзвуковых проблем [1].
В характеристических координатах 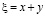 ,
, 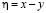 , уравнение (1) записывается следующим образом.
, уравнение (1) записывается следующим образом.
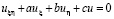 , (4)
, (4)
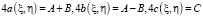 .
.
При этом краевые условия (2) и (3) соответственно имеют вид
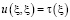 ,
, 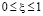 ,
, 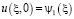 ,
,
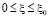 , (5)
, (5)
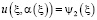 ,
, 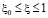 ,
,
или
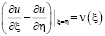 ,
, 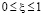 ,
, 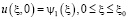 ,
,
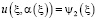 ,
, 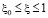 , (6)
, (6)
где
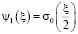 ,
, 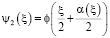 ,
,
а функция 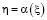 является решением уравнения
является решением уравнения 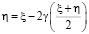 , при этом
, при этом
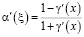 ,
, 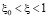 ,
, 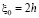 .
.
Пусть в случае задачи (4), (5) выполняется условие
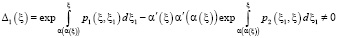 ,
, 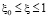 , (7)
, (7)
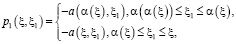
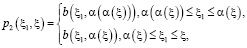
а в случае задачи (4), (6) имеет место
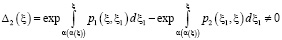 ,
, 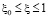 . (8)
. (8)
Тогда справедлива теорема. Задача 1 однозначно разрешима.
2. Доказательство теоремы. Сначала рассмотрим задачи (1), (2), которое переходит к задаче (4), (5). Используя общее решение уравнения (4) [2] в [3] показано, что решение задачи Коши для уравнения (4) представимо в виде
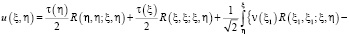
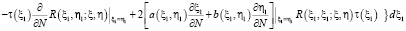 ,(9)
,(9)
где 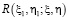 – функция Римана уравнения (4),
– функция Римана уравнения (4), 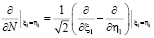 .
.
Тогда, из (9), при h=0 и 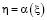 , с учетом (5), получим следующие интегральные уравнения первого рода.
, с учетом (5), получим следующие интегральные уравнения первого рода.
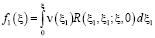 ,
, 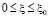 ,
,
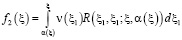 ,
, 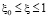 ,
,
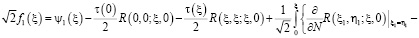
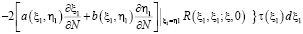 ,
,
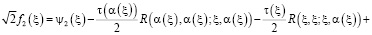
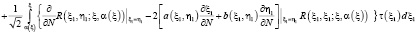 ,
,
которые дифференцированием сводятся соответственно к интегральному уравнению Вольтерра второго рода
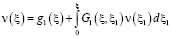 ,
, 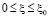 , (10)
, (10)
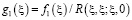 ,
, 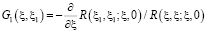 ,
,
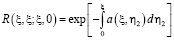 ;
;
и функционально-интегральному уравнению
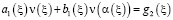 ,
, 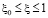 , (11)
, (11)
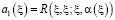 ,
, 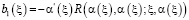 ,
,
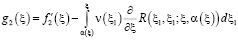 .
.
В [4] показано, что если
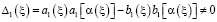 ,
, 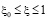 , (12)
, (12)
то функциональное уравнение (11) имеет единственное решение вида
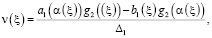
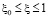 . (13)
. (13)
Из определения функции Римана R [2, 5] формула (12) записывается в виде (7), а (13) в следующем виде
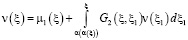 , (14)
, (14)
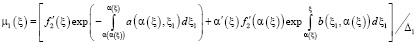 ,
,
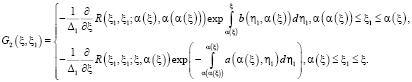
Известно, что функция Римана R по переменным ξ1, η1 и x, h имеет такую же гладкость, что и коэффициенты уравнения (4) [2, 5], поэтому ядро 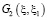 допускает оценку
допускает оценку
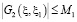 . (15)
. (15)
Решение интегрального уравнения (14) будем искать в виде ряда
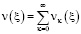 , (16)
, (16)
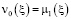 ,
,
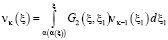 ,
,
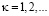
Из (15) получим следующие оценки
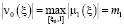 ,
,
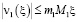
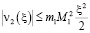 ,
,
и вообще 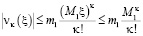 .
.
Тогда для ряда (16) будем иметь
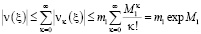 .
.
Таким образом, интегральное уравнение (14), (а также (11)), при выполнений условия (7) однозначно разрешимо.
Следовательно, задача (4), (5) имеет единственное решение вида (9), в которой n(x) определяются из (10) и (14).
Теорема для задачи (1), (2) доказана.
Теперь рассмотрим задачу (1), (3) , которая переходит к задаче (4), (6). В этом случае из (9) при h=0 и 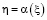 , с учетом (6), получим следующие интегральное уравнение Вольтерра второго рода
, с учетом (6), получим следующие интегральное уравнение Вольтерра второго рода
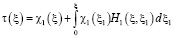 ,
, 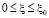 , (17)
, (17)
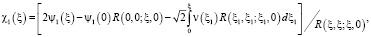
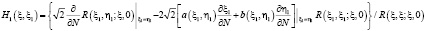
и функционально – интегральное уравнение вида
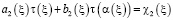 ,
, 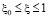 , (18)
, (18)
где
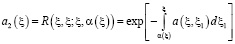 ,
,
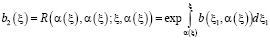 ,
,
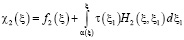 ,
,
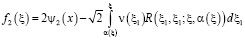 ,
,
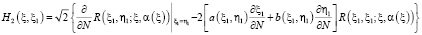 .
.
Если выполняется условие
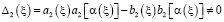 ,
,
или это то же самое условие (8), то функциональное уравнение (18) имеет единственное решение вида
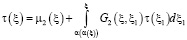 , (19)
, (19)
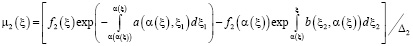 ,
,
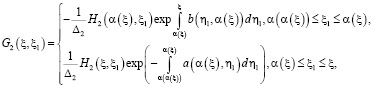
при этом
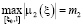 ,
, 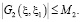
Решение интегрального уравнения (19) будем искать в виде ряда 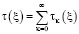 для которого имеет место неравенство
для которого имеет место неравенство 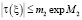 .
.
Таким образом, интегральное уравнение (19) (а также (18)), при выполнении условия (8) однозначно разрешима.
Следовательно, задача (4), (6) имеет единственное решение вида (9), в которой t(x) определяются из (17) и (19).
Отметим, что если 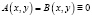 , то условие (8) невыполнимо. В этом случае уравнение (18) имеет вид
, то условие (8) невыполнимо. В этом случае уравнение (18) имеет вид
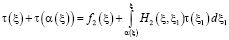 ,
, 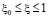 , (20)
, (20)
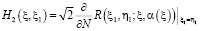 .
.
Так как интегральный оператор, стоящий в правой части равенства (20) вполне непрерывен, то как показано в [4] функциональное уравнение (20) имеет единственное решение.
Таким образом и в этом случае задача (4), (6) однозначно разрешима .
Теорема для задачи (1), (2) доказана.

