В условиях финансово-экономического кризиса предприятия и управляющие органы региона сталкиваются с проблемами определения приоритетов промышленного развития регионов, поиска ресурсов для обеспечения такого развития, и, в первую очередь, инвестиционного ресурса. Получение инвестиционного ресурса зависит от множества факторов политического, экономического, географического характера. К наиболее важным факторам следует отнести уровень инновационности предполагаемых направлений развития, наличие современной (децентрализованной) структуры управления региональным экономическим развитием и современных (корпоративных) методов управления предприятиями перспективных отраслей.
Решение задачи оптимального распределения инвестиционного ресурса целесообразно осуществлять на основе следующей системной концепции. Выраженные в стоимостном виде материальные и финансовые потоки экономических агентов социально-экономической системы (СЭС) учитывают как стратегические (прибыль, инвестиции), так и тактические (выручка от продажи продукции, амортизация, фонд оплаты труда, налоги, оборотные затраты, кредиты, дотации и пр.) их доходные и расходные составляющие. Это позволяет задавать производственную функцию системы алгоритмически, выделяя и максимизируя ее стратегические доходные и расходные составляющие, и, вместе с тем, за счет использования универсального (в смысле независимости от рода производственной деятельности) алгоритма начисления прибыли производственного сектора, достаточно подробно учесть микроэкономические особенности деятельности экономических агентов СЭС.
В данной работе кратко описано разработанное математическое и программное обеспечение поддержки принятия решений при управлении инвестиционными проектами региональной экономики. Полученные результаты позволяют осуществлять эффективное распределение общих ресурсов (труд, капитал, инвестиции) между конкурентоспособными предприятиями, отраслями, регионами, решать задачи оптимального управления экономическим развитием региона в целом. Это дает возможность региональному центру повышать обоснованность принятия решений, гибкость и адаптивность при управлении региональным экономическим развитием.
В работе [6] приведена многокритериальная математическая модель распределения инвестиций в выбранные n направлений экономического развития региона, позволяющая находить оптимальный уровень производства продукции и инвестиций в основные производственные фонды с учетом интересов трех экономических агентов (производителя, потребителя и управляющего органа). При реализации получаемого оптимального плана обеспечивается нахождение Парето-точек критериального пространства решений, позволяющее указанным экономическим агентам принимать обоснованные решения по согласованию своих интересов.
Суть описываемого подхода к созданию системы поддержки принятия решений при управлении региональным экономическим развитием можно изложить в виде следующих этапов.
Этап 1. Задать основные технико-экономические характеристики (количество, стоимость, производительность и срок службы производственного оборудования, объектов недвижимости, цену продажи произведенной на них продукции) реальных производственных активов, необходимых для эффективного функционирования конкурентоспособных направлений экономической деятельности региона, выбранных для поддержки региональным управляющим центром. Оценить основные производственные (выручка и затраты), инвестиционные (капитальные вложения в строительство, приобретение основных и оборотных средств, покупка ценных бумаг и т.п.) и финансовые (дотации производственному и потребительскому секторам, налоги, кредиты, займы, выпуск ценных бумаг и т.п.) денежные потоки экономических агентов. Следует отметить, что, несмотря на то, что для каждого региона источники доходов и затрат имеют свою, часто существенно различающуюся в стоимостном выражении структуру, указанные выше характеристики можно найти на официальных сайтах экономической статистики регионов.
Этап 2. Рассмотреть основные ограничения при функционировании региональной социально-экономической системы (безубыточность производственного сектора, платежеспособность производителя и потребителя, ограничения на объем инвестиций, дотаций, спрос на продукцию и т.п.). При этом следует отметить, что спрос на продукцию в условиях децентрализованной экономики является не только основным экономическим ограничителем, но и основным стимулом производства продукции и услуг в соответствии с принципом «спрос рождает предложение».
Этап 3. Задать целевую функцию региональной социально-экономической системы (в зависимости от количества, интересов его участников) с учетом возникающих при его реализации рисков. Заметим, что при реализации долгосрочных, стратегических инвестиционных проектов структура денежных потоков должна отражать потоки, соответствующие как быстроликвидным, так и малоликвидным статьям конечного состояния совокупного производителя и совокупного потребителя (их добавленной стоимости). Из этого, в частности, следует необходимость учета на последних стадиях реализации инвестиционных проектов с высокой общественной значимостью остаточной стоимости материальных и нематериальных активов, заключенных контрактов и прав собственности как предприятий, так и населения региона. Эта особенность должна учитываться в структуре целевых функции участников регионального экономического процесса, которые, в общем случае, состоят из двух слагаемых – денежных (быстроликвидных) средств и остаточной стоимости основных фондов (малоликвидных средств), причем во всяком случае максимизируются именно их суммы. Следует отметить, что в различные периоды реализации инвестиционных проектов интересы участников могут иметь существенно различную направленность. В этой связи горизонт планирования ИП может быть разделен на несколько связанных между собой последовательно или параллельно временных этапов, а общая задача оптимального управления решается как задача оптимизации на общем горизонте планирования.
Этап 4. Записать полученные соотношения в виде классической дискретной многокритериальной задачи оптимального управления:
уравнения движения:
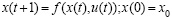 , (1)
, (1)
ограничения
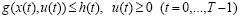 , (2)
, (2)
целевая функция
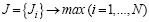 , (3)
, (3)
где x(t) – вектор неуправляемых параметров (фазовый); u(t) – вектор управляемых параметров (управляющий); F(t), f(t), g(t), h(t) – соответственно заданные функции цели, уравнений движения и ограничений задачи, T0 – горизонт планирования, N – количество критериев. При этом составляющие Ji целевой функции имеют следующий структурный вид:
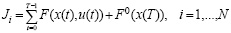 .
.
В качестве экономических агентов, имеющих свой целевой критерий при анализе регионального экономического развития, целесообразно рассматривать, как минимум, обобщенного производителя, обобщенного потребителя, региональный управляющий орган, при необходимости дополняя их блоками функционирования финансового и/или коммерческого сектора.
Этап 5. Выбор метода решения и получение оптимальных параметров экономического процесса. Динамические задачи оптимального управления вида (1)-(3) могут решаться с помощью алгоритмов, основанных на оптимизационных принципах Беллмана и Понтрягина. Для получения субоптимальных решений можно применять генетические алгоритмы [2, 3]. Если все функции F(t), f(t), g(t), h(t) являются линейными, то задача (1)-(3) превращается в многокритериальную, многошаговую задачу линейного программирования (ММЗЛП) с фиксированным начальным состоянием. С помощью z-преобразования [7, 8] они превращаются в свои статические аналоги, которые сохраняют фундаментальные свойства исходных. Основными интегральными ограничениями деятельности региональной социально-экономической системы выступают спрос на произведенную продукцию, ограниченность фондоотдачи ОПФ, а также неотрицательность денежных потоков производственного и потребительского секторов. Построенная задача с достаточной для практики точностью и адекватностью способна описывать функционирование региональных экономических систем и прогнозировать стратегию их развития. Линейность указанной задачи позволяет разрабатывать модели деятельности не только региональных социально-экономических систем, но и систем микро- [7] и макроуровня [12], а также эффективные алгоритмы их теоретического и численного анализа [9-11] с выходом на создание многофункциональных систем поддержки принятия решений [1, 13].
Технология построения информационных услуг
На основе предложенного подхода создана система поддержки и принятия решений для предварительной оценки региональных инвестиционных проектов, состоящая из совокупности математических моделей, алгоритмов их анализа, пакета прикладных программ автоматизированной обработки экономической информации. Отметим, что, на основе указанного подхода, разработан пакет программ [5], позволяющий пользователю-математику в визуальном режиме создавать и корректировать математические модели в форме многокритериальных задач линейного программирования, а экономисту-аналитику – в удобном режиме заносить входную статистическую информацию и представлять в виде графиков многопараметрических зависимостей и Парето-множеств, исходя из его потребностей. Данный программный пакет предусматривает 2 режима работы – 1) конструктор моделей и 2) автоматизированное рабочее место аналитика, краткое описание которых приводится ниже.
Конструктор моделей
При решении одно- и многошаговых задач оптимального управления вида (1)-(3) затруднено занесение матричной информации, в первую очередь, из-за отсутствия наглядности. Конструктор моделей позволяет создавать пользовательские модели в визуальном режиме, добавляя модельные параметры, а также редактируя векторно-матричную информацию, имея перед глазами образ матрицы (рис. 1). Кроме того, в пакете также имеется отладчик, позволяющий обнаруживать ошибки или противоречия в занесении числовой информации модели (рис. 2). Отметим при этом, что занесение информации требует знания лишь базовых навыков владения компьютером.
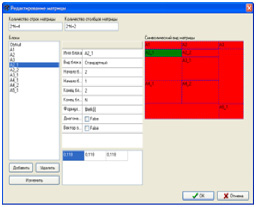
Рис. 1. Редактор матриц
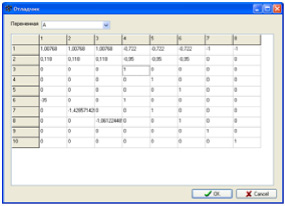
Рис. 2. Отладчик
Автоматизированное рабочее место (АРМ) аналитика
В этом режиме исследователь, после внесения численной информации из предметной области, на выходе получает результаты расчета, а также возможности их графического анализа. Данный режим работы предъявляет минимальные требования к пользователю – владение информацией о содержательном смысле числовых параметров модели. Поэтому в данном режиме могут работать студенты или специалисты с минимальным базовым набором знаний и навыков по предметной области. Пример окна интерфейса работы в данном режиме приведен на рис. 3. Кроме того, возможно построение графиков зависимостей в модели, что позволяет установить визуально характер зависимости и извлечь дополнительные сведения из модели.
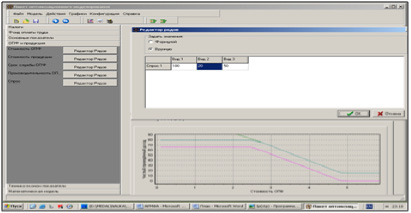
Рис. 3. Окно интерфейса АРМ аналитика
К основным преимуществам созданного программного обеспечения, на наш взгляд, следует отнести:
1. Возможность создания математической модели в пользовательском режиме
2. Наличие анализатора математическ;их формул;
3. Визуальный редактор матриц, заданных в виде блоков формул;
4. Возможность разделения параметров модели по группам;
5. Возможность защиты данных модели от несанкционированного доступа;
6. Возможность добавления описания модели;
7. Гибкая настройка пользовательского интерфейса;
8. Система компиляции математических выражений;
9. Высокая скорость расчета;
10. Поддержка динамически загружаемых математических ядер, что позволяет пользователю выбрать способ решения. (Например, библиотека с реализацией симплекс-метода и библиотека с реализацией решателя с помощью генетических алгоритмов). Данная архитектура позволяет разрабатывать математическое ядро сторонним разработчикам;
11. Встроенная система шифрования Blowfish;
12. Интуитивно понятный пользовательский интерфейс;
13. Построение неограниченного количества графиков и Парето-множеств по любым параметрам модели;
14. Гибкая настройка вида графиков (легенда, метки, значения в точках).
При вводе-выводе информации используется оригинальный быстродействующий графический анализатор функций [4], позволяющий эффективно обрабатывать многопараметрические функции.
В настоящее время описанная система поддержки принятия решений инвестиционного аналитика развивается в направлении конечного пользователя – экономиста, финансиста, организатора бизнеса, регионального управляющего центра и т.п. Соответствующий пакет прикладных программ используется при расчете ряда инвестиционных проектов стратегического планирования, купли-продажи и реструктуризации бизнеса, развития конкурентоспособных отраслей региональной экономики. Положенные в его основу модели в некоторых частных случаях позволяют рассчитывать стратегию экономического развития, связанную с функционированием нескольких производственных подразделений конкурентоспособных отраслей в динамике на перспективу до 30 периодов.

