Известно, что структура различных иммунных процессов носит существенно нелинейный, распределенных и стохостический характер, ведущие процессы в большинстве случаев являются билинейными. Если судить по аналогии, то билинейные системы появляются при описании взаимодействие молекул антител с чужеродным веществом.
Анализ биологических систем и управление ими допустимо на основе билинейных моделей, если взаимодействия между составляющими можно будет описать с помощью временных линейнных уравнении, принимающих значения из некоторого множества и определяющих действие иерархии. В данной работе рассмотрена система на основе билинейных моделей. Биологическая система требует преодоления жестких ограничении, связанных с требованиями линейности. Другая ее особенность-эта изменчивая структура. Эта свойства является важным в тех случаях, когда на управления накладывается ограничения.
Лемма. Управления вида
осуществляет стабилизацию движения системы:
;
.
Доказательства данной леммы можно найти [1, 2, 3].
Постановка задачи. Выбором управления 
требуется стабилизировать движения на конечном отрезке времени.
Пусть 
тогда стабилизирующее управление можно предоставить в виде:
Для решения поставленной задачи взят процесс управления периодическим течением болезни [4, 5]. Этот процесс может быть описан:
,
,
с начальными условиями: 
; :
; :
,
где первое уравнение описывает концентрацию зрелых плазмацитов, второе уравнение концентрацию антигена третье уравнение описывает концентрацию антител [6, 7].
Используем линеаризованную систему данной модели, которой получаем, пренебрегая членами x2x3.
Тогда матрица системы имеет вид:
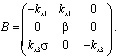
Теперь вычислим собственные значения матрицы:
Как видно решения неустойчивое и мы рассматриваемой модели добавляем стабилизирующее управления на 
конечном отрезке: 
Фундаментальная матрица определяется из уравнения:
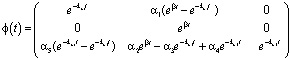
Теперь вычислим
Тогда имеем
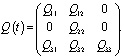
После вычислим элементы матрицы:
Далее находим
Таким образом, решение рассматриваемой системы при стабилизирующем управлении имеет вид:
А стабилизирующее управление имеет вид:
Эти найденные выражения определют программное управление. Кроме этого, мы задачу исследовали с помощью численных методов.
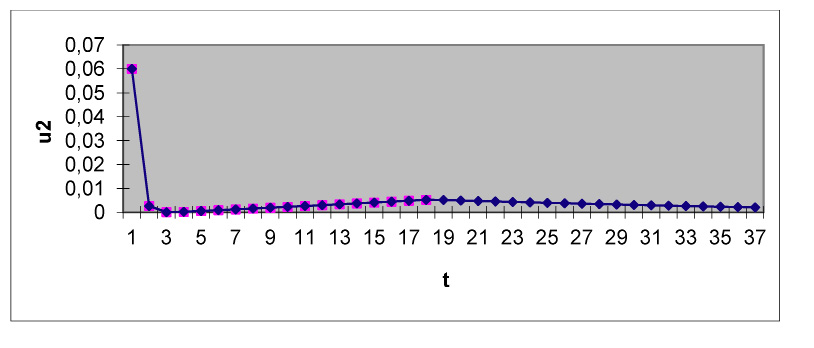
Изображение поведения управления u2 при 1,70<х1<1,89 , 5.1<х2<3.2, 0.9< х3<6.5
Рисунок показывает изменение поведения управления, в частности, u2. Именно u2 заменяет билинейность во втором уравнении системы моделируемого процесса. Как видно, в начальный момент времени значении u2 резко падает и даже достигает нулевого значения. Затем, через два часа, опять восстановливает свое значение и так плавно приближается к нулю.
Заключение. Оценку близости аппроксимационной модели можно получить, выбирая продолжительность времени 
. Таким образом, мы можем приближенно находить решение билинейной системы через решения линеаризованной системы, обеспечивающее стабилизацию системы на конечном отрезке времени.