Большую часть срока службы космического аппарата (КА) находится на большой высоте, при свободномолекулярных условиях и экспериментальное исследование таких условиях довольно проблематично. Поэтому методы вычислительной аэродинамики разреженного газа в настоящее время являются практически единственным средством получения информации об аэродинамической обстановке около космического аппарата на больших высотах. Особенности исследований высотной аэродинамики связаны с тем, что при проектировании и эксплуатации КА необходимо рассчитывать аэродинамические характеристики (АДХ) в широком диапазоне изменения определяющих параметров (высоты полета, параметров атмосферы, скорости полета, ориентации КА, геометрических параметров модели КА и т. п.).
Определение граничных условий на обтекаемых разреженным газом поверхностях является одной из важнейших проблем кинетической теории газов [1]. Взаимодействие газа с поверхностью обтекаемого тела играет определяющую роль в высотной аэродинамике [2].
Проявление методов статистического моделирования (Монте-Карло) в различных областях прикладной математики связано с необходимостью решения качественно новых задач, возникающих из потребностей практики. Метод прямого статистического моделирования является наиболее распространенным среди численных методов решения прикладных задач динамики разреженного газа. Метод Монте-Карло широко применяется в аэродинамике как универсальный метод расчета тел сложной формы с учетом затенения и многократных соударений с поверхностью отраженных частиц. Более того, тенденции применения этого метода к расчету всего спектра течений – от сплошной среды до свободномолекулярного течения [3, 4].
Целью настоящей работы является исследование АДХ КА методом прямого статистического моделирования (Монте-Карло) в высокоскоростном потоке разреженного газа. В работе рассматриваются различные модели взаимодействия молекул газа с поверхностью и их влияние на АДХ.
Методика решения задач высотной аэродинамики (метод прямого статистического моделирования (Монте-Карло))
Важным преимуществом метода прямого статистического моделирования по сравнению с решением задачи на основе уравнения Больцмана является формулировка граничных условий в терминах вероятностного описания для каждой молекулы, а не в виде функции распределения в окрестности границы [3-5]. Будем считать, что на границах области столкновения молекул между собой не играют существенной роли, что справедливо в случае Kn >> 1, т.е. когда длина пробега существенно превышает размеры тела. Тогда на границах области функцию распределения влетающих в область молекул можно положить равной f∝.
Далее необходимо вычислить количество частиц, влетающих в область в единицу времени через все границы:
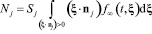 ,
,
где Nj – поток частиц через границу с номером j. nj – единичный нормальный вектор. Вычисление Nj сводится к известным интегралам от максвелловской функции, зависящим от скоростного отношения 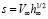 ,
, 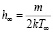 .
.
На первом этапе разыгрывается номер границы, через которую влетает очередная частица. В случае высокоскоростного потока алгоритм может быть упрощен: если поперечные размеры расчетной области достаточны для учета теплового разброса скоростей молекул, влет молекул можно рассматривать только с передней границы.
На втором этапе необходимо определить координату влета частицы. Так как поток газа однороден, координаты молекул равномерно распределены по соответствующей части границы.
На третьем этапе по известным соотношениям, описанным выше, вычисляется скорость молекулы как случайная величина, распределенная в соответствии с функцией f∝.
На четвертом этапе, зная координаты точки влета молекулы и ее скорость, определяются координаты точки попадания этой молекулы на тело (если молекула попадает на тело). Вычисляются величины импульса и энергии, приносимые молекулой на тело.
На пятом этапе по функции распределения отраженных молекул определяется скорость отраженной молекулы и вычисляется реактивный импульс и энергия, уносимая отраженной молекулой. Вычисляя средние величины импульса и энергии по большому количеству молекул, находим силы и моменты, действующие на летательный аппарат, а также потоки энергии, приносимые газом на поверхность летательного аппарата.
Алгоритм метода Монте-Карло выглядит следующим образом:
- Ввод данных
- Определение номера части границы;
- Вычисление координат точки влета частицы в область;
- Вычисление скорости частицы;
- Вычисление координаты точки пересечения траектории частицы с поверхностью тела;
- Вычисление импульса и энергии, приносимых частицей;
- Вычисление скорости отраженной частицы;
- Вычисление импульса и энергии отраженной частицы.
- Выполнение пп. 4-7 до покидания молекулой расчетной области.
- Осреднение данных.
Так как частицы не сталкиваются между собой, отраженная частица покидает расчетную область. В алгоритме происходит передача управления на пункт 1 и вычисляется траектория следующей частицы. Если тело невыпуклое или имеется несколько тел, алгоритм несколько усложняется. После пункта 8 отраженная частица может попасть на другую часть тела, поэтому управление передается на пункт 5, где вычисляются координаты точки пересечения траектории частицы с поверхностью. Если траектория частицы не пересекает тело, частица покидает область и управление передается на пункт 1.
К недостаткам метода можно отнести высокие требования к аппаратным ресурсам, сложность расчета нестационарных течений с макроскопическими скоростями, малыми по сравнению со скоростью звука. Процедура решения задач методом Монте-Карло заключается в том, что физическому явлению или описывающему его уравнению ставится в соответствие некоторый случайный процесс, математическое ожидание которого является оценкой искомых характеристик задачи. Как правило, математическая сложность рассматриваемых в динамике разреженных газов задач позволяет разграничить расчетные методы на регулярные и чисто статистические.
Модели взаимодействия молекул газа с поверхностью
Роль законов взаимодействия молекул с поверхностью проявляется тем сильнее, чем газ разрежен [1]. Граничным условиями для уравнения Больцмана являются условия, ввязывающие функцию распределения падающих и отраженных молекул.
В модели Максвелла плотность распределения отраженных молекул имеет вид
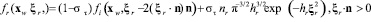 ,
,
и ядро рассеяния [1, 2] имеет вид
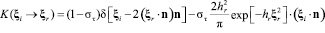 ,
, 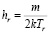 .
.
Здесь полагается, что доля (1 – σt) молекул отражается зеркально, а остальная часть σt молекул – диффузно, параметр 0 ≤ σt ≤ 1 определяет коэффициент аккомодации касательной компоненты импульса σt = (Pτi –Pτr)/Pτi.
Компоненты вектора скорости при диффузном отражении моделируются в локальной сферической системе координат, ось которой направлена вдоль вектора внешней нормали к поверхности, с помощью выражений [6]
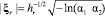 ,
, 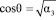 ,
,
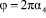 ,
,
где α1, α2, α3, α4 – независимые случайные числа, равномерно распределенные в интервале (0, 1), q и j – полярный и азимутальный углы.
Выражение для скорости отраженной молекулы с учетом неполной аккомодации по кинетической энергии имеет вид
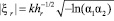 ,
,
где 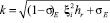 .
.
Коэффициент аккомодации кинетической энергии определяется в виде
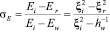 ,
,
здесь Ew – энергия, которую уносили бы отраженные молекулы, если бы газ находился в равновесии со стенкой, т. е. когда Tr = Tw.
К. Черчиньяни и М. Лампис предложили феноменологическую модель (CL), которая также удовлетворяет принципу взаимности и является усовершенствованием максвелловской модели [7]. Модель основана на введении двух параметров, которые представляют собой коэффициент аккомодации σn = sEn по кинетической энергии, связанной с нормальной компонентой скорости, и коэффициент аккомодации касательной компоненты импульса σt. Модель CL хорошо соответствует результатам лабораторных исследований с высокоскоростными молекулярными пучками [2]. Хотя сравнение ограничено лабораторными условиями, модель CL является теоретически обоснованной и относительно простой. Позднее появились модификации ядра рассеяния модели CL [8], однако они дают незначительное улучшение при сравнении с лабораторными экспериментами. В общем случае модель взаимодействия имеет несколько параметров произвольного физического смысла, которые позволяют добиться разумного согласия с результатами лабораторных исследований в некотором диапазоне условий. Универсальная модель должна использовать ядро рассеяния, полученное на основе физического эксперимента в широком диапазоне чисел Кнудсена и скоростей потока [2].
В модели CL ядро рассеяния для нормальной к поверхности компоненты скорости имеет вид
 ;
;
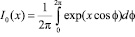 ,
,
здесь I0 – функция Бесселя первого рода, ξni, ξnr – нормальная к поверхности компонента скорости для падающей и отраженной молекул, отнесенная к 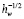
Ядро рассеяния для касательной к поверхности компоненты скорости имеет вид
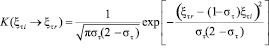 ;
;
здесь ξτi, ξτr – касательная к поверхности компонента скорости для падающей и отраженной молекул, отнесенная к 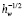 .
.
Ядро рассеяния удовлетворяет принципу взаимности и условиям нормировки:
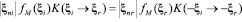 ,
,
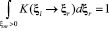 ,
,
здесь fM – Максвелловская плотность распределения.
Использованное преобразование расширяет CL модель для учета обмена вращательной энергией между газом и поверхностью [8]. Модель в таком виде называется моделью Черчиньяни-Лампис-Лорда (CLL). Потом были предложены модификации модели [9] для учета обмена колебательной энергией и расширения диапазона состояний рассеянных молекул. Модель CLL в настоящее время получила широкое признание в работах [10-17].
Результаты расчетов и обсуждение
Рассмотрим приложение описанных методов и моделей к решению задач определения аэродинамических характеристик космических аппаратов в свободномолекулярном потоке разреженного газа. Используются различные модели взаимодействия молекул с поверхностью (Максвелла и Черчиньяни-Лампис-Лорда, CLL). Представлены результаты расчета различным моделями взаимодействия газа с поверхностью (Максвелла и CLL) методом Монте-Карло.
Геометрия тела представлена набором треугольников, к преимуществам такого представления относится простота описания формы тела и простота вычисления аэродинамических характеристик, основным недостатком является негладкость границы тела. Триангуляция поверхности тела и экспорт в формат STL (STereo Litography) были произведены с помощью комплекса автоматизированного проектирования SolidWorks на основании исходной модели, импортированной из формата IGS. Значения параметров: температурный фактор tw = Tw/T∝ = 0.04, 0.1; скоростное отношение s = 20; коэффициенты аккомодации тангенциального импульса и нормальной энергии στ, σn = 0.5, 0.75, 1. Расчет проводился с использованием 5×106 частиц.

Рис. 1. Геометрий крылатого космического аппарата
На рис. 2–4 представлены зависимости коэффициентов силы сопротивления Cx, подъемной силы Cy, момента тангажа mz от угла атаки a от –90° до +90° для крылатого космического аппарата (рис. 1).
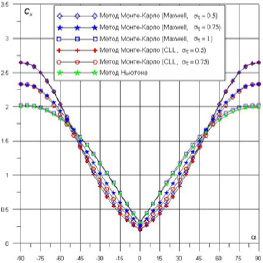
Рис. 2. Зависимости Cx(a) для крылатого космического аппарата (tw = 0.1)
При уменьшении στ от 1 до 0.5 величина Cx снижается до 1.85 при –55° < α < 55°, и при уменьшении στ от 1 до 0.75 величина Cx снижается до 1.74 при –55° < α < 55°. В рамках модели Максвелла при больших по модулю углах атаки зеркально отраженные молекулы повышают величину Cx, чего не наблюдается в рамках модели CLL.
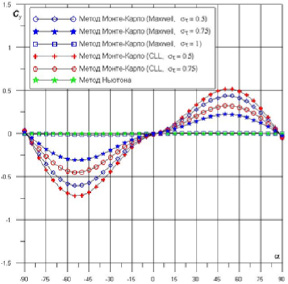
Рис. 3. Зависимости Cy(a) для крылатого космического аппарата (tw = 0.1)
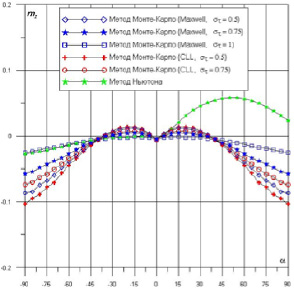
Рис. 4. Зависимости mz(a) для крылатого космического аппарата (tw = 0.1)
При уменьшении στ от 1 до 0.5 величина Cx увеличивается до 2.64 при α = +90°. Коэффициент Cy снижает в несколько раз по модулю при уменьшении στ от 1 до 0.5, 0.75. Зависимость mz(a) объясняет о том, что при понижении στ чувствительно увеличивает в рамках разных диапазонов углов атаки с благоприятными балансировочными свойствами по тангажу.
Можно объяснить что, при нулевой аккомодации все молекулы отражаются зеркально, и полной аккомодации отражаются диффузно. Зеркальные отраженные молекулы передают поверхности больший импульс, чем диффузно рассеянные от холодной стенки молекулы. Можно сказать что, величина нормальных и касательных напряжений, вызываемых отраженным потоком, зависит от характера отражения молекул. При зеркальном отражении pr = pi. Тогда суммарное нормальное напряжение, действующее на элемент поверхности, будет равно p = 2pi. Касательное напряжение τr, вызываемое отраженными молекулами, равно τr = −τi. Поэтому суммарное напряжение трения будет равно нулю t = 0. При диффузном отражении касательное напряжение от отраженных молекул равно нулю, так как при этом все направления отражения являются одинаково вероятными.
Отметим, что близость результатов, полученных с помощью моделей Максвелла и CLL, отмечалась ранее в работе [13] для тел с высокими коэффициентами аккомодации поверхности, что позволяло достигнуть лучшего согласования с результатами эксперимента в аэродинамической трубе [17].
Заключение
Представлены результаты расчетов аэродинамических сил сопротивления Cx, подъемной силы Cy , момента тангажа mz спускаемого аппарата и крылатого космического аппарата методом Монте-Карло при различных значениях коэффициентов аккомодации с использованием различных модели взаимодействия молекул с поверхность. Исследовано влияние на АДХ особенностей модели взаимодействия молекул с поверхностью. Результаты сравнены с традиционным методом Ньютона и достоверны. Разработанные программные системы позволяют оперативно получать АДХ разрабатываемых и эксплуатируемых КА на орбите и на начальном участке траектории спуска и могут быть использованы при проектировании перспективных космических аппаратов.
Работа выполнена при поддержке РФФИ (Грант № 11-07-00300-а).

