Рассмотрим следующую краевую задачу для дифференциального оператора второго порядка с суммируемым потенциалом:
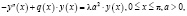(1)
с многоточечными граничными условиями:
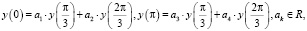(2)
,
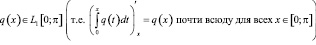на коэффициенты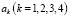 
в дальнейшем будут наложены дополнительные условия.
Методика нахождения асимптотики решений дифференциального уравнения (1) при больших значениях спектрального параметра l в случае суммируемого потенциала q(x) изложена автором в работах [1, 2].
Теорема 1. Пусть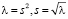 
, причём зафиксируем ту ветвь корня, для которой 
.
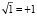Общее решение дифференциального уравнения (1) имеет следующий вид:
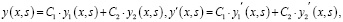(3)
где 
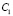и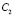 
– произвольные постоянные, при этом линейно независимые решения 
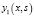и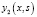 
имеют при 
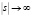следующие асимптотики:
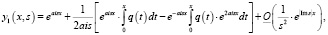(4)
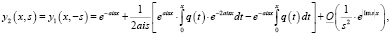(5)
аналогичные формулы справедливы для функци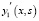й 
и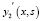 
.
Подставляя формулы (3), (4), (5) в граничные условия (2), приходим к следующему выводу.
Теорема 2. Уравнение на собственные значения краевой задачи (1) – (2) имеет следующий вид
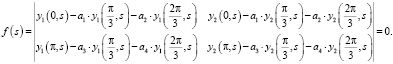(6)
Введем следующую замену:
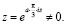(7)
Тогда уравнение (6) с помощью формул (4), (5), (7) принимает вид
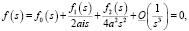(8)
где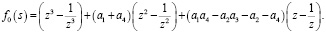 
Основное приближение уравнения (8) представляет собой уравнение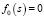 
, которое всегда имеет корн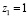и 
и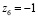 
, и ещё какие-то четыре корня. Очень важный вид граничных условий вида (2) получается в случае
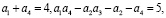(9)
Соотношения (9) наблюдаются очень часто, например, если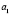 
– любое, 
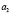– любое 
, 
.
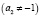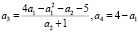В случае (9) уравнение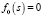 
имеет критические корни:
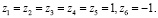(10)
Аналогично работе [3] получаем следующий результат.
Теорема 3. В случае (9) – (10) асимптотику собственных значений краевой задачи (1) – (2) следует искать в следующем виде:
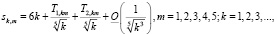
где коэффициенты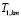 
, 
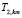зависят от q(x) и могут быть найдены методами работ [1] и [3].