В этой статье изучим спектральные свойства многоточечной краевой задач и для дифференциального оператора четвёртого порядка:
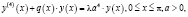(1)
с граничными условиями вида:
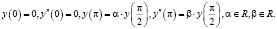(2)
Потенциал q(x) может быть гладким (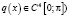
, как это было в работе [1], а может быть интегрируемым на отрезке 
(
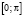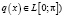, как это было в работе [2]. Основной вопрос нашего исследования: когда будет наблюдаться эффект «расщепления» кратных в главном собственных значений дифференциального оператора (1) – (2)? Этот эффект впервые был отмечен и изучен автором в работе [3]. Пусть 
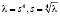, причем для корректности наших дальнейших вычислений зафиксируем ту ветвь арифметического корня, для которой 
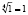. Пусть 
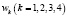– различные корни четвёртой степени из единицы:
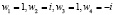, при этом 
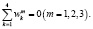(3)
Основное приближение краевой задачи (1) – (2) получается при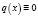 
. В этом случае решение дифференциального уравнения (1) имеет следующий вид:
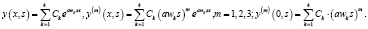(4)
Подставляя формулы (4) в первые два из условий (2), получим формулу:
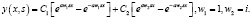(5)
Подставляя формулу (5) в граничные условия (3) получаем следующее утверждение.
Теорема 1. Уравнение на собственные значения краевой задачи (1) – (2) имеет вид:
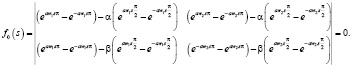(6)
Произведя замену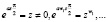 
, уравнение (6) можно привести к виду:
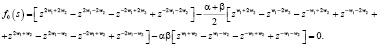(7)
Индикаторная диаграмма (см. [4, глава 12]) уравнение (7) представляет собой квадрат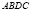 
с вершинами 
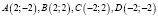, при этом на сторонах квадрата лежат точки 
.
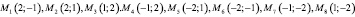Все эти точки влияют на асимптотику корней уравнения (7) (т.е. влияют на асимптотику собственных значений краевой задачи (1) – (2)).
Самый интересный эффект наблюдается в случае, если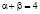 
(т.е. α – любое действительное число, 
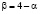). В этом случае после замены 
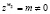уравнение на собственные значения перепишется (для сектора 
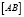) в виде:
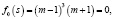(8)
т.е. оно имеет корни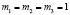 
(кратность корня равна 3) и 
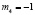(кратность 1).
Теорема 2. В случае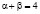 
асимптотика собственных значений краевой задачи (1) – (2) имеет вид:
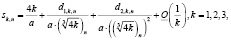(9)
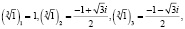коэффициенты 
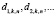выписываются в явном виде в зависимости от потенциала q(x).