Рассмотрим следующее дифференциальное уравнение второго порядка с запаздывающим аргументом с гладкой весовой функцией:

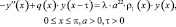(1)

с начальным условием

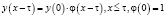, (2)

где t – запаздывание, 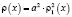– весовая функция, 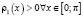, l – спектральный параметр, причём потенциал q(x) предполагается суммируемой функцией на отрезке :

.

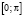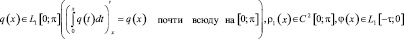Пусть 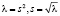– ветвь корня, для которой 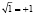. В работе получена асимптотика решения дифференциального уравнения (1)-(2) при 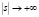(в зависимости от величины t).

Теорема.

Общее решение дифференциального уравнения (1) в случае 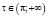имеет следующий вид:

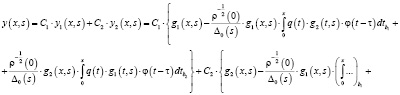
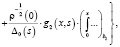где C1 и C2 – произвольные постоянные, 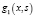и 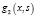– фундаментальная система решений вспомогательного уравнения

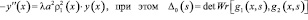– определитель Вронского решени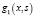й и 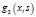.