Рассмотрим дифференциальное уравнение четвёртого порядка:
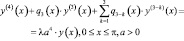(1)
с граничными условиями
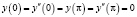, (2)
где l – спектральный параметр, коэффициенты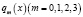 
– суммируемые функции на отрезке 
:
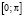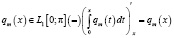почти всюду на отрезке 
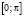. (3)
В случае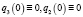 
асимптотика решений дифференциального уравнения (1) изучена в работе [1]. В случае 
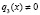в монографии М.А. Наймарка [2, глава 2, с. 53] указана замена 
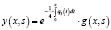, позволяющая преобразовать уравнение (1) к более простому виду:
.
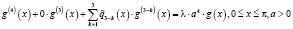Но это замена осуществима, только если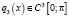 
, в случае 
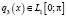она не проходит. В [1] доказана теорема.
Теорема.
Решение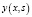 
дифференциального уравнения (1) имеет вид:
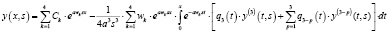, (4)
где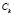 
– произвольные постоянные, 
.
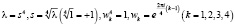Метод последовательных приближений (см. [1]) к интегральному уравнению (4) в случае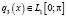 
также неприменим. Вопрос: как искать асимптотику решений уравнения (1)?