Рассмотрим следующую краевую задачу для дифференциального оператора восьмого порядка:
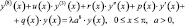 (1)
(1)
с граничными условиями вида
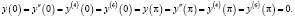 (2)
(2)
Предполагается, что все коэффициенты уравнения (1) являются суммируемыми на отрезке
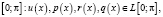 (3)
(3)
при этом напомним:
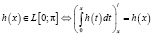
почти всюду на отрезке 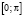 .
.
Для изучения граничных условий (2) необходимо изучить асимптотику решений дифференциального уравнения (1) при больших значениях спектрального параметра l. Будем следовать методике, разработанной автором в работах [1, 2, 3] для дифференциальных операторов второго и четвертого порядков.
Пусть 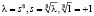 . Пусть
. Пусть 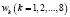 – различные корни восьмой степени из единицы:
– различные корни восьмой степени из единицы:
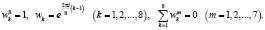 (4)
(4)
Теорема 1. Решение 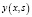 дифференциального уравнения (1) является решением следующего интегрального уравнения Вольтерры:
дифференциального уравнения (1) является решением следующего интегрального уравнения Вольтерры:
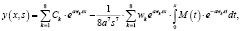 (5)
(5)
где
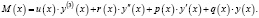 (6)
(6)
Доказать формулы (5) – (6) можно непосредственным дифференцированием этих формул с учётом гладкости коэффициентов (3) и свойством (4) и подстановкой получившихся выражений в дифференциальное уравнение (1).
Уточним асимптотические выражения (5) методом последовательных приближений Пикара: находим 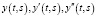 и
и 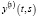 из формулы (5) и снова подставляем в (5), получая при этом, что справедливо следующее утверждение.
из формулы (5) и снова подставляем в (5), получая при этом, что справедливо следующее утверждение.
Теорема 2. Общее решение дифференциального уравнения (1) имеет следующий вид:
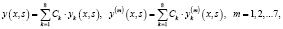 (7)
(7)
где
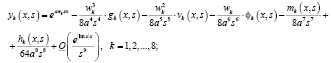 (8)
(8)
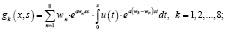 (9)
(9)
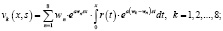 (10)
(10)
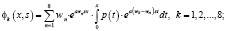 (11)
(11)
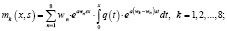 (12)
(12)
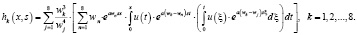 (13)
(13)
Аналогичные асимптотические формулы справедливы для функций
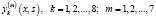 .
.
Формулы (7) – (13) позволяют изучить асимптотику собственных значений краевой задачи (1) – (2), как это было сделано ранее в работах [1, 2, 3].

