Рассмотрим дифференциальный оператор, заданный дифференциальным уравнением четвёртого порядка:
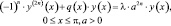(1)
где l – спектральный параметр, с граничными условиями
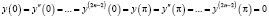, (2)
причём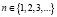 
, а потенциал 
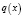является действительнозначной и суммируемой функцией на отрезке 
:
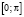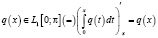почти всюду на отрезке [a,b]. (3)
В случае n=1 дифференциальный оператор (1)-(2) с условием (3) изучен в работе [1], в случае n=2 – в работе [2].
Теорема (основная). Асимптотика собственных значений дифференциального оператора (1)-(2) с условием (3) при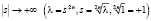 
имеет следующий вид:
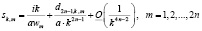, (4)
, 
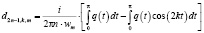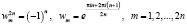. (5)