Из теории динамических систем [1-4] известен такой факт, что для достаточно общих семейств хаотических динамических систем существуют периодические возмущения, приводящие к стабилизации цикла заданного периода. Предлагаемый криптографический метод базируется на этом факте. Информация шифруется с помощью такого метода. В качестве передаваемого сигнала используются возмущения, а ключом для расшифровки полученного сообщения служит вид отображения (т.е. вид функции, задающей отображение).
Цель. Разработать криптографический метод на основе стабилизации хаотического поведения динамической системы. Провести исследования данного криптографического метода по всем необходимым параметрам.
Описание. Рассмотрим основные положения и результаты, полученные в теории динамических систем относительно стабилизации хаотического поведения. В настоящее время наиболее успешными методами стабилизации поведения (т.е. управления поведением) динамических систем являются метод мультипликативного воздействия с обратной связью и метод без обратной связи [4, 5]. Предположим, что рассматриваемая система задается обыкновенными дифференциальными уравнениями следующего вида:
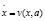, (1.1)
где х = {x1, ..., xn} – совокупность динамических переменных, v = {v1, ..., vn} – некоторая n-компонентная нелинейная функция и а – управляющий параметр. Проблема управления поведением системы (1.1) заключается в том, чтобы найти такое внешнее возмущение G, при котором фазовый поток Ft(x,G), порождаемый возмущенной динамической системой
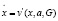(1.2)
стремился бы к выбранному подмножеству A(G) ее фазового пространства.
Подмножество A(G) может быть как аттрактором, так и неустойчивым множеством. В последнем случае возмущения G модифицируют систему (1.1) таким образом, что фазовые траектории подходят к подмножеству A(G) и остаются в достаточно малой его окрестностиU⊃A(G) под действием G .
Если внешние возмущения реализуются посредством мультипликативного воздействия по отношению к динамическим переменным хi, то говорят, что имеет место параметрическое (или мультипликативное) управление, поскольку, как правило, параметры мультипликативно включаются в динамическую систему.
В этом случае регулирование состоит в такой модификации функции v в соотношении (1.1), чтобы новая система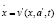 
имела бы требуемое (заранее выбранное) поведение. Здесь 
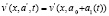и параметр a1(t) обычно является Т-периодической функцией.
Для параметрических возмущений с обратной связью учитывается текущее состояние системы: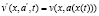 
. В этом случае параметр должен изменяться специальным путем, и необязательно периодически.
Достаточно часто в приложениях встречается ситуация, когда мультипликативное введение внешних возмущений в систему невозможно. Тогда фазовый поток Ft(x,G), раскладывается на две составляющие: часть, соответствующую невозмущенному фазовому потоку Ft(x), и компоненту Ft(G), которая инициируется исключительно возмущениями Ft(x,G) = Ft(x) + Ft(G). В этом случае имеет место аддитивное возмущение, т.е. v’(x,a’,t) = v(x,a) + g(t), где g(t) обозначает внешнее воздействие. Таким образом, управление динамикой системы подразумевает приложение силовой компоненты к векторной функции. Поэтому данный тип управления поведением динамической системы называется силовым. В свою очередь, если в силовом контроле учитывается обратная связь, то функция v модифицируется как v’i = vi (x,а) + gk(xi(t)), i = 1,2, ..., n, 1≤k≤n.
По ряду причин параметрический метод стабилизации динамики имеет определенные преимущества перед силовым. Во-первых, в приложениях к физическим, химическим и другим важным системам часто рассматриваются величины, которые являются пропорциональными динамическим переменным хi. Для таких систем v(0,a1,...,am) = 0, а гиперповерхности хi являются инвариантными множествами. Это означает, что система (1.1) отражает реальные процессы только на симплексе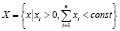 
.
В этом случае внешнее аддитивное воздействие может привести к тому, что фазовые траектории покинут множество X, пересекая гиперповерхности хj =0. Поэтому силовое воздействие может явиться причиной вырождения системы или выхода ее на нежелательный режим эволюции. Например, для биологических систем это означает вымирание части особей. В то же время, параметрическое воздействие означает изменение ресурсов системы и, таким образом, является более тонким в сравнении с силовым. Во-вторых, силовое возмущение гораздо труднее реализовать. Так, для химических систем силовой контроль подразумевает введение (и соответственно, удаление) дополнительных веществ; для биологических систем такой метод стабилизации может быть реализован через стерилизацию части особей или введением в сообщество дополнительных видов. С другой стороны, в противоположность параметрической стабилизации, силовой метод, как правило, приводит к требуемому результату для почти всех систем, поскольку во многих случаях ее естественное поведение может быть буквально «задавлено» внешней силой. Введение обратной связи является определенным преимуществом, поскольку в большинстве случаев такой способ управления приводит к требуемому результату: выбранный заранее седловой предельный цикл стабилизируется и, таким образом, исследуемая система выводится на требуемый режим движения. Однако этот метод эффективен, если только изображающая точка находится вблизи выбранного цикла. В противном случае необходимо использовать дополнительные способы воздействия. В то же время методы стабилизации без обратной связи не требуют введения постоянного компьютерного (или какого-либо другого) слежения за состоянием системы и менее подвержены воздействиям шумов, что существенно упрощает их использование в приложениях.
Основные результаты, полученные в теории динамических систем и относящиеся к стабилизации хаотического поведения внешними возмущениями без обратной связи, сводятся к следующему [5, 6]. Пусть задана динамическая система (отображение) Ta:M→M,
Ta:xf(x,a), (1.3)
где a∈A⊂ R и f = {f1, …, fn}, x = {x1, …, xn}. Допустим, что эта система при определенных значениях параметра может иметь хаотическое поведение, т.е. существует некоторое подмножество Аc, Ac⊂A , такое, что для a∈Ac динамика (1.3) (возможно, при некоторых начальных условиях) отлична от стационарной, периодической и квазипериодической. Для стабилизации хаотического поведения необходимо определить такое возмущение G, действующее на хаотическом множестве Аc, G :Аc→ Аc,
G:ag(a),a∈Ac, (1.4)
чтобы результирующая возмущенная динамическая система
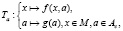(1.5)
обладала устойчивыми циклами. При периодическом возмущении преобразование G, задающее закон изменения параметра, определено лишь в конечном наборе точек {а1, a2, …, aτ} причем аi+1= g(ai), i=1,2,…t–1, и а1 = g(at), а1, a2, …, aτ∈Ac. В этом случае удобно каждому возмущению периода t параметра поставить в соответствие вектор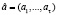 
из пространства 
.
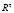Тогда можно рассмотреть множество
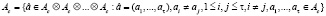
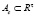, отвечающее всевозможным воздействиям периода t, оперирующим в Ac.
В работах [6, 7] было показано, что среди наборов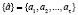 
, составляющих множество Аc, существуют такие 
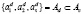, что отображение (1.5) обладает устойчивыми циклами конечных периодов, причем период t полученного устойчивого цикла всегда кратен периоду возмущения, t = τk, где k = 1,2,.... Такая ситуация оказывается типичной для большого класса хаотических отображений [8-10]. Более того, для любого семейства унимодальных и кусочно-линейных отображений возможно найти такие возмущения а1, a2, …, at, при которых соответствующие возмущенные семейства обладают устойчивыми циклами с предписанными периодами.
Этот результат основан на следующем свойстве: если для отображения Ta:xf(x,a), x∈M, а∈A, существует подмножество σ∈M такое, что для любых х1, х2∈s найдется a*∈A, для которого f(x1,a*) = x2 и имеется критическая точка хc∈σ такая, что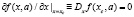 
при любом а∈A, то для любых x2, x3, ..., xt∈σ, t = τ, существуют такие х1 и а1, а2, ..., аt, что цикл (x1, x2, ..., xt) t = τ, будет устойчивым циклом возмущенного отображения Ta при параметрических возмущениях а1, a2, …, at.
В общем случае подмножество Ad, соответствующее стабилизированному поведению, имеет достаточно сложную структуру [9, 10]. Однако для квадратичного семейства
Ta:xax(1–x), (1.6)
с периодическим возмущением (а1, a2, …, at) подмножество Ad, отвечающее циклам периода t = τ оказывается целой областью и разбивается на такие подобласти, что возмущения из каждой такой подобласти приводят к стабилизации цикла определенного периода. Именно этот результат и позволяет эффективно использовать данное отображение для шифрования и пересылки скрытых сообщений.
Рассмотрим подробнее периодически (с периодом t) возмущенное семейство (1.6). Его удобно переписать в следующем виде:
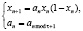(1.7)
Если это отображение имеет цикл периода t = τ, р = (x1, x2, ..., xt), то точки этого цикла будут удовлетворять следующей системе уравнений
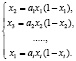(1.8)
Для решения обратной задачи, т.е. нахождения значений параметров, при которых отображение (1.7) имеет заданный цикл р = (x1, x2, ..., xt), необходимо выразить аi, из системы (1.8):
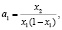
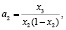
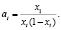(1.9)
Очевидно, что при этом не для всех хt∈ (0,1) имеет место ai∈ [0,4]. Однако при выполнении этого условия для любого цикла p = (x1, x2, ..., xt) найдутся такие параметры (а1, a2, …, at), при которых возмущенное отображение (1.7) будет обладать циклом р. При
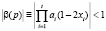
он будет устойчив.
С учетом равенств (1.9) это условие перепишется как:
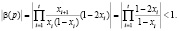(1.10)
Поскольку при хс = 1/2 имеем (l – 2хс)/(l– хс)= 0, то неравенство (1.10) всегда может быть выполнено. Множество значений (x1, x2, ..., xt), при которых ai∈ [0,4] и удовлетворяется неравенство (1.10), образует в пространстве Rt определенную область, каждая точка которой соответствует устойчивому циклу возмущенного отображения. Преобразуя эту область при помощи системы (1.9), получим соответствующую область значений параметров в параметрическом пространстве Rt.
Предлагаемый криптографический метод на основе стабилизации хаотического поведения динамических систем и будет использовать в качестве основополагающего начала для разработки алгоритмов криптографического преобразования информации на базе хаотического отображения.
Вывод. Предлагаемый криптографический метод базируется на таком известном факте из теории динамических систем: для достаточно общих семейств хаотических динамических систем существуют периодические возмущения, приводящие к стабилизации цикла заданного периода. Информация шифруется с помощью таких стабилизированных циклов. В качестве передаваемого сигнала используются возмущения, а ключом для расшифровки полученного сообщения служит вид отображения.
В настоящее время имеются программные средства, реализующие криптографический метод на основе стабилизации хаотического поведения динамических систем [11].