Субъективные оценки носят неопределенный характер и заключены в пределах некоторых интервалов, при этом оцениваемая величина может принимать любое значение из указанного интервала. Следовательно моделью субъективной оценки может служить случайная величина оценки, равномерно распределенная в границах интервала. Такую неопределенность будем называть интервально стохастической, а саму оценку – интервально стохастической (ИС).
Суждения субъекта основываются на ИС-оценках, поэтому его выводы и решения как в однокритериальных, так и многокритериальных проблемах, также будут носить неопределенный, причем интервальный характер. Окончательные, или глобальные критерии, характеризующие различные альтернативы, также будут носить интервальный стохастический характер, что затрудняет выбор наилучшей альтернативы, так как интервалы глобальных критериев могут пересекаться, образовывать общие области, внутри которых различные альтернативы становятся равнозначными. И для того чтобы субъект смог осуществить выбор компромиссной альтернативы в статье вводятся дополнительные критерии.
В существующей литературе для принятия решений в условиях неопределенности применяют два подхода. В первом походе неопределенность попросту игнорируется и принимается, что все оценки критериев, альтернатив и их сравнений между собой, служащие затем для принятия решения, являются однозначными (точечными). Таков, в частности, процесс аналитической иерархии (Analytic Hierarchy Process – AHP) [6]. При втором подходе [3, 8 – 10] с помощью разнообразных математических приемов неопределенность пытаются свести к полной определенности, сводя интервалы неопределенности к неким точечным оценкам, чтобы потом снова перейти к методам первого подхода.
В настоящей работе считается, что неопределенность при принятии решения, обусловленная интервальной неопределенностью субъективных оценок, является атрибутом реальной действительности. Поэтому для получения адекватных результатов необходимо рассматривать существующую неопределенность как объективную данность, а не помеху, от которой непременно следует избавиться. Такая концепция требует иных подходов и методов к анализу неопределенности и принятию решений при неопределенности.
В статье предлагается подход к многокритериальной оптимизации в условиях интервальной стохастической неопределенности субъективных оценок. В основу многокритериальной оптимизации положен процесс аналитической иерархии AHP, который изначально носит детерминированный характер и использует однозначные точечные оценки относительной важности критериев и альтернатив по критериям. Для поддержки принятия решения в условиях интервальной неопределенности вводится дополнительный критерий – интервальная устойчивость – характеризующий равнозначность различных альтернатив в общей области пересечения интервалов их глобальных приоритетов. Рассмотрен пример применения предлагаемого подхода к проблеме принятия решения при 4-х критериях и трех альтернативах. Проведено также сравнение результатов, получаемых по предлагаемому методу и с использованием методов интервального анализа [1], показавшее, что применение интервального анализа является некорректным и приводит к неоправданно широким интервалам неопределенности альтернатив.
Интервально-стохастический метод АНР
Метод АНР, как известно, используется для анализа решений в многокритериальных проблемах и основывается на построении матриц парных сравнений как для критериев, так и альтернатив относительно каждого критерия, с последующим определением собственных векторов, соответствующих максимальным собственным значениям этих матриц. Элементы собственных векторов соответствующих матриц парных сравнений представляют собой относительные коэффициенты важности критериев и альтернатив с точки зрения каждого критерия. Завершает процедуру АНР вычисление глобальных приоритетов (ГП) для каждой альтернативы и выбор наилучшей из них, соответствующей максимальному значению ГП.
Поскольку субъект не наделен способностью давать точные оценки, но только интервальные, то его субъективные оценки относительно степени превосходства одного фактора над другим, равно как и значений любых иных величин, носят принципиально размытый, неопределенный характер. В принципе, интервально стохастическая величина может иметь различные плотности вероятностей – треугольную, усеченную нормальную, усеченную логарифмически нормальную и пр. Однако, коль скоро оценивающий субъект не может давать точные оценки, тем более он лишен способности априори определить плотности вероятностей своих оценок [7].
В силу интервально стохастического характера субъективных оценок матрицы парных сравнений, их собственные значения и собственные векторы, в том числе коэффициенты относительной важности критериев и альтернатив, а также глобальные приоритеты (ГП) альтернатив, являются интервально стохастическими. Поэтому окончательное решение будет определяться уже не точечными детерминированными оценками ГП альтернатив, а их ИС-оценками.
Рассматриваемая математическая модель многокритериального принятия решений в условиях интервально стохастической неопределенности имеет вид {X, F,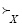 
, a(ω)} и включает:
– множество возможных решений, или альтернатив, X = (x1, x2, … , xn),
– векторный критерий F = (f1, f2, … , fm),
– отношение предпочтения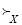 
, заданное на множестве возможных решений X,
– ИС-оценку величины / фактора a(ω), которая является интервальной величиной a(ω) 
[
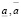] и, кроме того, величиной случайной и равномерно распределенной внутри интервала [
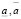] с плотностью вероятности p(a) = 1/Δ, 
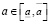, p(a) = 0, 
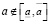, где 
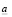и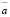 
– наименьшая и наибольшая границы интервала; 
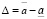– ширина интервала; ω 
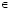Ω – элементарные события из пространства элементарных событий Ω.
Принятие решения в рассматриваемом здесь интервально стохастическом АНР проводится по следующему алгоритму:
1) задаются интервалы сравнительной важности критериев и альтернатив по каждому критерию и строятся соответствующие интервально стохастические матрицы (ИС-матрицы) парных сравнений,
2) для каждой ИС-матрицы парных сравнений определяются математические ожидания (МО), дисперсии (Д) и средние квадратические отклонения (СКО) случайных собственных векторов ИС-матриц, являющихся также векторами приоритетов критериев и альтернатив по каждому критерию,
3) по найденным значениям МО, Д и СКО векторов приоритетов вычисляются значения МО, Д и СКО для ГП каждой альтернативы,
4) определяются границы интервалов изменения ГП в виде МО ± ε∙СКО, где ε определяет ширину интервала ГП,
5) определяются общие области для различных альтернатив, которые являются пересечениями интервалов ГП альтернатив,
6) вычисляется дополнительный критерий, названный в статье интервальной устойчивостью,
7) в соответствии с расположением границ интервалов ГП и значениями критерия интервальной устойчивости принимается окончательное решение.
Далее приводятся методы определения величин, используемых для реализации алгоритма.
В интервально стохастическом АНР собственные векторы являются случайными и для их характеристики необходимо определять значения МО, Д и СКО.
Запишем ИС-матрицу парных сравнений в условиях рассматриваемой модели
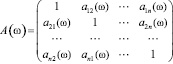, (1)
где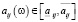 
– ИС оценка относительной значимости i-го фактора над j-м при их парном сравнении, осуществляемом по фундаментальной шкале [6]; 
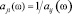(i, j = 1, 2,…, n) для каждой реализации ω 
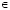Ω, при этом границы интервала изменения элемента 
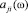равны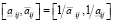 
.
В интервально стохастическом АНР для каждой реализации ω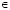 
Ω случайные элементы wi (ω) случайного собственного вектора W(ω) = (w1(ω), w2(ω), … , wn(ω)) у ИС-матрицы А(ω) вычисляются согласно следующему выражению:
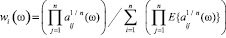, (2)
где E{∙} – оператор МО.
Учитывая, что в каждой i-й строке ИС-матрицы А(ω) случайные величины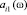 
, 
, …, 
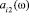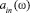являются независимыми получим согласно (2) выражения для вычисления МОwi = E{wi (ω)}, Дwi = E{
} ‒ 
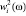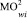и СКОwi = (Дwi )1/2 элементов wi (ω), i = 1, 2,…, n, собственного вектора W(ω) c
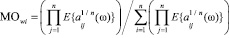, (3)
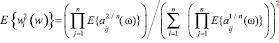. (4)
МО различных степеней случайных величин aij(w) в (3), (4) в силу равномерности распределения aij(w), будут равны:
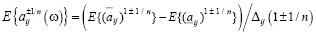, (5)
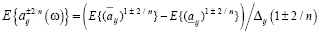. (6)
В рассматриваемом интервально стохастическом методе АНР матрицы парных сравнений являются ИС-матрицами, а их собственные векторы (приоритеты критериев) wF(ω)=(wf 1(ω)i, wf 2(ω), …, wf m(ω)) и собственные векторы (приоритеты альтернатив по каждому критерию)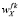 
(ω) = (
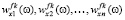) – случайными, поэтому для их характеристики необходимо знать МО, Д и СКО элементов случайных векторов приоритетов.
Значения ГП альтернатив в АНР, по величине которых производится окончательный выбор наилучшего решения в многокритериальной проблеме, вычисляются как сумма произведений приоритетов данной альтернативы на приоритеты каждого критерия. В интервально стохастическом АНР ГП альтернатив будут случайными Гxi(ω) и для альтернативы xi они определяются следующим выражением (i = 1, 2,…, n):
Гxi(ω) =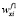 
(ω)∙wf 1(ω) + 
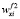(ω)∙wf 2(ω) + ... + 
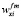(ω)∙ wf m(ω), (7)
где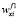 
(ω),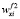 
(ω), … , 
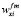(ω) – приоритеты альтернативы xi по критериям f1, f2, …, fm; wf 1i(ω); wf 2(ω), …, wf m(ω) – приоритеты критериев.
Поскольку случайные величины приоритетов альтернатив и критериев в (7) независимы между собой, то значения
МОГi = E{wГi (ω)}, ДГi = E{(wГi (ω) – E{wГi (ω)})2} и СКОГi = (ДГi )1/2
будут равны [5]:
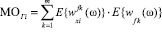, (8)
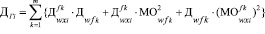. (9)
Границы интервалов, внутри которых с доверительной вероятностью Рε будут лежать случайные величины ГП составят
;
.
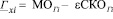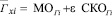Иначе говоря, значения Гxi для каждой альтернативы xi будут заключены в интервалах
МОГi – ε∙СКОГi ≤ Гxi (ω) ≤ МОГi+ + ε∙СКОГi.
Число ε целесообразно выбрать равным 3.
Полученные в интервально стохастическом АНР интервалы возможных значений ГП служат далее основанием для определения наилучшей альтернативы. Целесообразно выбирать такое интервальное решение, для которого его наименьшая и наибольшая границы ГП имеют максимальные значения среди границ всех остальных интервалов ГП. На рис. 1 таковым является интервал, соответствующий альтернативе x’, поскольку его наименьшая и наибольшая границы имеют максимальные значения. В соответствии с этим наихудшей будет такая альтернатива (x’’, рис. 1), для которого наименьшая и наибольшая границы интервала ГП являются минимальными.
Ввиду того, что наилучшее решение в интервально стохастическом методе АНР определяется на основании интервальных оценок, возникает аспект устойчивости интервальной альтернативы, который отсутствует при выборе точечной оценки альтернативы. Действительно, в ряде случаев интервалы ГП различных альтернатив могут пересекаться между собой, образуя общий интервал (ОИ) значений, внутри которого альтернативы, имеющие общие значения глобальных приоритетов, приводят к одинаковым последствиям. Поэтому в ОИ наилучшая альтернатива имеющая максимальные значения наименьшей и наибольшей границ интервала ГП будет не лучше другой альтернативы. Указанный аспект назовем интервальной устойчивостью данной альтернативы, которая определяется как
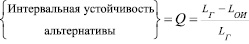. (10)
где LГ – длина интервала ГП; LОИ – длина интервала ОИ; 0 ≤ Q ≤ 1.
Если длина LГ = LОИ, то интервальная устойчивость Q = 0 и данная альтернатива будет ничем не лучше другой. Если LОИ = 0, то интервальная устойчивость будет максимальной и равной Q = 1. Наилучшая альтернатива будет соответствовать той из них, которая имеет максимальные значения наименьшей и наибольшей границ ГП.
Пример применения интервально стохастического АНР
Рассмотрим многокритериальную проблему выбора из трех альтернатив x1, x2, x3, оцениваемых с точки зрения четырех критериев f1, f2, f3, f4. ИС-матрицы парных сравнений имеют следующий вид:
– для критериев f1, f2, f3, f4
,
– для альтернатив x1, x2, x3 относительно каждого критерия f1, f2, f3, f4
,
,
,
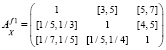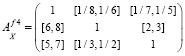
Приведение разнородных качественных и количественных критериев к единой однородной шкале рассмотрено в [2, 4].
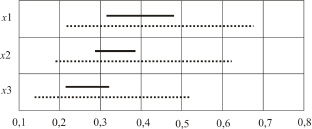
Границы интервалов ГП альтернатив, полученные по интервально стохастическому АНР (сплошные линии) и интервальной арифметики (пунктирные линии)
Вычисления значений МО, Д и СКО случайных собственных векторов ИС-матриц парного сравнения проводились согласно выражениям, полученным выше. На рисунке приведены границы интервалов ГП, вычисленные по методу интервально стохастического АНР (сплошные линии) и, для сравнения, по правилам интервальной арифметики (пунктирные линии). Полученные интервалы возможных значений ГП, а также значения интервальной устойчивости, служат основанием для выбора наилучшей альтернативы. В рассматриваемом примере таковым является интервал, соответствующий альтернативе x1 (рис. 1). Интервалы значений ГП двух интервальных альтернатив x1 и x2, одна из которых (x1) является претендентом на наилучшую, пересекаются по множеству ОИ, равному интервалу [0,315, 0,378]. Так как LОИ = 0,063, LГ x1 = 0,157 для альтернативы x1, поэтому интервальная устойчивость альтернативы x1 согласно (10) составит
Qx1 = (LГ x1 – LОИ) / LГ x1 = = (0,157 – 0,063) / 0,157 = 0,6,
то есть 60 %-ю интервальную устойчивость. Интервальная устойчивость альтернативы x2, интервал которой пересекается с интервалом альтернативы x1, составляет величину
Qx2 = (LГ x2 – LОИ) / LГ x2 = = (0,088 – 0,063) / 0,0,088 = 0,3,
то есть 30 %-ю интервальную устойчивость, которая в два раза меньше таковой (60 %) для альтернативы x1.
Было проведено также сравнение интервалов значений ГП (рис. 1), вычисленных, с одной стороны, по предложенному интервально стохастическому АРН, а с другой – с использованием операций интервальной арифметики. Оно показало, что длина последних в несколько раз превышает длину первых, что неоправданно и вызывается только правилами интервальной арифметики, но не содержательным смыслом неопределенности. Применение интервальной арифметики для принятия решений в многокритериальных проблемах по интервально стохастическому АНР некорректно, поскольку конечный выбор всегда будет зависеть от порядка применения операций интервальной арифметики и вида преобразованного выражения.
Заключение
Разработанный в статье интервально стохастический АНР расширяет детерминированный АНР на условия интервально стохастической неопределенности. Полученные выражения позволяют определять значения МО, Д и СКО случайных собственных векторов ИС-матриц парного сравнения и ГП альтернатив, по которым затем определяются интервалы ГП. Наилучшая интервальная альтернатива выбирается исходя из двух критериев: (1) по максимальным значениям наименьшей и наибольшей границ интервалов ГП, (2) по максимуму интервальной устойчивости альтернативы. Введение этого понятия оправдывается тем, что для выбора наилучшей альтернативы недостаточно знания только расположения границ интервала ее ГП, необходимо также знать область, при переходе к которой одна альтернатива изменяется на другую или становится не лучше конкурирующей альтернативы. Сравнение интервалов ГП альтернатив, полученных по предлагаемому интервально стохастическому АНР и с помощью интервальной арифметики, показывает их существенное отличие друг от друга. Предлагаемый подход приводит к значительно более узким интервалам неопределенности для ГП альтернатив, чем подход, основанный на операциях интервальной арифметики, которые дают результаты неадекватные реальности.
Интервально стохастический метод АНР, предлагаемый в данной статье, предназначен для принятия решений в условиях многокритериальности и интервально стохастической неопределенности оценок, что отражает реальные условия выбора и психологию принятия решений.