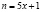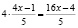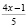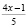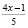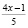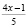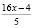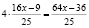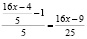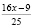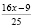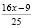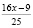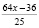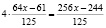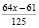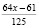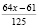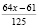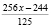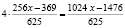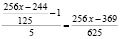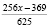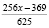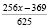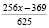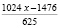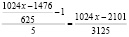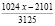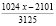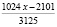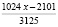Scientific journal

International Journal of Applied and fundamental research

ISSN 1996-3955

ИФ РИНЦ = 0,593

Несмотря на то, что математика является самым многочасовым предметом из всех предметов изучаюшихся в школе всего мира, интерес к этому предмету становится все меньше. Дети осознанно выбирают предметы связанные с природой и повседневной жизнью для будущей профессии. Наше исследование направлено для детей, у которых есть способности, но нет интереса к математике. Методы преподавания математики предложенные нами и названная «занимательные» акцентирует особое внимание на интересных фактах, способных привлечь внимание обучающихся математике. Занимательные методы преподавания математики, как и занимательная математика служат «поставщиком новых идей и задач» [1]. Занимательные методы преподавания предлогают применять в процессе обучения математики: занимательную математику, исторических сведении, компьютерных анимации, японских Оригами и др. материалов для доступного и интересного изложения: математических предложении, задач, формул в процессе преподавания математики, а также углубляют понимание, развивают логическое и критическое мышление, повышают наблюдательность учащихся и интерес к изучению математики.

Занимательные методы преподавания математики применяются при профессиональной подготовке будуших учителей математики в педагогических вузах, преподавании математики в средних школах и при подготовке детей к школе. При этом используются в учебном процессе занимательные материалы, активизирующие логическое и критическое мышление обучающихся и формирующие способности к изучению математики.

Целью исследования является построение методической системы обучения и учебно-методического комплекса элективного курса математики для развития логического и критического мышления учащихся посредством применения «занимательных методов преподавания математики» на основе психолого-педагогических, дидактических, методико-математических теорий и концепций, а также разработка конкретных практических рекомендаций и поднотовка методического пособия.

Объектом данного исследования является математическая подготовка будущего учителя. Предмет исследования – методическая система обучения элективному курсу математики в педагогическом вузе. Уровень профессиональной подготовки по преподаванию математики в средней школе будет более эффективным, если:

– опираться на психолого-педагогические исследования по проблемам профессионализации личности и профессионализации обучения,

– учитывать особенности элективного курса «Занимательные методы преподавания математики» как учебного предмета,

– определить критерий профессиональной подготовки будущих учителей по развитию логического и критического мышления учащихся посредством «занимательных методов преподавания»,

– на основе анализа историко-математической, научно-методической и учебной литературы по «занимательным методам преподавания математики», школьных учебников и учебных пособии для вузов разработать методы, реализующие взаимосвязь со школьным предметом математики и элективным курсом «Занимательные методы преподавания математики» в педвузе,

– опираясь на анализ психолого-педагогического исследования и методов взаимосвязи, выявить основные характеристики профессионально-педагогической подготовки учителей математики, посредством занимательных методов обучения,

– выявить условия построения и функционирования учебно-методического комплекса элективного курса «занимательные методы преподавания математики» для будущих учителей математики;

– разработать на основе выявленных возможностей конкретные практические рекомендаций и методическое пособие для студентов по совершенствованию математической подготовки будущего учителя.

Опираясь на базовые программы и принципы обучения школьного курса математики и педагогического вуза, нами разработана методическая система обучения элективному курсу математики в педагогическом вузе, создан учебно-методический комплекс курса по занимательной математике; исследована специфика отдельных компонентов методической системы для обучения, разработано методическое пособие [2] и сборник тестов по занимательной математике [3], учебник по методам преподавания математики [4], разработаны методы преподавания математики с помощью компьютерной анимации; рассмотрены вопросы развития профессиональной подготовки будуших учителей математики в области применения занимательной математики; предложена методика применения занимательной математики для развития способностей логического и критического мышления учащихсяя, не успевающих по математике; предложен учебно-методический комплекс преподавания элективного курса профессиональной подготовки будущих учителей математики в современной школе, а также с точки зрения педагогических требований определена эффективность применения «занимательной методики преподавания математики» как средства развития способностей логического мышления учащихся на уроках математики.

Применение в процессе обучения: исторических сведении, занимательных задач, литературных книг, энциклопедических материалов и др. на ряду с учебниками по математике не только развивают логическое и критическое мышление обучающихся, но и создают условие для понимание математических предложении, учат находить правильное решение, связывает математику с природой и с повседневной жизнью.

Один из методов занинересовать учащихся решению задач является применение исторических сведений и литературных сюжетов в процессе урока.

Пример. 9-го ноября 1926 года американской газете «Сатердей ивнинг пост» был опубликован небольшой расказ Б.Э. Ульямса под названием «Кокосовые орехи». Известный американский математик Мартин Гарднер в свое время решил эту задачу, применяя отрицательные числа и назвал свой метод «Метод отрицательных орехов».

В книге Гарднер не дает развернутое решение головоломки этим методом. Простому школьнику не по силам понять объяснение решение задачи приведенного в книге. Поэтому мы приводим занимательный метод решение задачи. Мы даем развернутое решение старого варианта этой задачи в табличной форме, так как краткое решение очень трудно для понимание учащимся средней школы.

Текст задачи-головоломки «Мартышка и кокосовые орехи» из книги Мартина Гарднера «Математические головоломки и развлечения» [5]: пять матросов и мартышка потерпели кораблекрушение и высадились на необитаемом острове. Весь день они занимались сбором кокосовых орехов. Вечером они сложили все орехи в кучу и легли спать.

Ночью, когда все заснули, один из матросов, подумав, что утром при разделе может вспыхнуть ссора, встал, чтобы взять свою долю орехов немедля. Он разделил все кокосовые орехи на пять равных кучек, а один оставшийся орех отдал мартышке. Затем матрос спрятал свою долю, а все остальные орехи снова сложил в одну кучу. Через некоторое время проснулся другой «рабинзон» и сделал то же самое. У него тоже остался один лишний орех, и он отдал его мартышке. И так один за другим поступили все пятеро потерпевших кораблекрушение. Каждый из них взял себе одну пятую орехов из той кучи, которую он нашел при пробуждении, и каждый отдал один орех мартышке.

Утром они поделили оставшиеся орехи, и каждому досталось – по одной пятой (в старом варианте задачи один орех снова оказывается лишним и достается мартышке). Разумеется, каждый матрос не мог не знать, что часть орехов не хватает, но так как у каждого из них совесть была одинакова нечиста, то никто ничего не сказал. Сколько орехов было первоначально?

Дополнительно, нам нужно определить общее количество орехов; количество орехов, который получил каждый матрос и количество орехов, которое досталось мартышке.

Обозначим общее количество орехов через n, украденных первым матросом через x и доставшихся после утреннего равного деления каждому матросу через у.

Рассмотрим количество оставшиеся орехов, после каждого случая (табл. 1-6).

Таблица 1

Деление орехов первым матросом

Таблица 2

Деление орехов вторым матросом

Таблица 3

Деление орехов третьим матросом

Таблица 4

Деление орехов четвертым матросом

Таблица 5

Деление орехов пятым матросом

Таблица 6

Деление поровну оставщихся орехов утром

Итак,

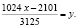
Отсюда: 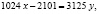если заменить 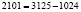, то

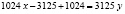
или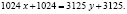

Вынесем общие множители за скобки: 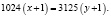Если учесть, что 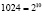, , 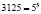то увидим, что 1024 и 3124 – взаимно простые числа. Тогда, для взаймно простых чисел 1024 и 3125 выполняется 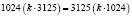(например. для взаймно простых чисел 5 и 7 выполняется: 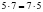или ).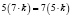

Зная,

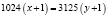и 

,

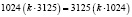имеем:

то есть

,

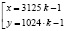(здесь 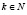). Если общее количество орехов (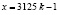) поставит на обозначенное: в начале решение задачи общее количество орехов 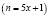, то получится:

,

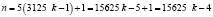то есть 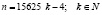и .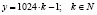

Итак, минимум возможное общее количество орехов при k=1 равно 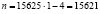(орехов), а у будет равно .

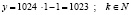Количество орехов украденных первым матросом: 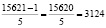(орехов). Оставшиеся количество орехов: 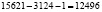(орехов). Если вычислить другим методом (по табл. 1), тоже: 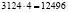(орехов) Количество орехов украденных вторым матросом: 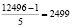(орехов). Оставшееся количество после этого: 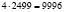(орехов). Количество орехов украденных третьим матросом: 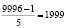(орехов). Оставшееся количество орехов после этого 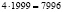(орехов). Количество орехов, украденных четвертым матросом: 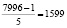(орехов). Оставшееся количество орехов после этого: 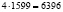(орехов). Количество орехов, украденных пятым матросом: 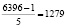(орехов). Оставшееся количество орехов после этого: 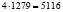(орехов).

Количество орехов, получивших при утреннем делении поровну каждым матросом: 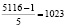(орехов), т.е. 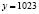(орехов).

Теперь мы можем определить общее количество орехов украденных и «честно» разделенных матросами (при 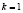). Всего первый матрос получил: 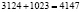(орехов); второй матрос получил всего: 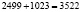(орехов); третьи матрос получил всего: 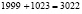(орехов); четвертый матрос получил всего: 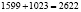(орехов) и пятый матрос получил всего: 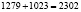(орехов). А мартышка получила всего 6 орехов.

Ответ: минимум возможное (при 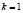) общее количество орехов равно: 15621. Соответствуюшее количество орехов полученные каждым маторосом: 4147, 3522, 3022, 2622, 2302. Мартышке дали 6 орехов.

Применение исторических и классических задач на уроке математики является одним из предлагаемых нами занимательных методов преподавания математики как занимательной, интересной и доступной науки.

Занимательные методы преподавания математики – это методы, позволяющие увеличить эффективность урока.