Согласно нормативным документам в регионах распространения многолетнемерзлых грунтов при подземной прокладке тепловых сетей, строящихся по принципу сохранения мерзлоты (принцип I), бесканальная прокладка не допускается [1]. Поэтому строительство подземных тепловых сетей возможно по принципу II (без сохранения многолетнемерзлых грунтов). Тем не менее, при строительстве подземных теплопроводов стремятся максимально уменьшить их влияние на мерзлый грунт путем уменьшения заглубления теплопровода с одновременным увеличением толщины теплоизоляции. В то же время, при чрезмерном уменьшении заглубления и увеличении толщины теплоизоляции теплопровода температура поверхности оболочки может достигать значений ниже допустимой температурной границы эксплуатации полиэтилена (минус 15 °С). При температурах ниже допустимой температуры эксплуатации, полиэтилен, из которого изготовлена оболочка, становится хрупким, что может привести к трещинам в материале при пучениях грунта. При попадании по трещинам влаги теплоизоляционный материал существенно теряет свои свойства. Кроме того, повторное многократное замерзание воды в микротрещинах полимерных материалов теплопровода неизбежно приводит к его преждевременному выходу из строя.
Целью данной работы является исследование изменения температуры поверхности оболочки во времени на основе математического моделирования теплового процесса при эксплуатации подземного трубопровода теплоснабжения в регионах распространения многолетнемерзлых грунтов.
Постановка задачи. В большинстве работ по исследованию влияния подземного полимерного трубопровода теплоснабжения в процессе эксплуатации на многолетнемерзлый грунт температурная задача решается методом конечных разностей в декартовой системе координат. При таком подходе возникают сложности с аппроксимацией границ рассматриваемой области. В плоском случае границы расчетной области представляют собой отрезки прямых и полуокружностей, что затрудняет выбор системы координат для построения расчетной сетки. При использовании декартовой системы координат приходится аппроксимировать окружности ломаными линиями, что, естественно, влияет на точность определения температурного поля в многослойной трубе ввиду наличия условий теплового контакта между трубой и теплоизоляцией. При исследовании влияния теплоносителя в трубе на тепловое состояние грунта, приближенное задание границ в непосредственной близости от теплообменной поверхности может привести к существенным погрешностям при определении границ оттаивания. Для более точного описания температурного поля в окрестности трубы с теплоносителем перспективным представляется решать задачу в полярных координатах. Естественно, при этом будут приближенно описаны прямые участки границ области, что также снизит точность расчета, но можно предположить, что их влияние на определение границ оттаивания грунта будет значительно ниже.
Примем допущение, что температурный режим теплоносителя в трубопроводе вдоль осевой координаты меняется слабо, а величина заглубления теплопровода практически не меняется по трассе, что позволяет пренебречь тепловыми потоками вдоль теплопровода. Используем фронтовую модель процесса промерзания-оттаивания грунта в виде классической задачи Стефана, учитывающую теплоту фазового перехода на границе мерзлого и талого грунта. Тогда тепловой процесс в системе «труба-грунт» описывается двумерным уравнением теплопроводности в полярных координатах (рис. 1).
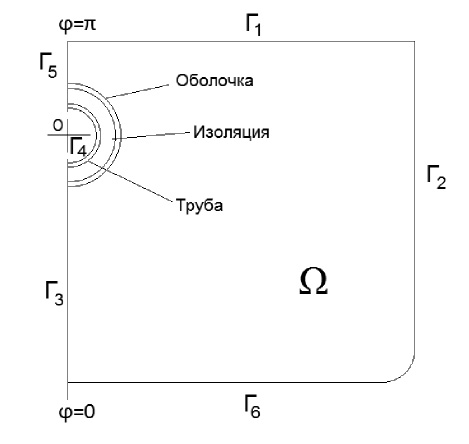
Рис. 1. Расчетная схема системы «многослойная труба-грунт»
Математическая постановка задачи Стефана со сглаженными коэффициентами формулируется следующим образом. Требуется определить нестационарное температурное поле 
, удовлетворяющее уравнению теплопроводности в полярных координатах:
(1)
граничному условию на дневной поверхности грунта:
; (2)
граничным условиям на границах Г2, Г3 и Г5:
, (3)
; (4)
граничному условию на внутренней поверхности теплопровода:
, (5)
(6)
и начальному условию:
. (7)
На границах слоев заданы условия идеального теплового контакта:
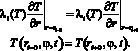i=1,2,3. (8)
Здесь T – температура; Tн – начальное распределение температуры; Tмг – температура многолетнемерзлого грунта; сρ(T), l(T) эффективные (сглаженные) коэффициенты объемной теплоемкости и теплопроводности, учитывающие теплоту фазового перехода и влажность грунта [2, 3]; a – коэффициент теплообмена свободных поверхностей; r, j –полярные координаты; t – время.
Нестационарное температурное поле в грунте с теплоизолированной трубой определялось решением системы (1)–(8) методом конечных разностей [4]. Используемый алгоритм решения задачи приведен в работе [5].
Результаты расчетов. В водяных подземных тепловых сетях, как правило, подающий и обратный трубопровод прокладываются совместно в одном ряду, в котором также располагают трубопроводы для горячего и холодного водоснабжения. В этом случае при расчетах пучок труб можно рассматривать как одну трубу с эквивалентным радиусом [6]. При расчетах рассматривался трубопровод с эквивалентным радиусом 81,5 мм. Значения теплофизических характеристик материалов, принятые в расчетах, приведены в таблице.
Теплофизические характеристики грунта и материалов теплопровода
|
Параметр |
Труба из сшитого полиэтиленa |
Изоляция из пенополиуретана |
Оболочка из полиэтилена |
Талый грунт |
Мерзлый грунт |
|
Коэффициент теплопроводности, Вт/(м·К) |
0,35 |
0,05 |
0,42 |
1,4 |
1,5 |
|
Плотность, кг/м3 |
938 |
33 |
960 |
1700 |
1700 |
|
Удельная теплоемкость, Дж/(кг·К) |
2300 |
1800 |
1700 |
1850 |
1750 |
Температура теплоносителя вне отопительного периода Tводы =10 °С, в отопительный период, Тводы от 80 до 95 °С в зависимости от температуры наружного воздуха; коэффициент теплообмена на внутренней поверхности трубы в отопительный период a=20 Вт/(м2· °С), вне отопительного сезона a=10 Вт/(м2· °С); коэффициент теплообмена на дневной поверхности летом a= 8,7 Вт/(м2· °С), зимой – a= 4 Вт/(м2· °С); влажность грунта 17, 65 %, температура и теплота фазового перехода 0 °С и 333,3 кДж/кг соответственно; 
.
Расчет начинался с апреля месяца. За начальное распределение температуры в грунте принимается однородное распределение со значением –3 °С. Полученное распределение температуры в системе «труба-грунт» в начале третьего отопительного сезона берется за начальное распределение температуры, полагая, что за этот период влияние заданного приближенного начального условия становится минимальным. Согласно нормативным документам среднесуточная температура окружающего воздуха для начала отопительного сезона не превышает 8 °С. Изменение температуры окружающего воздуха во времени описывалось функцией среднесуточных температур:
. (9)
Заглубление тепловых сетей до верха оболочки при бесканальной прокладке принимается не менее 0,7 м [1].
Исследовалось изменение во времени температуры на верхней (j=180°) и нижней (j=0°) точках внешней поверхности оболочки при заглублении верха теплопровода на 70 см (рис. 2).
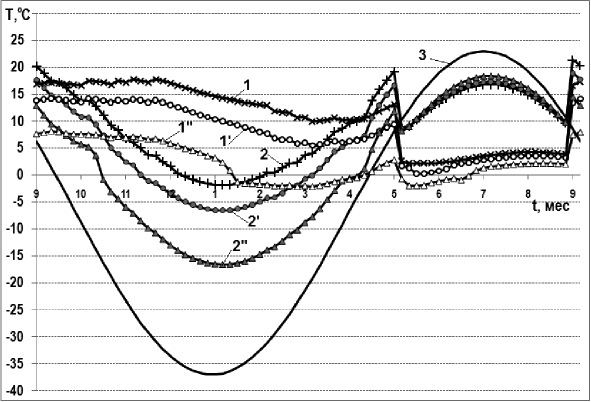
Рис. 2. Изменение температуры на внешней поверхности кожуха подземного теплопровода при заглублении 70 см и толщинах теплоизоляции d=3 см (кривые 1, 2), d=4 см (кривые 1′, 2′): 1, 1′ – при j=0° (нижняя точка); 2, 2′ при j=180° верхняя точка); 3 – среднесуточная температура окружающего воздуха
Расчеты показывают, что при таком заглублении температуры в верхней и нижней частях внешней поверхности теплопровода существенно отличаются. Температура верхней части поверхности кожуха под воздействием температуры окружающего воздуха достигает минимального значения около –17 °С в самый холодный период при толщине теплоизоляции 5 см, –8 °С – при толщине 4 см и –2 °С – при толщине 3 см. Согласно расчетным данным при заглублении теплопровода на 70 см толщина слоя теплоизоляции 5 см недопустима.
Вне отопительный период температура верхней части поверхности оболочки теплопровода на 5-12 °С выше температуры нижней части, что объясняется влиянием снизу многолетнемерзлого грунта. На верхней части превалирует влияние температуры окружающей среды.
Для теплоизолированных двухтрубных трубопроводов водяных сетей при подземной бесканальной прокладке существуют нормы линейной плотности теплового потока в Европейском регионе России, согласно которым определяется толщина теплоизоляции [7]. В других регионах следует применять коэффициент К, учитывающий изменение стоимости теплоты в зависимости от района строительства. Определенная таким образом толщина теплоизоляции может не удовлетворять по допустимой температурной границе эксплуатации материала оболочки.
При увеличении заглубления с 70 до 110 см закономерности изменения температуры внешней поверхности оболочки по времени сохраняются. Значения температуры повышаются незначительно – на 3-4 °С (рис. 3). При заглублении теплопровода на 110 см слой теплоизоляции толщиной 5 см обеспечивает удовлетворение лимитирующему условию по температуре.
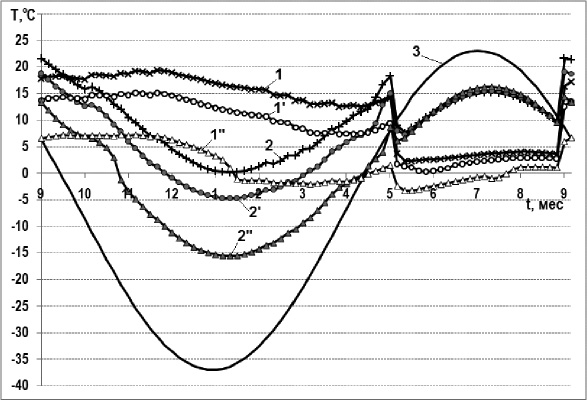
Рис. 3. Изменение температуры на внешней поверхности кожуха подземного теплопровода при заглублении 110 см и толщинах теплоизоляции d=3 см (кривые 1, 2), d=4 см (кривые 1′, 2′): 1, 1′ – при j=0° (нижняя точка); 2, 2′ при j=180° (верхняя точка)
Выводы
Предложенная математическая модель теплового процесса в системе «многослойная труба-грунт» в виде уравнения теплопроводности в полярных координатах эффективна для анализа динамики температуры поверхности оболочки бесканального подземного теплопровода в многолетнемерзлом грунте;
Расчетами показано, что для определения толщины слоя теплоизоляции и величины заглубления подземного теплопровода, эксплуатируемого в регионах распространения многолетнемерзлых грунтов, необходимо учитывать лимитирующее условие по температуре для материала оболочки.