Налоговый ресурс для развития региона всегда являлся значимым стратегическим ресурсом. Важной особенностью региональной налоговой политики является получение максимального налогового дохода при обязательном условии баланса экономической и социальной составляющих налоговой политики в целом. При этом актуальной является не только задача разработки экономико-математического аппарата в виде оптимизационных математических моделей, но и создание систем поддержки принятия решений в форме пакетов прикладных программ, обрабатывающих соответствующую модельную и статистическую информацию. В данной работе приводятся полученные с помощью автоматизированной программной системы [1] результаты численного анализа частного случая многокритериальной модели [3], в которой рассматриваются технико-экономические и бухгалтерские особенности функционирования предприятий регионального производственного сектора с учетом налогового окружения, а также интересов населения региона в соответствии с концепцией, подробно описанной в работе [2]. Содержательная постановка задачи имеет следующий вид. Рассматривается инвестиционный проект (ИП) по производству пользующейся спросом в регионе продукции n видов. При этом известны технико-экономические характеристики основных производственных фондов (ОПФ) n производящих отраслей – средние значения суммарной стоимости, сроков службы оборудования, производительности единицы ОПФ и стоимость единицы производимой продукции каждого вида. Требуется определить суммы инвестиций в производство, при которых суммарный дисконтированный денежный поток налоговых поступлений в регион, порождаемый данным ИП за определенный период, будет максимальным. Считается, что выполнены следующие предпосылки: 1) при расчете чистой прибыли производственного сектора региона учитываются налоги, составляющие наибольшую часть затрат предприятий, производящих соответствующую продукцию, 2) задана или определяется экспертными методами средняя доля β отчислений объемов выручки от реализации в фонд оплаты труда; 3) предприятия одной отрасли выпускают однородную (в смысле стоимости, спроса) продукцию на однородных (в смысле стоимости, производительности, срока службы) ОПФ, 4) объем выпуска продукции не превышает либо спрос на нее, либо фондоотдачу ОПФ.
Управление налоговой политикой на уровне региона должно осуществляться на основе оптимизационных математических моделей, позволяющих оценивать налоговый потенциал. Здесь рассматривается разновидность модели, предложенной в работе [2], когда не учитываются дотации регионального центра производителю и потребителю, спрос на продукцию отраслей фиксирован, а действие ИП ограничивается одним периодом (горизонтом планирования), что позволяет представить ИП в виде задачи линейного программирования:
;
;
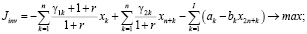
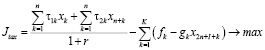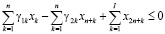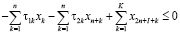; (1)
;
;
;
;
;
;
,
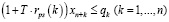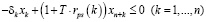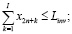
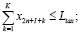
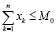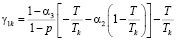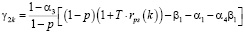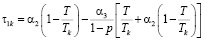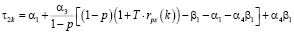где n – количество ОПФ; I, K – соответственно количество рисков для производственного сектора и управляющего центра; xk – стоимость приобретаемых ОПФ k-го вида (инвестиции в основные фонды); xn+k – выручка от продажи продукции, произведенной на k-м ОПФ; x2n+i (i=1,…,I) – затраты на избежание (устранение) i–го риска производственного сектора; x2n+I+k (j=1,…,K) – затраты на избежание (устранение) k–го риска потребительского сектора; сk – стоимость k-го ОПФ; Pk – стоимость продукции, произведенной на k-ом ОПФ; Vk – производительность k-го ОПФ; Tk – время полезного использования k-го ОПФ; T – горизонт планирования инвестиционного проекта; r – ставка дисконтирования на всем горизонте планирования; qk – спрос на продукцию, произведенную на k-м ОПФ;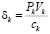 
– максимальная фондоотдача k-го ОПФ производственной подсистемы;ak, fk – максимальные издержки в случае отсутствия затрат на k-ом рисковом направлении функционирования производственной и управляющей подсистем соответственно; bk, gk – весовые коэффициенты относительной значимости k-го направления функционирования производственной и управляющей подсистем соответственно; rps(k) – экспертно задаваемые коэффициенты, отражающие, во сколько раз выручка на стадии послепродажного сервиса больше выручки от продаж k-го вида продукции; αi, i=1,…,4 – соответственно ставки налогов на добавленную стоимость, на имущество и на прибыль, а также страховых взносов производственного сектора региона; p – средний процент оборотных затрат в регионе в сумме всех затрат регионального производственного сектора; β – средний процент выручки от продаж регионального производственного сектора, выделяемый на ФОТ; Linv, Ltax – соответственно максимальные затраты на избежание (устранение) всех выделенных рисков производственного сектора и управляющего центра.
Модель (1) является частным (двухкритериальным) случаем модели, описанной в работе [4], но и одновременно обобщающую ее на случай α1≠0. Многопараметрическая, многокритериальная задача линейного программирования (1) решается и анализируется с помощью пакета программ [1]. Указанный пакет может использоваться в двух режимах. Пользователь-математик может в визуальном режиме (в смысле наглядного представления матричной информации) создавать и корректировать математические модели в форме многокритериальных задач линейного программирования. Экономист-аналитик с помощью [1] может самостоятельно формировать конфигурацию ИП (структуру и тип информации), заносить входную статистическую информацию, визуализировать решение в виде таблиц и графиков многопараметрических зависимостей, построения Парето-множеств и т.п.
На рисунке приведены полученные с помощью [1] зависимости значений чистой приведенной стоимости некоторого модельного ИП от параметра μ, отвечающего в нем за перераспределение интересов (максимизацию собственных средств) от налогового органа (μ≈0) к интересам производителя (μ≈1) при варьировании такого параметра, как, например, ставка налога на прибыль при α3=0.2 (график 1); α3=0.3 (график 2); α3=0.4 (график 3); α3=0.45 (график 4); α3=0.5 (график 5). График 1 на рисунке свидетельствует о наличии значимой зависимости (от NPV≈10 при μ≈0 до NPV≈35 при μ≈1) эффективности ИП от того, в чьих интересах она рассматривается. Вместе с тем, анализ рисунка позволяет сделать вывод о наличии оптимальной ставки α3≈0.45 (график 4), при которой практически отсутствует зависимость эффективности ИП от интересов его участников. Это может дать возможность управляющим органам региона определять, например, социально-экономическую эффективность проекта в регионе, если она является соответствующей целью анализа ИП.
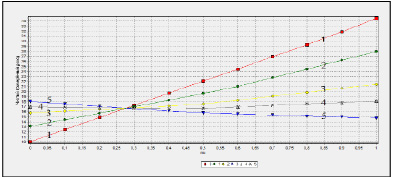
Зависимости NPV(μ) при варьировании ставки налога на прибыль
Пакет программ [1] дает удобную возможность экономисту-аналитику получать обширную и разнообразную графоаналитическую информацию по вопросам налогообложения в регионе: 1) объемы инвестиций, необходимые для максимизации налоговых поступлений в регион с учетом интересов нескольких заинтересованных сторон; 2) диапазоны чувствительности ИП к инвестициям по параметрам стоимости активов, стоимости произведенной на них продукции, спроса и отчислений в фонд оплаты труда, налоговых ставок; 3) зависимости налоговых поступлений от различных параметров модели и т.п.
Полученные результаты позволяют региональному центру принимать обоснованные решения по управлению региональной налоговой политикой, исходя из принципиальной возможности оценки налогового потенциала региона, которую дает описанная в работе система поддержки принятия решений, включающая совокупность оптимизационных математических моделей, алгоритмов их анализа и методов обработки экономической информации.