Плоская структура пространства – времени при относительно низких энергиях может быть нарушена пространственно – временной пеной квантовых флуктуаций. Этим флуктуациям соответствуют планковские кривизны и энергии фундаментальных полей материи, которые определяются планковской фундаментальной массой 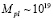 Гэв. В этом предположении структуры лагранжианов фундаментальных полей материи должны нарушаться членами, обратно пропорциональными Mpl.
Гэв. В этом предположении структуры лагранжианов фундаментальных полей материи должны нарушаться членами, обратно пропорциональными Mpl.
Действие для поля с учётом нарушающих симметрию плоского пространства членов достаточно хорошо описана в серии работ, начатой работой Майерса и Поспелова [1], а сами поля называются полями с нарушенной Лоренц – инвариантностью (LV). Этим полям соответствует растущий к планковским кривизнам пространства-времени энергетический спектр. Однако, результаты последних экспериментов наложили на LV теории очень сильные экспериментальные ограничения, которые заставляют сомневаться в возможности реализации этого механизма в доступном современным средствам наблюдения интервале энергий [2]. В то же время, в эксперименте GAP/IKAROS [3], повидимому, было обнаружено LV со спадающим с ростом энергии энергетическим спектром типа 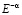 в диапазоне жёсткого рентгеновского излучения с энергией порядка 100 Кэв.
в диапазоне жёсткого рентгеновского излучения с энергией порядка 100 Кэв.
Назовём этот тип LV слабым нарушением Лоренц – инвариантности и попытаемся построить его в теории типа [1]. В ряде астрономических объектов при энергиях порядка < 1 Кэв обнаружено присутствие фрактальной материи на уровне флуктуаций [4]. В поступающих от этих объектов сигналах детектируется фрактальная составляющая также на уровне шумов. Предположим, что при более высоких энергиях вакуум электромагнитного поля слабо нарушен. Этому соответствует появление в его лагранжиане дифференциальных структур, задаваемых операторами малой размерности, которые задаются нецелыми производными 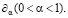
Пусть действие электромагнитного поля имеет вид:
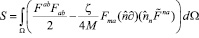 . (1)
. (1)
Здесь 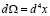 ,
, 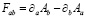 ; a,b=0..3; z – малый параметр, M –массовый параметр,
; a,b=0..3; z – малый параметр, M –массовый параметр,
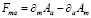 ,
,
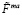 =
=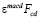 – дуальный тензор электромагнитного поля,
– дуальный тензор электромагнитного поля,
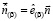 – оператор возведения производной
– оператор возведения производной 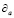 в нецелую степень
в нецелую степень 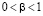 .
.
Единичный вектор 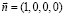 ;
; 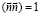 .
.
Так что, 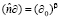 – нецелая производная по времени
– нецелая производная по времени 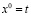 .
.
Оператор нецелой частной производной Риса по координате «x» имеет вид [5]:
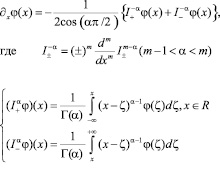 (2)
(2)
При 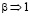 этот лагранжиан переходит в лагранжиан Майерса –Поспелова [1].
этот лагранжиан переходит в лагранжиан Майерса –Поспелова [1].
Варьируя функционал (1) по переменной Aa в калибровке Лоренца 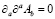 , получаем уравнения движения:
, получаем уравнения движения:
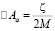
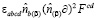 (3)
(3)
Пусть свободная плоская волна распространяется вдоль оси «z» (3). Тогда она поляризована в плоскости (XY) – (1,2).
Вектор поляризации волны имеет вид:
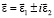 . (4)
. (4)
Уравнение (3) в компонентах есть:
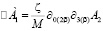 , (5)
, (5)
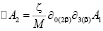 , (6)
, (6)
где 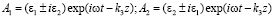 (7)
(7)
Спроектируем амплитуды волновых векторов в выбранном поляризационном базисе на координатные оси, используем фурье-образы для нецелых производных Риса от плоских волн [5] 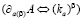 .
.
Получим дисперсионные соотношения:
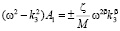 ,
, 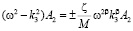 (8)
(8)
Оба эти уравнения в единой векторной форме в исходном пространстве полевых функций можно записать в форме
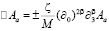 . (9)
. (9)
С учётом малости отношения 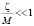 , получаем для частоты ω приближённое решение:
, получаем для частоты ω приближённое решение:
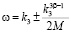 . (10)
. (10)
Обобщая соотношение (10) на произвольно движущуюся волну, получим
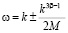 . (11)
. (11)
Здесь 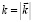 .
.
Учтём, что измерения производятся в гравитационном поле стандартной модели Вселенной с метрикой пространства – времени
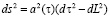 , (12)
, (12)
где безразмерные координата и время выбраны как
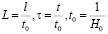 (
(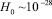 ) см – постоянная расширения вселенной Хаббла).
) см – постоянная расширения вселенной Хаббла).
В этой метрике обобщённые ковариантно частота 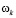 и импульс P световой волны примут вид:
и импульс P световой волны примут вид:
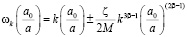 ,
, 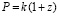 . (13)
. (13)
Поправка к частоте волны за счёт взаимодействия с вакуумом фрактальной материи, таким образом, имеет вид:
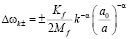 , (14)
, (14)
где константа LV нарушения выбрана как 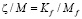 ,
, 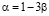 .
.
Предположим, что источник излучения находится от земного наблюдателя на расстоянии с красным смещением 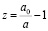 . Он генерирует волну, содержащую как суперпозицию левой (LP) и правой (RP) поляризаций, так и правую циркулярную поляризацию (CPR). Тогда волна потенциала поля может быть представлена в виде суперпозиции [6]:
. Он генерирует волну, содержащую как суперпозицию левой (LP) и правой (RP) поляризаций, так и правую циркулярную поляризацию (CPR). Тогда волна потенциала поля может быть представлена в виде суперпозиции [6]:
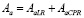 (15)
(15)
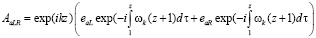 (16)
(16)
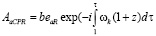 . (17)
. (17)
Параметр b в (15) – (17) является числовым параметром смешивания лево и право поляризованного излучения источника, векторы поляризации определены как
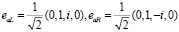 (18)
(18)
Вектор – потенциал волны (15) можно теперь переписать в явном виде
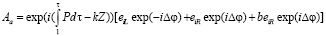 , (19)
, (19)
где 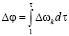 – фаза смешивания поляризаций.
– фаза смешивания поляризаций.
Следуя [6], ужесточим калибровку поля волны до унитарной (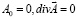 ,
, 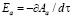 ) и рассчитаем компоненты электромагнитного поля детектируемой приёмником излучения волны Ea:
) и рассчитаем компоненты электромагнитного поля детектируемой приёмником излучения волны Ea:
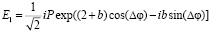 ; (20)
; (20)
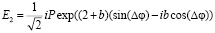 ; (21)
; (21)
Пользуясь выражениями для полей (20) – (21), можно рассчитать все характеристики излучения, которые детектируются в спутниковых экспериментах типа IBIS/FERMI, GAP/IKAROS [2, 3].
Необходимо сделать несколько замечаний относительно увязки формы спектра энергии (14) с методикой обработки результатов поляризационных экспериментов. Эта методика является модельно зависимой. Сначала отождествляются события, которые можно связать с поворотом плоскости поляризации электромагнитной ∆j волны при её распространении в пространстве. Потом эти события подставляются в растущую с ростом энергии E=ωk формулу Майерса – Поспелова, которая соответствует целым производным в формуле (1) →b=1. Получается, что плоскость поляризации излучения не вращается, левые фотоны не обгоняют правые. Тогда регистрируемое приборами излучение является неполяризованным. Поэтому, на параметр LV 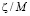 накладываются очень жёсткие ограничения
накладываются очень жёсткие ограничения 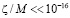 .
.
Эти жёсткие ограничения заставляют искать способ ослабления LV нарушения в стандартном геометрическом механизме [1]. При дробном механизме LV удаётся подобрать константы 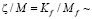 Mэв таким образом, чтобы этот геометрический эффект генерировал понижающийся с энергией спектр поляризованного излучения. Именно такой спектр измерен поляриметром GAP аппарата IKAROS в японском эксперименте по детектированию жёсткого поляризованного рентгеновского излучения гамма – всплесков [3].
Mэв таким образом, чтобы этот геометрический эффект генерировал понижающийся с энергией спектр поляризованного излучения. Именно такой спектр измерен поляриметром GAP аппарата IKAROS в японском эксперименте по детектированию жёсткого поляризованного рентгеновского излучения гамма – всплесков [3].
В предлагаемой теоретической модели оценим степень поляризации электромагнитного излучения гамма – всплесков, измеренную в эксперименте GAP [3]. Предположим, что спектральная плотность излучения гамма – источника в рентгеновском диапазоне даётся выражением
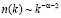 . (22)
. (22)
Согласно [3], степенной спектр источника GRB 110721A с таким показателем α типичен для физики космических лучей.
Будем считать, что поляризованное рентгеновское излучение исходит от фрактальной части материи источника.
Среднее значение
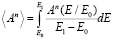 (23)
(23)
линейной поляризации пакета волн, принимаемых от источника излучения, при выбранных параметрах в пределах спектрального интервала 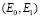 имеет вид:
имеет вид:
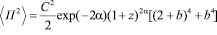 . (24)
. (24)
Это выражение необходимо нормировать на средний квадрат мощности принимаемого волнового пакета
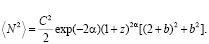 (25)
(25)
Для графического оформления результатов введём также безразмерную энергию 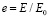 .
.
Измеряемая поляриметром линейная поляризация излучения есть
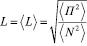 . (26)
. (26)
Подставляя (24), (25) в (26), получим
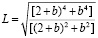 . (27)
. (27)
В [27] выявлен нелинейный оптический эффект по параметру b в излучении гамма – всплеска. Этот параметр не зависит от красного смещения z. Как видно из построенного по (27) рисунку, параметр L минимален при значении b=1. При этом, 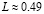 . По данным эксперимента GAP/IKAROS [3] L>0.35. То есть, имеет место достаточно хорошее совпадение результатов теории и эксперимента.
. По данным эксперимента GAP/IKAROS [3] L>0.35. То есть, имеет место достаточно хорошее совпадение результатов теории и эксперимента.
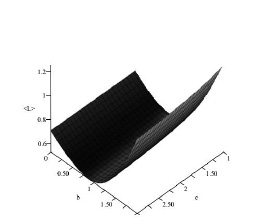
Зависимость поляризации L излучения гамма-всплеска от приведённой энергии e1 и параметра смешивания b

