Методы планирования размера выборки базируются на предположении, что к окончанию наблюдения будет возможно подтвердить или опровергнуть наличие предполагаемых различий между исследуемыми группами. Шанс выявления статистически значимых различий зависит от размера выборки и величины истинного различия сравниваемых показателей. Если в исследование включено небольшое количество пациентов и при этом не выявлен эффект, то встает вопрос, с чем это связано – с недостаточностью данных, или действительным отсутствием разницы. С другой стороны, неоправданное увеличение размера выборки неэффективно с точки зрения финансовых, трудовых и организационных затрат.
Целью статьи было представить способы расчёта оптимального объема выборки при планировании различных видов исследований.
Материалы и методы исследования
В данной работе предлагается обзор статистических методов расчета оптимального объема выборки. Были использованы следующие величины [3]:
Мощность критерия – способность критерия обнаружить статистически значимые различия, если они действительно существуют. Планируя исследование необходимо знать мощность используемого критерия. Имеет смысл начинать исследование, когда есть хороший шанс обнаружить клинически значимые различия. И нет смысла тратить ресурсы на 40 % вероятность подтверждения эффекта нового лечебного средства. Обычно мощность выбирается на уровне 70-80 % (β = 0,2 – 0,3).
Уровень значимости α задается самим исследователем. В настоящее время для клинических исследований рекомендуют выбирать альфа 0,01 или даже 0,001.
Вариабельность наблюдений, например, стандартное отклонение (дисперсия) для количественных признаков. Оценка дисперсии признака до начала исследования представляет собой определенную трудность. В качестве рекомендаций можно посоветовать воспользоваться ранее опубликованными данными по интересующей вас проблеме, или же самостоятельно провести небольшое пилотное исследование.
Наименьший клинически значимый эффект – минимальные изменения, которые мы не хотим игнорировать. Выбор его также лежит на исследователе, на его компетентности в сфере решаемой проблемы. Например, изучая реакцию на физическую нагрузку, нужно определить будет ли минимально клинически значимым изменение пульса на 5 уд/мин или же на 10 уд/мин, или же какое-то иное значение.
Результаты исследования и их обсуждение
Для сравнения количественного показателя в двух равновеликих независимых группах объем каждой выборки рассчитывается по формуле:
,
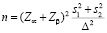где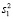 
и 
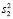– дисперсии признака в обеих группах; Δ – минимальная (клинически значимая) величина различий, которую необходимо обнаружить; Za и Zb – критические значения нормального стандартного распределения для заданных α и β (односторонний или двусторонний тест, в зависимости от формулировки альтернативной гипотезы), определяются по табл. 1 [1].
Таблица 1
Критические значения Z стандартного нормального распределения
|
Уровень знач. |
0,005 |
0,01 |
0,012 |
0,02 |
0,025 |
0,05 |
0,1 |
0,15 |
0,2 |
0,25 |
0,3 |
|
Одностор. тест |
2,567 |
2,326 |
2,257 |
2,054 |
1,96 |
1,645 |
1,282 |
1,036 |
0,842 |
0,674 |
0,524 |
|
Двусторон. тест |
2,807 |
2,576 |
2,513 |
2,326 |
2,242 |
1,960 |
1,645 |
1,440 |
1,282 |
1,150 |
1,036 |
Иногда по финансовым, этическим или другим причинам исследователь ограничен в своих возможностях набрать группу достаточной численности (как правило, это касается опытной группы). Если известна фиксированная численность одной выборки n1, то численность другой определяется следующим образом:
.
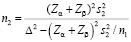Если сравниваются доли p1 и p2, частота встречаемости номинального признака, то объем выборки:
.
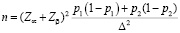здесь Δ – минимальная клинически значимая разница между долями; p1 и p2 определяется основываясь на подобных исследованиях из литературных источников, или на основе пилотного проекта. Как крайний случай можно выбрать p1=0,5 и p2=0,5, при этом численность выборки будет неоправданно завышена.
Если доля определена в %, то в выражении вместо 1 берется 100.
Такой метод дает достаточно точные результаты при 0,25<p<0,75. В других случаях вводится поправка
.
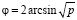При этом объем выборки:
.
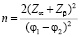Если объем одной выборки фиксирован, то объем второй
.
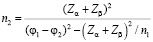Расчет объема выборки при эпидемиологических исследованиях
Вид выборки. Простая случайная выборка (простой рандомизированный отбор). При этом любая единица выборки имеет равные шансы быть отобранной с помощью жеребьевки, таблиц или компьютерного генератора случайных чисел.
Известна численность генеральной совокупности. Обычно эти данные можно получить из результатов переписи населения, отчетности статорганов, в которых указывается возрастной, половой, социальный и т.д. состав определенного региона (района, города, страны).
Для количественных признаков
.
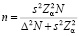где N – объем генеральной совокупности; Δ – ошибка выборки – это объективно возникающее расхождение между характеристиками выборки и генеральной совокупности, также как и уровень значимости ошибка выборки задается самим исследователем. Ее предварительная оценка (предпочитаемая величина перед подстановкой в формулу) часто произвольна. Как правило, не рекомендуется принимать ошибку выборки выше 5 % [2].
Для номинальных и порядковых признаков (доли объектов с заданным признаком)
.
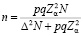где q=1–p,
p подбирается эмпирическим путем, или как крайний случай p=0,5 и q=0,5
При неизвестной численности генеральной совокупности для количественных признаков
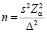
для случая определения доли
.
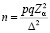Вид выборки. Стратифицированный способ отбора – все объекты разделяют на классы, именуемые слоями (стратами), в зависимости от изучаемых характеристик, таких как возраст, пол и т.п., после чего из каждого слоя отбирается простая случайная выборка с одинаковой или специально рассчитанной (для каждого слоя) выборочной долей
Объем генеральной совокупности известен
Признак количеcтвенный
Общий объем выборки определяется как
,
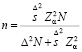где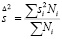 
– средняя внутригрупповая дисперсия; Ni – число объектов в каждом из классов генеральной совокупности
Тогда выборка из каждого класса имеет численность пропорциональную представительству в генеральной совокупности
.
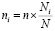Но более оптимальным является распределение выборки по классам с учетом вариабельности признака в этих классах
.
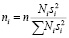Признак качественный (частота встречаемости)
,
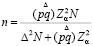где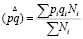 
– средняя внутригрупповая дисперсия,
где pi и qi – доля и обратная ей величина в каждом из классов генеральной совокупности (как крайний случай p=0,5 и q=0,5); Ni – число объектов в каждом из классов генеральной совокупности.
При неизвестной численности генеральной совокупности для количественных признаков
.
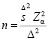для случая определения доли
.
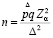Разделение общей выборки по классам также производится пропорционально или с определенным весом.
Следует обратить внимание, что если доля выражается в относительных единицах, то все расчеты также производятся в относительных единицах, если в процентах – то и другие величины выражаются в процентах.
Кроме приведенных формул существуют и другие способы определения численности выборки. Среди них специальные таблицы и диаграммы, а также компьютерные программы. Учитывая, что в течение исследования неизбежны потери среди его участников (по разным причинам), рекомендуется расчетный объем выборки увеличить примерно на 20 %.
Обычно исследованию подлежат не один, а несколько признаков (например, давление, ЧСС, температура, биохимические показатели и т.д.), и для каждого признака возможен свой уровень значимости, клинически значимые изменения и, соответственно, свой объем выборки. В этом случае исследователь может в качестве окончательного выбрать наибольшую из всех рассчитанных численностей, или же задать объем выборки, рассчитанный для главного признака – исходя из основной гипотезы.
Рассмотрим данные методики на примерах.
Пример 1. Необходимо определить объем выборки при сравнении общего состояния в двух группах по шкале качества жизни SF-36 (Short Form-36). Разница считается статистически значимой при р<0,05. Заданная мощность критерия 85 %, минимально значимая разница по шкале SF-36 составляет 5 баллов. По результатам предварительного исследования стандартное отклонение в первой группе 9,1 балл, во второй – 10,2 балла.
.
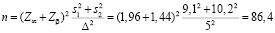С поправкой на возможность выбывания из исследования участников – 20 %, общий объем выборки составляет 86,4·1,2=104 участника, по 52 человека в каждой группе.
Пример 2. Рассчитаем объем выборки, необходимый для оценки урологической заболеваемости в некотором регионе с учетом того, что среди мужчин и женщин эта патология имеет различную распространенность. Общая численность взрослого населения в этом регионе (генеральная совокупность) составляет 1638240 человек, из них мужчин 735882 и женщин 902358 человек. По некоторым литературным данным урологические заболевания выявляются у 11,1 % мужчин и 10,7 % женщин (табл. 2).
Таблица 2
Сведения по урологической заболеваемости
|
Группа |
Ni |
pi, % |
qi=(100 – pi), % |
Δ, % |
Z |
|
Мужчины |
735882 |
11,1 |
88,9 |
1 |
2,576 |
|
Женщины |
902358 |
10,7 |
89,3 |
Нам необходимо сформировать стратифицированную выборку с учетом зависимости распространенности заболевания от пола. Т.к. ожидаемая доля невелика (~ 11 %) зададим ошибку доли 1 %.
Средняя внутригрупповая дисперсия
.
Общий объем выборки
чел.
При этом выборка мужчин
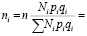
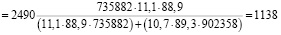чел.
Выборка женщин
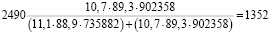чел.
Заключение
Таким образом, предложенные методы определения объема выборки могут быть использованы для расчета минимального объема выборочной совокупности на стадии планирования экспериментальных, клинических или эпидемиологических исследований.