Управление бюджетной системой Российской Федерации предопределяется новыми социально-экономическими подходами, обусловленными рыночными отношениями и соответствующей им институциональной структурой общества. Существование в организации общественно-экономической жизни механизмов местного самоуправления в рамках единой государственной системы отношений имплицировало использование, наряду с системно-ориентированым подходом к управлению, новых подходов ― подходов эволюционного управления, ориентированных на поддержку самоорганизующих тенденций. Одним из наиболее важных вопросов поддержания процессов функционирования такой системы с встроенным в неё местным самоуправлением является обеспечение её деятельности финансовыми ресурсами. Этот вопрос стоит в центре внимания муниципальных и государственных органов не только России. Опытом зарубежных стран подтверждается, что достаточность собственных бюджетных средств является непременным условием существования местного самоуправления. Таким образом, концепция управления бюджетной системой Российской Федерации базируется на сочетании двух подходов ― системно-ориентированного и эволюционного, предполагающих рассмотрение смешанной системы, использующей два полярных способа построения её структуры – иерархического, при котором все действия элементов структуры регламентированы инструкциями в системе отношений строгого подчинения, и гетерархического, при котором каждый элемент, руководствуясь как общими правилами, так и текущей ситуацией, берёт на себя инициативу управления в интересах всей структуры. Функционирование такой гибридной структуры приводит к поведенческой сложности объекта управления, характеризующейся присутствием различных, последовательно сменяющих друг друга во времени поведений. Многорежимный характер процессов функционирования объекта управления вызывает проблемы при их моделировании, а также при постановке задачи управления. Используемая при решении задач управления бюджетом математическая модель объекта управления (бюджета муниципального образования) должна содержать механизмы управляемого изменения взаимодействий с бюджетом регионального уровня, а также механизмы адаптации законов её функционирования к смене режимов поведения. В связи с этим авторами предложено абстрактное представление сложной динамики бюджетных потоков, проходящих через бюджеты бюджетной системы Российской Федерации, в виде преобразования алфавитов сложной динамической системой. Сложная динамическая система представлена семейством взаимосвязанных и взаимодействующих между собой математических объектов – динамических систем 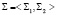 . Закон функционирования системы
. Закон функционирования системы 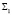 , воспроизводящей динамику проходящих через местный бюджет бюджетных потоков, а также динамику остатков денежных средств на расчётном счёте бюджета этого уровня, моделируется имитационной системой. Эта имитационная система формирует случайную среду, в которую погружены вероятностные автоматы, реализующие дискретную динамическую систему
, воспроизводящей динамику проходящих через местный бюджет бюджетных потоков, а также динамику остатков денежных средств на расчётном счёте бюджета этого уровня, моделируется имитационной системой. Эта имитационная система формирует случайную среду, в которую погружены вероятностные автоматы, реализующие дискретную динамическую систему 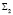 . Математический объект
. Математический объект 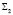 описывает поведение ЛПР в процессе принятия решений при бюджетном регулировании: осуществляет координацию бюджетных процессов муниципального уровня бюджетной системы РФ органами власти вышестоящего уровня посредством выбора оптимальных значений компонентов вектора состояний
описывает поведение ЛПР в процессе принятия решений при бюджетном регулировании: осуществляет координацию бюджетных процессов муниципального уровня бюджетной системы РФ органами власти вышестоящего уровня посредством выбора оптимальных значений компонентов вектора состояний 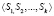 , обеспечивающих некоторое равновесие между интересами бюджетов этих уровней. Значения компонентов вектора состояний Si,
, обеспечивающих некоторое равновесие между интересами бюджетов этих уровней. Значения компонентов вектора состояний Si, 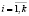 отражают величины нормативов отчислений в местный бюджет от федеральных и региональных налогов и сборов, подлежащих зачислению в бюджет субфедерации. Система
отражают величины нормативов отчислений в местный бюджет от федеральных и региональных налогов и сборов, подлежащих зачислению в бюджет субфедерации. Система 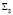 реализована в виде коллектива взаимодействующих стохастических автоматов, функционирующих в случайных средах. Авторами предложена конструкция стохастических автоматов [1], составляющих коллектив. Под конструкцией стохастического автомата понимается его функция переходов
реализована в виде коллектива взаимодействующих стохастических автоматов, функционирующих в случайных средах. Авторами предложена конструкция стохастических автоматов [1], составляющих коллектив. Под конструкцией стохастического автомата понимается его функция переходов 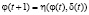 , задаваемая с помощью матриц переходов, и функция выходов
, задаваемая с помощью матриц переходов, и функция выходов 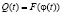 . Опишем эти функции. В качестве состояний автомата рассматривается вектор
. Опишем эти функции. В качестве состояний автомата рассматривается вектор 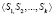 , компоненты которого Si,
, компоненты которого Si, 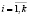 принимают значения нормативов отчислений в бюджет муниципального уровня от налога i-го вида, подлежащего зачислению в региональный бюджет бюджетной системы РФ. В качестве выходов Qi,
принимают значения нормативов отчислений в бюджет муниципального уровня от налога i-го вида, подлежащего зачислению в региональный бюджет бюджетной системы РФ. В качестве выходов Qi, 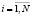 рассматривается величина остатков денежных средств, аккумулируемых в бюджете муниципального уровня бюджетной системы РФ. Автомат имеет два значения входной переменной δ, именуемой «штраф» при
рассматривается величина остатков денежных средств, аккумулируемых в бюджете муниципального уровня бюджетной системы РФ. Автомат имеет два значения входной переменной δ, именуемой «штраф» при 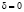 и «нештраф» при
и «нештраф» при 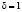 и погружён в стационарную случайную среду с вероятностными характеристиками, описываемыми вектором
и погружён в стационарную случайную среду с вероятностными характеристиками, описываемыми вектором 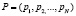 . Если в момент времени t автомат произвёл действие
. Если в момент времени t автомат произвёл действие 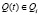 , то в момент (t+1) на его вход поступит сигнал
, то в момент (t+1) на его вход поступит сигнал 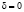 с вероятностью pi и
с вероятностью pi и 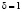 с вероятностью
с вероятностью 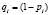 . Автомат A1 штрафуется (
. Автомат A1 штрафуется (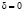 ), если величина текущего остатка денежных средств в бюджете
), если величина текущего остатка денежных средств в бюджете 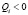 , т.е. если в бюджете возникает дефицит. Значение функции выхода автомата
, т.е. если в бюджете возникает дефицит. Значение функции выхода автомата 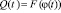 реализуется в процессе функционирования созданной автором имитационной системы
реализуется в процессе функционирования созданной автором имитационной системы 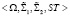 , где W – модель построения законов распределения случайной величины «доходы» и «расходы» бюджета;
, где W – модель построения законов распределения случайной величины «доходы» и «расходы» бюджета; 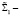 модель генерации возможных значений случайных величин;
модель генерации возможных значений случайных величин; 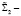 модель, осуществляющая формирование значений фазового состояния Q(t) (т.е. величин остатков денежных средств в местном бюджете) под действием входных и возмущающих воздействий, а также осуществляющая вычисление значений выходных сигналов p и q; Авторами предложена конструкция автомата, определяющая функцию перехода
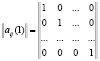
модель, осуществляющая формирование значений фазового состояния Q(t) (т.е. величин остатков денежных средств в местном бюджете) под действием входных и возмущающих воздействий, а также осуществляющая вычисление значений выходных сигналов p и q; Авторами предложена конструкция автомата, определяющая функцию перехода 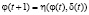 с помощью матриц переходов из состояния в состояние под действием входных сигналов
с помощью матриц переходов из состояния в состояние под действием входных сигналов 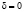 (матрица
(матрица 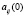 ) и
) и 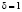 (матрица
(матрица 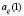 , имеющих вид выражений:
, имеющих вид выражений:
 ,
,
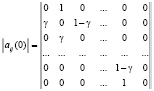
В этих выражениях g означает избирательность стратегии автомата при штрафе. Вероятность pij перехода автомата из состояния ϕi в состояние T определяется следующим образом: 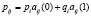 . Матрица переходных вероятностей
. Матрица переходных вероятностей 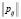 имеет вид:
имеет вид:
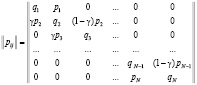
С использованием известных соотношений из теории стохастических автоматов, система уравнений для определения финальных вероятностей 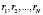 пребывания автомата в определённом состоянии запишется в виде:
пребывания автомата в определённом состоянии запишется в виде:
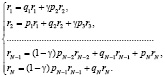
Решение системы уравнений позволяет получить выражения для финальных вероятностей ri,  пребывания автомата в своих состояниях, используемых в модели коллективного поведения автоматов [2], определяющей компромиссные варианты решений при долевом распределении налогов между уровнями бюджетной системы.
пребывания автомата в своих состояниях, используемых в модели коллективного поведения автоматов [2], определяющей компромиссные варианты решений при долевом распределении налогов между уровнями бюджетной системы.

