Настоящее сообщение является выдержкой из монографии автора «Последняя теорема Ферма: неоконченная история», издать которую не представляется пока возможным по финансовым соображениям. Однако важность и перспективность полученных результатов не терпят, как говорят в таких случаях, отлагательств. Поэтому здесь в краткой форме будут изложены некоторые основные моменты нового подхода как в вычислительной математике, так и в физической квантовой теории.
Прежде всего следует отметить, что знаменитая теорема Ферма (далее: ВТФ) затрагивает самые существенные, основополагающие элементы наших знаний о природе вещей. После исследований [1-8] стало ясно, что ВТФ - это не какая-то там шарада для заформализованных математиков, а это настоящее откровение о сущности нашего мира, выраженное в математической форме. Причем выясняется, что без такого откровения никакой истинный постапокалиптический прогресс человечества невозможен [4-5]. Разобраться в этом историческом послании от Ферма хотя бы в первом приближении может теперь каждый здравомыслящий человек с минимальными познаниями в объеме вузовской математики [7].
Единственное препятствие этому - консервативное (если не сказать больше!) и высокомерное отношение высоких математических кругов к знаниям, полученным не зависимым от них способом [3]. От этого страдают не только молодые ученые, привыкшие доверять корпоративным научным авторитетам, но, главное, учащаяся молодежь, подпавшая под дурман устаревших догматических установок средней и высшей школы [6].
Сформулируем теперь ВТФ в терминах квантовой информатики. Основными единицами квантовой информации являются кубиты (квантовые биты). Кубиты материализуются в виде спиновых (псевдоспиновых) систем, находящихся в едином информационном поле, являющемся одновременно и физическим полем (с частицами или без них). ВТФ описывает универсальную закономерность распределения кубитов для систем, состоящих из одинаковых спиновых (псевдоспиновых) подсистем с n различными частицами в каждой (назовем эти n-частичные подсистемы при n ≥2, объединенные между собой резонансным взаимодействием двух альтернативных состояний, квантовыми комплексами, см. рис.1). В такой кубитной интерпретации целых чисел справедлива следующая теорема:
Любое целое число комплексов симметричного физического вакуума, изображаемое целой степенью zn , при любом натуральном n≥3 входящих в каждый комплекс частиц всегда состоит из трех ансамблей, находящихся в трех независимых состояниях - двух альтернативных чистых и перепутанном. При этом доля этих ансамблей в каждый момент времени выражается целым (или рациональным при нормировке на zn) числом, включая рациональное число 0, причем альтернативные чистые (условно назовем их «начальное» и «конечное») состояния комплексов выражаются целыми степенями, а перепутанные состояния - просто целым (рациональным) числом без степени.
Арифметически эта теорема записывается так же, как и позитивная формулировка ВТФ [5]: zn = xn + yn + ln , где zn - любая целая степень квантовых комплексов при резонансном в них взаимодействии (т.е. при сохранении физической информации в каждом комплексе), z, x, y - числа одинаковых частиц в плотностях кубитов zn, xn, yn; n - число различных частиц в каждом комплексе (см. рис.2 и расчетные диаграммы в [1]); xn - доля одного из альтернативных чистых состояний системы в целых числах, yn - доля другого альтернативного чистого состояния системы в целых числах (сумма долей xn и yn описывает смесь альтернативных чистых состояний квантовой системы); ln - доля перепутанных состояний системы в целых числах. Таким образом, комплексы, находящиеся в перепутанных состояниях, можно теоретически пересчитать по теореме Ферма «поштучно».
Применяя метод матрицы плотности, описывающий эволюцию квантовой системы во времени, к расчету вероятностей состояний резонансной квантовой системы, состоящей из двух или более подсистем, приходим к аналогичному выражению для нормированной к 1 плотности состояний консервативной (не взаимодействующей со своим окружением) системы [8]: ρ =ρ11 + ρ12 + ρ21 + ρ22 = 1 , где ρ11 и ρ22 - плотности альтернативных резонансных состояний квантовой системы (смесь чистых состояний); ρ12 и ρ21 - плотности перепутанных состояний, представленные комплексно сопряженными числами. Для двухчастичных резонансных комплексовρ12 + ρ21 = 0, для многочастичных комплексов (при n≥3) ρ12 + ρ21≠0. Кроме того, полный учет всех элементов матрицы плотности дает также новые решения для полевых волн-частиц, ответственных за образование и динамику перепутанных состояний квантовой системы [8]. Эти решения инстантонного типа были названы автором инвертоном и
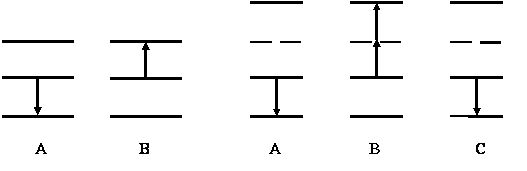
Рис. 1. Обобщенные энергетические схемы квантовых кооперативных процессов в резонансных комплексах из двух А и В и трех А, В, С частиц: сплошные горизонтальные линии - реальные уровни энергии; пунктирные линии - пример виртуальных уровней из бесконечного их набора; стрелками показан момент кросс-релаксационного псевдоспинового электронного перехода.

Рис. 2. Пример схем возбуждения в симметричном вакууме zn
виртуальных комплексов, состоящих из n разных частиц и изображаемых
симметричными графами для случаев, когда
n = 2, 3, 4. Все ребра графа направлены только в какую-либо одну сторону (либо
вправо, либо влево), что согласуется с условиями задачи, по которым частицы
одного сорта не могут взаимодействовать ни с самими собой, ни с себе подобными.
В образовании каждого комплекса участвуют только те вершины графа, которые
представляют частицы разных сортов. Ребра графа не являются расстояниями, т.е.
не отвечают метрическим представлениям, и, следовательно, все zn
комплексов помещаются в одной точке физического пространства. Тем не менее,
подобная нейросеть (от греческого слова «нейрон», что значит «жила») позволяет
информационно наглядно и быстро подсчитать все слагаемые позитивной теоремы
Ферма (см. текст).
антиинвертоном [5]. В результате получаем, что квантовый расчет плотностей состояний квантовой системы по теореме Ферма, т.е. когдаρ11= xn/zn, ρ22= yn/zn, ρ2 + ρ21 = λn/zn, содержит в себе более наглядную и более реалистичную картину процессов, происходящих в физическом вакууме, чем аналоговое их описание с помощью волновых функций или классических матриц вращения (поворотов).
СПИСОК ЛИТЕРАТУРЫ:
1. Ивлиев Ю.А. Великая теорема Ферма с точки зрения физика (о некоторых квантово-полевых моделях счета) - Сверхпроводимость: исследования и разработки 1995 № 5-6, 5-16. ISSN 0868-8885.
2. Ивлиев Ю.А. Реконструкция нативного доказательства Великой теоремы Ферма - Объединенный научный журнал (раздел «Математика») 2006 № 7 (167), 3-9. ISSN 1729-3707.
3. Ивлиев Ю.А. Величайшая научная афера ХХ века: «доказательство» Последней теоремы Ферма - Естественные и технические науки (раздел «История и методология математики») 2007 № 4 (30), 34-48. ISSN 1684-2626.
4. Ивлиев Ю.А. Великая теорема Ферма и современные математические науки - Научное обозрение. М.: Наука 2009 № 2, 53-55. ISSN 1815-4972.
5. Ивлиев Ю.А. Великая теорема Ферма и современная наука - Фундаментальные исследования (раздел «Материалы V Общероссийской научной конференции «Актуальные вопросы науки и образования»») 2009 № 5, 14-16. ISSN 1812-7339.
6. Ивлиев Ю.А. О качестве преподавания математики учащейся молодежи - Успехи современного естествознания (раздел «Материалы общероссийской научной конференции «Перспективы развития вузовской науки») 2009 № 10, 53-55. ISSN 1681-7494.
7. Ивлиев Ю.А. Разгадка феномена Великой теоремы Ферма - Фундаментальные исследования (раздел «Педагогические науки») 2010 № , . ISSN 1812-7339.
8. Ivliev Y.A. Quantum and Pseudoquantum Teleportation as Effects of Generalized Relativistic Mechanics - Engineering & Automation Problems 2000 # 1, 68-71. ISSN 0234-6206.
