В настоящее время итоговая аттестация выпускников школ проводится в формате единого государственного экзамена (ЕГЭ). Задания, предлагаемые в качестве контрольно-измерительных материалов, из года в год претерпевают изменения. Есть задания, с которыми учащиеся справляются без затруднений, но есть задания, которые вызывают у учащихся значительные трудности. К таким заданиям можно отнести задания С5 и С6.
Наш опыт показывает, что возможно, вооружив учащихся необходимым учебным материалом, облегчить решение таких заданий. Остановимся в данной статье на одной теореме, которая может стать подспорьем в решении трудных задач ЕГЭ по математике, в частности, задач С5, предложеных в 2013 году.
Теорема. Пусть задано уравнение f(h(x))=f(g(x)). Если функция f монотонна, то заданное уравнение на своей области определения равносильно уравнению h(x)=g(x).
Рассмотрим решение уравнения 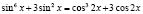 , применив для этого сформулированную теорему.
, применив для этого сформулированную теорему.
Рассмотрим функцию 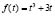 . Если мы в данную функцию вместо t подставим sin2x, то получим левую часть уравнения, а если cos2x, то получим правую часть уравнения. Значит, заданное уравнение имеет вид f(sin2x)=f(cos2x). Исследуем функцию f(t) на монотонность, для чего найдем ее производную. Будем иметь:
. Если мы в данную функцию вместо t подставим sin2x, то получим левую часть уравнения, а если cos2x, то получим правую часть уравнения. Значит, заданное уравнение имеет вид f(sin2x)=f(cos2x). Исследуем функцию f(t) на монотонность, для чего найдем ее производную. Будем иметь:
f′(t) = 3t2+3. Так как f′(t) >0, то функция f(t) монотонно возрастает. Тогда заданное уравнение, согласно теореме, будет равносильно уравнению sin2x=fcos2x. Его решение довольно простое, а потому мы его приводить не будем.
В 2013 году в качестве С5 учащимся были предложены задания:
Задание 1. Найдите все значения параметра  , для каждого из которых уравнение
, для каждого из которых уравнение 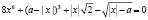 имеет более трех различных корней.
имеет более трех различных корней.
Задание 2. Найдите все значения параметра 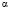 , для каждого из которых уравнение
, для каждого из которых уравнение 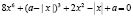 имеет более трех различных корней.
имеет более трех различных корней.
Задание 3. Найдите все значения параметра 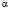 , при которых уравнение
, при которых уравнение  имеет более одного корня.
имеет более одного корня.
Рассмотрим решение задания 1. Запишем заданное уравнение в виде 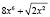
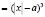 +
+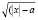 . Рассмотрим функцию f(t)=
. Рассмотрим функцию f(t)=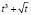 . Если мы в данную функцию вместо t подставим
. Если мы в данную функцию вместо t подставим 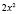 , то мы получим левую часть уравнения, а если
, то мы получим левую часть уравнения, а если 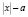 , то получим правую часть уравнения. Значит, заданное уравнение имеет вид f(
, то получим правую часть уравнения. Значит, заданное уравнение имеет вид f(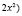 =f(|x|–a) Легко показать, что производная
=f(|x|–a) Легко показать, что производная 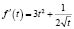 всегда положительна, а значит функция f(t) монотонно возрастает. Тогда заданное уравнение, согласно теореме, будет равносильно уравнению
всегда положительна, а значит функция f(t) монотонно возрастает. Тогда заданное уравнение, согласно теореме, будет равносильно уравнению 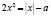 . Решим его графически, для чего вначале запишем его в виде
. Решим его графически, для чего вначале запишем его в виде 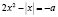 , или
, или 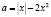 ,
,
или 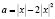 . В одной системе координат построим графики функций
. В одной системе координат построим графики функций 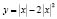
и y =а. Мы увидим, что при 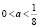 прямая y =а пересекает график функции
прямая y =а пересекает график функции 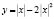 в четырех точках. Следовательно, ответом служит промежуток
в четырех точках. Следовательно, ответом служит промежуток 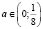 .
.
Рассмотрим решение задания 3. Запишем заданное уравнение в виде 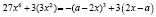 , или
, или 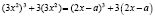 . Рассмотрим функцию
. Рассмотрим функцию 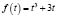 . Если мы в данную функцию вместо t подставим
. Если мы в данную функцию вместо t подставим 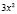 , то мы получим левую часть уравнения, а если
, то мы получим левую часть уравнения, а если 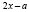 ,
,
то получим правую часть уравнения. Значит, заданное уравнение имеет вид 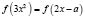 Производная
Производная 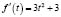 всегда положительна, а значит функция f(t) монотонно возрастает. Тогда заданное уравнение, согласно теореме, будет равносильно уравнению
всегда положительна, а значит функция f(t) монотонно возрастает. Тогда заданное уравнение, согласно теореме, будет равносильно уравнению 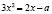 , или
, или 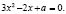 Квадратное уравнение будет иметь более одного корня (слова «более одного корня» следует понимать как два различных корня), если его дискриминант положителен: D = 4–12а > 0, откуда
Квадратное уравнение будет иметь более одного корня (слова «более одного корня» следует понимать как два различных корня), если его дискриминант положителен: D = 4–12а > 0, откуда 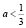 .Следовательно, ответом служит промежуток
.Следовательно, ответом служит промежуток 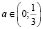 .
.
Аналогичным образом можно решить и задание 2.
Покажем приемы, которые можно использовать для рационализации неравенств.
Для рационализации неравенств можно использовать следующие замены выражений:
а) 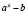 на
на 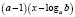 ;
;
б) 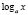 на
на 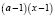 ;
;
в) 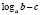 на
на 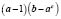 ;
;
г) 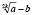 на
на 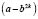 .
.
Как правило, a, b, c являются функциями. Не сложно доказать справедливость указанных замен.
Каждая из указанных замен приводит обычно к изменению области допустимых значений (ОДЗ), причем, и это очень важно, ОДЗ нового неравенства шире, чем у исходного, так что потери решений не происходит, а полученные в конце решения надо еще проверить на вхождение в ОДЗ исходного неравенства. Другими словами, решениями исходного неравенства будут те из полученных решений, которые лежат в его ОДЗ, в таком случае мы будем говорить, что новое неравенство равносильно исходному в его ОДЗ. Следовательно, надо начинать решения с нахождения ОДЗ исходного неравенства. Заметим также, что когда a, b, c зависят от х, получаемое после замены неравенство вовсе не обязательно будет рациональным.
Рассмотрим три примера.
а) Решить неравенство
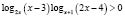 .
.
Решение. Найдем область определения неравенства:
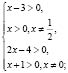
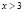
Воспользуемся заменой, указанной под буквой а). Будем иметь:
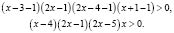
Используя метод интервалов и учитывая область определения исходного неравенства, получим х>4.
б) Решить неравенство:
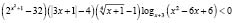 .
.
Решение. Найдем область определения исходного неравенства:
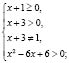
получаем 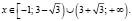
Используя указанные выше замены а) – г), получаем:
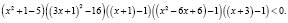
Решение этого неравенства уже не представляет сложности, но не следует забывать про область определения исходного неравенства.
в) Решить неравенство: 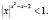
Решение. Областью определения исходного неравенства являются все действительные числа, кроме нуля.
Перепишем неравенство в виде 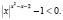 Используя указанные замены а) и г), получим
Используя указанные замены а) и г), получим
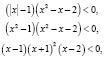
откуда, методом интервалов, находим ответ 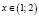 .
.
Аналогичные рекомендации, облегчающие решение уравнений, можно дать и по отношению к уравнению вида 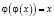 , где
, где 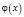 – некоторая функция.
– некоторая функция.
Примерами таких уравнений могут быть:
а) 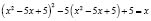
б) 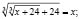
в) 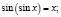
г) 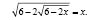
Рекомендации по решению уравнений вида 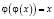 приведены в нашей работе [1].
приведены в нашей работе [1].
Рекомендации, облегчающие решение, можно дать и по отношению к уравнению вида
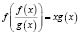 ,
,
где f(x), g(x) – некоторые функции. Заметим, что это уравнение является обобщением класса уравнений 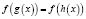 .
.
Для указанного уравнения
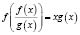
справедливы следующие утверждения, полезные при их решении.
1. Корни уравнения
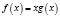 , (*)
, (*)
входящие в область допустимых значений уравнения
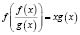 , (**)
, (**)
являются решениями уравнения (**).
2. Если функция f(x) возрастающая
и g(x) > 0, или функция f(x) убывающая
и g(x) < 0 на области допустимых значений уравнения (**), то уравнения (**) и (*) равносильны на области допустимых значений уравнения (**).
3. Если функция f(x) является многочленом n-й степени и g(x) – многочлен, то полином
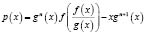
делится на многочлен 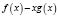 .
.

