Scientific journal

International Journal of Applied and fundamental research

ISSN 1996-3955

ИФ РИНЦ = 0,593

Модернизация промышленности невозможна без внедрения новейших технологий и оборудования, обеспечивающих выпуск конкурентоспособной продукции по качественным и экономическим показателям. Разработчики передовых технологий и оборудования используют эффективные методы научных исследований, что дает возможность сократить продолжительность и стоимость решения поставленных задач.

К таким эффективным методам в первую очередь следует отнести математизацию исследований.

Математизация исследований, а, следовательно, и тех областей знания, к которым принадлежат эти исследования, предполагает в первую очередь получение математической модели исследуемого процесса, достаточно точно, адекватно его описывающей. При наличии такой модели возникает возможность заменить дальнейшее исследование процесса анализом его математической модели для решения поставленных конкретных задач [1].

Мир по своей природе сложен и многомерен. При этом в природе (равно как и во всех естественных науках) все находится во взаимосвязи и взаимозависимости. Это означает, что многие показатели, даже не будучи связаны между собой формализованными алгоритмами, тем не менее, изменяются в динамике согласованно.

Математическое прогнозирование и моделирование тех или иных химических процессов, оценку отсутствующих (дефицитных) характеристик физико-химических систем позволяет осуществить метод многоуровневого моделирования (ММУМ). Применяя метод многоуровневого моделирования, можно ограничиться предположением, что функция от нескольких параметров выражается системой линейных уравнений. При этом необходимо осуществить обоснованный выбор базисных параметров. Так, например, установлено, что при изучении свойств растворителей (где каждая частица вносит свой вклад в изменение свойств всей системы) достаточно ограничиться четырьмя базисными параметрами [2].

В данной работе методом многоуровневого моделирования была получена математическая модель, характеризующая дубящую дисперсную систему.

Разработка технологии получения дубящих дисперсных систем ведется с целью создания инновационной технологии намазного дубления кож. Внедрение этой технологии в производство позволит получать конкурентоспособную продукцию (полуфабрикат Wet-blue) при значительном сокращении расхода ресурсов (химических материалов, воды, электроэнергии, производственных площадей и т.д.) и снижении антропогенной нагрузки на окружающую среду.

Дубящие дисперсные системы представляют собой (предельно) высококонцентрированные дисперсные системы, стабилизированные поверхностно-активным веществом (ПАВ). Дисперсная фаза представляет собой концентрированный водный раствор основных солей хрома (III), в качестве дисперсионной среды были использованы жирующие композиции, применяемые в кожевенно-меховой промышленности. Дисперсные системы для намазного дубления кож должны обладать следующими технологическими характеристиками: достаточная агрегативная устойчивость и вязкость, содержание жирующего материала (дисперсионной среды) не должно превышать 5 %.

Известно, что свойства дисперсных систем зависят от большого количества факторов. Все эти факторы можно разделить на две основные группы: сила и энергия сцепления (взаимодействия) в контактах между частицами дисперсных фаз, а так же число контактов между ними в единице объема. При этом сила и энергия взаимодействия в контактах между частицами зависят от вида (природы) контактов, химической природы, формы и состояния поверхности частиц дисперсных фаз, химического состава и физических свойств дисперсионной среды [3].

В работе [4] было показано, что состав и свойства дисперсионной среды оказывают значительное влияние на изменение характеристик дубящих дисперсных систем.

Современный рынок материалов для производства кожи и меха характеризуется разнообразием предлагаемой продукции. Кроме того, нередко отдельные материалы могут быть сняты с производства. Все это затрудняет выбор компонентов для производства дубящих дисперсных систем, является препятствием для разработки технологии получения дисперсных систем с заданными свойствами.

В связи с этим необходимо провести подробное изучение закономерности изменения свойств дисперсной системы при изменении физико-химических свойств ее компонентов. С этой целью в работе методом многоуровневого моделирования была получена и проанализирована математическая модель, выражающая зависимость характеристики дисперсной системы (минимальное содержание дисперсионной среды) от физико-химических свойств жирующих композиций и ПАВ, применяемых при ее получении.

В качестве дисперсионной среды были исследованы следующие жирующие композиции: Derminol CNS, Derminol ALE, Derminol CFS, Drminol CTS. Все композиции представляют собой сульфитированные натуральные и синтетические жиры и масла. В качестве эмульгаторов и стабилизаторов системы использовали композиции на основе анионактивных веществ: Tergolix D, Tergolix-W-01, De-sol-a и LOC.

Приготовление дубящих дисперсных систем проводилось путем постепенного введения водного раствора основных солей хрома (III) в смесь жирующего материала и ПАВ (взятых в соотношении 1:1 по массе сухого вещества). Подача дубителя осуществлялась при постоянном перемешивании с помощью микроразмельчителя тканей РТ-2 (3000 об./мин.). Подача дубителя осуществлялась до начала разрушения состава, которое фиксировалось по появлению первых объемов дубителя, выделяющихся из системы. Объем внедренного раствора использовали для расчета минимального содержания дисперсионной среды в дисперсной системе (Y, %) (изучаемая характеристика).

В качестве параметров моделирования для описания характеристики сложной многокомпонентной дисперсной системы были выбраны следующие химические и физико-химические свойства ее компонентов:

- содержание сухого остатка в композиции на основе ПАВ (Х₁, %), определенное гравиметрическим методом (обезвоживание навески проводилось в эксикаторе над периодически просушиваемым хлоридом кальция);

- относительная (условная) вязкость композиции на основе ПАВ (Х₂, усл.ед.), определенная как отношение времени истечения композиции к времени истечения воды из отверстия вискозиметра;

- содержание анионактивных ПАВ в композиции, считая на сухое вещество
(Х₃, %), определенное оптическим методом (с помощью калибровочного графика по додецилсульфату натрия);

- критическая концентрация мицеллообразования (ККМ) (Х₄, мг/дм³), определенная из графика зависимости σ = f(C), где σ определена сталагмометрическим методом;

- содержание сухого остатка в жирующей композиции (Х₅, %), определенное гравиметрическим методом (обезвоживание навески проводилось в эксикаторе над периодически просушиваемым хлоридом кальция);

- относительная (условная) вязкость жирующей композиции (Х₆, усл.ед.), определенная как отношение времени истечения композиции к времени истечения воды из отверстия вискозиметра;

- йодное число жира (Х₇, г на 100 г сухого жира), определенное титриметрическим методом

- отношение площади пика связи S=O к площади пиков групп -СН₃ и -СН₂- (Х₈, %), определенное из спектра поглощения жирующей композиции, полученного с помощью ИК-спектрометра Фурье.

Исходные данные для многоуровневого моделирования представлены в табл. 1.

Таблица 1

Параметры для оценки химических и физико-химических свойств компонентов
дисперсных систем (Х₁-Х₈) и значения изучаемой характеристики (Y)

Таблица 2. Результаты дополнительного эксперимента для проверки работоспособности модели

Изучение парной корреляции переменных позволяет сделать вывод об отсутствии формализованной зависимости между ними. Только в трех парных корреляциях (Y=f(X₂), Y=f(X₃) и Y=f(X₄)) можно говорить о формализированном влиянии переменной на выходную функцию (коэффициент корреляции равен 0,9354).

Обработка данных, представленных в табл. 1, методом многоуровневого моделирования (путем составления системы нормальных уравнений и решения последней методом Гаусса) приводит к получению следующей модели:

Значение коэффициента ММУМ 0,9474. Проверка работоспособности модели для предсказания характеристики дубящих дисперсных систем была осуществлена путем решения линейного уравнения (подстановки данных Х1...Х8 из табл. 2) и сравнения расчетных и экспериментальных значений Y (табл. 3).

Расчетное значение Y, абсолютная (ε, %) и относительная (ε₁, %) ошибка расчетного значения

Данные табл. 2 свидетельствуют о незначительной абсолютной ошибке расчетных значений, при этом значение относительной ошибки увеличивается с уменьшением величины изучаемой характеристики. Для оценки значений относительной ошибки в диапазоне полученных значений Y по данным табл. 1 и табл. 2 методом многоуровневого моделирования была получена следующая модель: 

Значение коэффициента ММУМ 0,9543. График, иллюстрирующий изменение значения относительной ошибки (ε₁, %) при изменении значения Y (%) представлен на рис. 1.

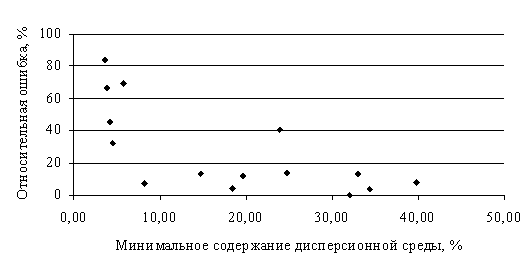
Рис. 1. Изменение значения относительной ошибки (ε₁, %) при изменении значения Y (%)

Из рисунка видно, что модель, полученная методом многоуровневого моделирования, достаточно точно описывает изучаемую характеристику в диапазоне изменения значения Y от 10 до 40 % и может быть использована для прогнозирования данной характеристики дисперсной системы. Увеличение относительной ошибки в интервале изучаемой характеристики менее 10 % может свидетельствовать об изменении характера структурных образований в исследуемых системах.

Для прогнозирования значений изучаемой характеристики в диапазоне менее 10 % необходимо разработать модель, основанную на соответствующих базовых параметрах.

СПИСОК ЛИТЕРАТУРЫ

1. Грачев Ю.П., Плаксин Ю.М. Математические методы планирования эксперимента.- М.: ДеЛи принт, 2005.- 296 с.

2. Танганов Б.Б. Взаимодействия в растворах электролитов: моделирование сольватационных процессов, равновесий в растворах полиэлектролитов и математическое прогнозирование свойств химических систем: Монография.- М.:Изд-во РАЕ, 2009.- 140с.

3. http://www.pereplet.ru/obrazovanie/stsoros/566.htm/