Формы связей между парциальными структурами в механических колебательных системах в существенной степени определяют возможности динамических состояний взаимодействующих элементов, что нашло отражение во многих известных работах, относящихся к физике, молекулярной механике и теории колебаний [1–5]. Выбор обобщенных координат может оказать большое влияние на формы и содержание взаимодействий, что, в конечном итоге, приводит к формированию критериев связности, получивших значительное развитие в молекулярной механике [1, 3].
В меньшей степени внимание уделяется взаимодействиям элементов механических колебательных систем, отражающих динамические свойства технических систем. В работах [6 ÷ 9] последних лет получили развитие некоторые концептуальные представления о возможностях расширения типового набора элементарных звеньев механических колебательных систем, что, в частности, нашло приложения в теории виброзащитных систем, имеющих в своем составе рычажные механизмы и устройства для преобразования движения [8, 9]. Реализация расширенного набора возникающих форм взаимодействия приводит к необходимости изучения форм связности парциальных систем, что определяется соотношениями различных видов движений отдельных элементов системы, например, вращательных и поступательных движений парциальных структур [10, 11]. Основное внимание при этом имеют критерии связности, при определении которых предполагается симметричность взаимодействий и однородность структур парциальных систем (по размерности взаимодействий).
Вместе с тем, существуют различные разновидности механических колебательных систем, в которых парциальные системы имеют движения различных видов, то есть взаимодействия происходят между твердыми телами, совершающими поступательное и вращательное движения.
Некоторые вопросы динамических взаимодействий в такого рода системах рассмотрены в работах [12, 13], однако особенности проявления рычажных связей и их влияние на свойства механических колебательных систем требуют более детализированного изучения.
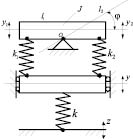
Рис. 1. Расчетная схема системы комбинированного типа (поступательное движение – по координате у; вращательное движение – относительно неподвижной
точки О)
В предлагаемой статье развиваются подходы, позволяющие учитывать динамические связи, возникающие в механических колебательных системах при различных видах парциальных движений, в частности, при наличии вращений, что приводит к появлению рычажных связей и соответствующих динамических особенностей. Динамические свойства систем рассматриваются в постановках задач линейной теории виброзащитных систем [6 ÷ 9].
I. Общие положения. Особенности подхода. Рассматривается механическая колебательная система (рис. 1), в которой массоинерционные элементы могут совершать вращательные и поступательные движения. Система имеет две степени свободы движений, которые могут описываться несколькими системами обобщенных координат. Отметим, что при оценке динамических свойств систем необходимо обращать внимание на однородность координат, что связано с вопросами совпадения размерности реакций связей. Между парциальными системами.
Если воспользоваться известной методикой построения математических моделей [6, 7], то уравнения движения при кинематическом возмущении z можно получить, предварительно определив выражения для кинетической и потенциальной энергий:
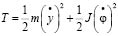; (1)
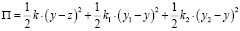; (2)
Введем ряд соотношений:
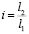– передаточное отношение при вращательном движении твердого тела;
; 
; 
.
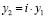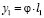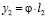Отметим, что у1 и у2 имеют различные направления движения. Выражение (2) можно записать в виде:
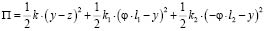. (3)
Проведем ряд вспомогательных преобразований, обычных при использовании формализма Лагранжа [9]. В координатах у и φ система уравнений движения для расчетной схемы на рис. 1 примет вид:
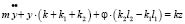; (4)
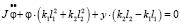. (5)
Структурная схема исходной системы
(с учетом преобразования Лапласа [6]) в координатах у, φ в соответствии с (4), (5) может быть представлена, как показано
на рис. 2.
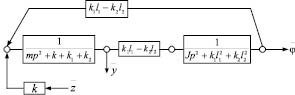
Рис. 2. Структурная схема исходной системы (рис. 1) в координатах y и φ
Структурная схема на рис. 2 может быть преобразована, как показано на рис. 3а, б, в и иметь несколько форм отобра-
жения.
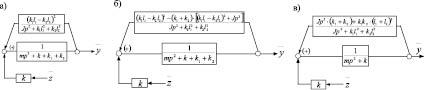
Рис. 3. Преобразование исходной структурной схемы:
а – исключение координаты φ; б – приведение к парциальной системе mp2 + k – положительная обратная связь; в – приведение системы к виду с отрицательной обратной связью
Передаточные функции системы могут быть найдены из структурных схем. Вместе с тем, такие же результаты можно непосредственно получить из уравнений (4), (5) после преобразований Лапласа:
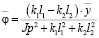; (6)
Используем (6) для исключения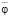 
:
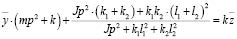. (7)
Если полагать, что парциальная система (по координате у) имеет вид
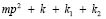, то уравнение (7) преобразуется:
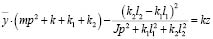. (8)
Таким образом, исходная система
(рис. 1) может быть приведена путем исключения координаты вращательного движения φ к системе с одной степенью свободы, в которой массоинерционный элемент m совершает поступательное прямолинейное движение.
В приложении к задачам виброзащиты можно массоинерционный элемент m рассматривать как объект защиты. В этом случае в структуре виброзащитной системы образуется некоторое устройство для преобразования движения, имеющее вид рычага второго рода [4]. Такой рычаг обладает массоинерционными свойствами (имеет момент инерции J относительно точки О (рис. 1).
В данном случае исходная система (рис. 1) может быть рассмотрена как система с одной степенью свободы. При этом, как показано на рис. 4 а, б, в системе появляется дополнительный элемент, который отличается от известных типовых элементов (в данном случае пружин с жесткостями k, k1, k2).
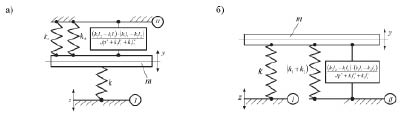
Рис. 4. Расчетная схема комбинированной системы, приведенная к системе, совершающей поступательное движение по координате у: а – опорные поверхности разнесены по вертикали;
б – опорные поверхности I и II разделены: возмущение z – по опорной поверхности I
Расчетная схема на рис. 4а, б предполагает использование опорных поверхностей I и II. Вводимое в схему на рис. 4 устройство для преобразования движения характеризуется приведенной динамической жесткостью, которая записана с использованием комплексной переменной p (p = jω [6]). При p = 0, то есть при отсутствии динамического возмущения со стороны основания
(z = 0) динамическая жесткость устройства для преобразования движения трансформируется в жесткость сложной пружины, имеющей в своем составе рычаг второго рода.
Из анализа расчетной схемы на рис. 4а, б следует также, что исходная система (рис. 1) преобразуется в эквивалентную в динамическом отношении систему, но с другим набором составных элементов. Координата φ исключается, но взаимодействия, привносимые вращательным движением по координате φ, остаются и отражаются квазипружиной (или компактом), имеющей приведенную жесткость:
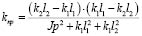. (9)
Квзипружина обладает тем свойством, что при определенных соотношениях параметров приведенная жесткость может стать отрицательной. В физическом смысле это означает изменение направления упругой силы, развиваемой квазипружиной. Такой же эффект может быть получен при изменении частоты внешнего воздействия, так как знаменатель (9) определяется выражением:
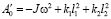, (9′)
которое при увеличении p (p = jω) также приобретает отрицательное значение.
Отметим, что в структурных преобразованиях квазипружина ведет себя как обыкновенный упругий элемент. Ряд вопросов, связанных с упомянутыми особенностями свойств рассмотрен в работах [14, 15].
II. Особенности преобразования систем. Из расчетной схемы на рис. 4 можно определить ряд характеристик.
Если между парциальными системами исходной системы на рис. 1 связность определяется звеном с передаточной функцией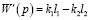 
, то связь между парциальными системами в координатах у, φ становится нулевой при выполнении условия 
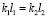. В этом случае при внешнем возмущении z система будет совершать движение как объект массой m, имея одну степень свободы. Парциальная частота системы совпадает с частотой собственных колебаний приведенной системы:
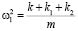. (10)
При этом величина момента инерции твердого тела J не имеет значения.
II. 1. Если <<elisl20.wmf>>, то интерес представляет случай, когда J = 0. В этом случае приведенная жесткость системы, формируемая с участием парциальной системы вращательного типа определится:
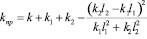. (11)
или
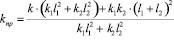. (11′)
При J = 0 в системе возможно появление рычажного механизма второго рода, который не только формирует для объекта массой m приведенную жесткость, но и создает вполне определенную структуру связей в пространстве (в геометрическом смысле). Приведенная схема системы (рис. 4) в этом случае может интерпретироваться в соответствии с рис. 5, где
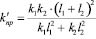. (12)
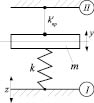
Рис. 5. Приведенная исходная расчетная схема при J = 0
Используем понятие передаточного отношения рычага:
.
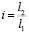Знак передаточного отношения, то есть особенности рычажного механизма учтены при выводе уравнений движения (в общем случае передаточное отношение рычага второго рода имеет знак минус):
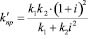. (13)
Если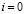 
, то 
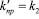. При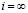 
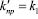, что совпадает с физическими представлениями о свойствах механической системы с рычажными связями.
II. 2. Рычаг второго рода с неподвижной точкой вращения (т. О) создает пространственную структуру расположения элементов механической колебательной системы. Если рычаг имеет нулевые массоинерционные характеристики, то дополнительно к основной пружине с жесткостью k он создает параллельную упругую связь, определяемую выражением (13).
Эта связь представляет собой упругое соединение объекта с массой m с опорной поверхностью II. В этом случае частота собственных колебаний определится как в системе с одной степенью свободы:
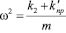. (14)
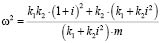. (14′)
Отметим, что передаточное отношение i может выступать в качестве настроечного параметра при решении различных задач, связанных с оценкой и контролем динамического состояния механических колебательных систем, в частности, виброзащитных [6, 8].
II. 3. Если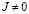 
, то есть вращательное звено обладает достаточно значимым моментом инерции, то приведенная жесткость квазипружины в отличие от выражения (13), будет зависеть от p. В этом случае приведенная жесткость квазипружины может быть названа динамической:
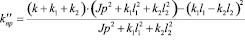, (15)
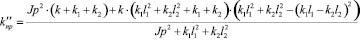. (15′)
Выражение (15′) дает представление о сложном характере связей, формирующихся при массивном рычаге в структуре объекта виброзащитной системы в том случае, когда объект совершает поступательное (прямолинейное) движение. Выражение (15′) можно также представить в виде:
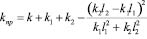. (16)
II. 4. С учетом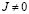 
исходная система становится системой с двумя степенями свободы, в которой парциальные системы имеют различные движения; одна система (координата у) реализует поступательный вид движения, другая (с координатой φ) – вращательное движение. Парциальные частоты системы могут быть определены из характеристического частотного уравне-
ния:
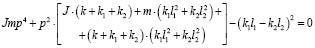. (17)
Частоты собственных колебаний в данном случае могут быть определены в виде:
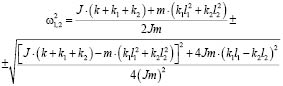. (18)
Запишем, что парциальные частоты определяются:
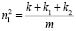. (19)
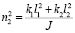. (20)
В свою очередь:
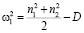; (21)
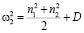. (22)
где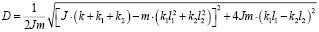 
. (23)
Таким образом, механическая колебательная система (рис. 1), имеющая две парциальные системы, состояние которых определяется координатами у и φ, может быть преобразована и приведена к более простой системе, характеризуемой координатой поступательного движения у. При этом «упрощении» в структуре системы становится необходимым введение элемента нового типа – он может быть назван квазипружиной и иметь соответствующую приведенную жесткость. В общем случае приведенная жесткость зависит от частоты внешнего воздействия и может быть названа динамической.
В работах [12 ÷ 18] квазипружина упомянутого вида получила название обобщенной пружины. Оба названия отражают одну и ту же физическую сущность, но их понятийные поля могут быть в различных контекстах использоваться по-разному. Важным обстоятельством является то, что при J = 0 в системе с одной степенью свободы становится возможным обосновать появление рычажных связей. Они реализуются в данном случае рычажным механизмом второго рода. Такие связи в механических колебательных системах привносят новые свойства.
III. Исключение координаты у. Используем структурную схему на рис. 2 и систему уравнений дви-
жения:
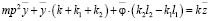; (24)
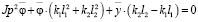. (25)
Из (24) следует, что:
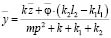. (26)
После подстановки (26) в (25) получим:
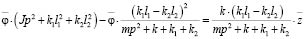. (27)
На рис. 6б приведена структурная схема исходной системы (рис. 1) при исключении координаты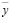 
. На рис. 6а приведена соответствующая расчетная схема в символической форме как механической системе с одной степенью свободы, определяемой координатой 
.
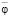Если рассмотреть расчетную схему парциальной системы с соответствующим вращательным движением, то она принимает вид, как показано на рис. 7.
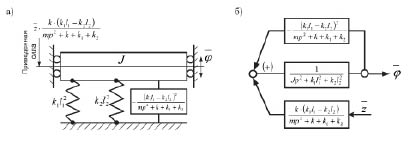
Рис. 6. Структурная (а) и расчетная (б) схемы при исключении координаты у
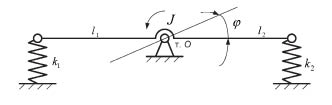
Рис. 7. Расчетная схема парциальной системы вращательного движения
Используя схему на рис.7, можно найти парциальную частоту:
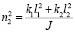. (28)
Это будут угловые колебания. Возвращаясь к расчетной схеме на рис. 6а, найдем, что приведенная жесткость квазипружины определяется формулой:
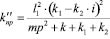. (29)
Выражение (29) соответствует крутильной динамической жесткости во вращательном движении с координатой φ.
Если исходную систему (рис. 1) привести к системе с одной степенью свободы (что можно сделать при исключении координаты у), то выражение (29) можно представить в детализированном, полагая, что:
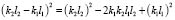. (29′)
Для того чтобы войти в формат расчетной схемы, отражающей особенности движения твердого тела относительно точки О, вернемся к уравнению (27). Сделаем ряд преобразований над 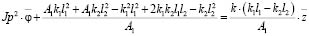(27):
(27′)
Тогда (27′) можно записать следующим образом:
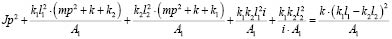. (27)
В этом случае расчетная схема (рис. 1) при исключении переменной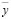 
примет вид как показано на рис. 8.
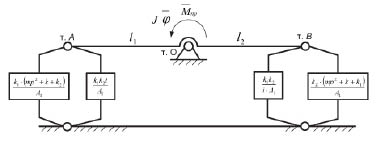
Рис. 8. Расчетная схема эквивалентной системы с одной степенью свободы с объектом, состояние которого описывается координатой φ (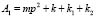
)
Отметим, что на рис. 8 принятые обозначения тт. А и В локализуют условия присоединения типовых элементов и квазипружин к объекту, совершающему вращательно-колебательное движение по координате φ. Приведенный момент сил, прикладываемый к объекту с моментом инерции J , формируется кинематическим возмущением z:
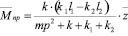. (30)
Что касается элементов структуры на рис.8 с использованием А1 , то они являются квазипружинами, жесткости которых во вращательном движении составляют:
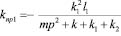; (31)
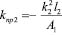; (32)
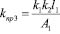; (33)
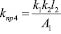. (34)
Таким образом, комбинированная система (рис. 1) приводится к рычажному механизму, в котором рычаг обладает моментом инерции J. При этом кинематическое возмущение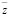 
преобразуется к приведенному моменту сил (рис. 8).
Если принять, что m = 0, то:
; 
; 
; 
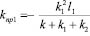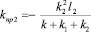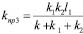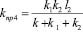, (35)
что позволяет привести упругие элементы к точкам А и В, что дает следующие результаты:
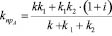; (36)
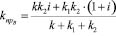. (37)
Таким образом, рассмотрение особенностей формирования рычажных связей показывает, что динамические свойства механических колебательных систем существенно зависит от особенностей парциальных систем, составляющих основу системы. Если парциальные системы неоднородны, то есть могут совершать и поступательные и вращательные движения, то большое значение приобретают рычажные связи. Можно предположить, что рычажные связи в колебательных системах могут принимать различные формы, что зависит от выбора обобщенных координат.
IV. Свойства системы с рычажными связями первого рода. Расчетная схема с двумя степенями свободы состоит из двух твердых тел и упругих связей. Твердое тело может двигаться поступательно, а второе – вращаться вокруг неподвижной точки, как показано на рис.9.
Система опирается на основание, закон движения которого известен (z(t) – гармоническое колебание).
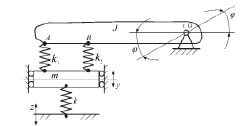
Рис.9. Расчетная схема системы с двумя твердыми телами, совершающими
вращательно-качательное (φ) и поступательное (у) движения
Твердые тела совершают малые движения. Принимается, что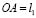 
, 
; 
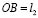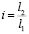– передаточное отношение рычажных связей.
Запишем выражения для кинетической и потенциальной энергий:
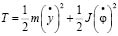; (38)
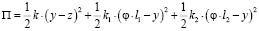. (39)
Уравнения движения в координатах у и φ имеют вид:
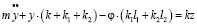; (40)
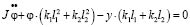. (41)
Из (41) найдем, что:
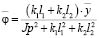. (42)
Подставив (42) в (40), получим (в изображениях по Лапласу) при исключении координаты φ:
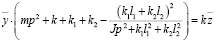. (43)
Структурная схема системы (рис. 9) с её формами преобразования приведена на рис.10а, б. При этом, схема на рис.10а соответствует двум степеням свободы движения, а на рис.10б – схема преобразована и координата φ исключена. Внешнее воздействие представляет собой движение основания пружины с жесткостью k, определяемое через z. Также, как и в исходной системе на рис.1, можно выделить появление квазипружины с приведенной жесткостью:
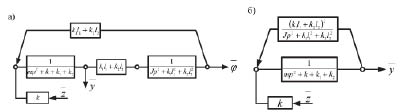
Рис. 10. Структурная схема (а), соответствующая системе на рис.8; б – структурная схема с исключением координаты φ
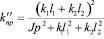. (44)
Выражение (44) отличается от аналогичного выражения (9) тем, что в числителе стоит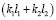 
, а не 
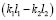, что соответствует изменению вида рычажной связи.
Преобразуем (44), вводя передаточное отношение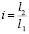 
и получим, что:
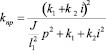. (45)
На рис. 11 приведена расчетная схема в виде системы с одной степенью свободы и объектом защиты m (координата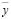 
).
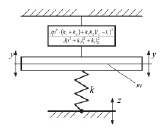
Рис. 11. Расчетная схема системы с рычажной связью первого рода
Если принять, что J = 0, то:
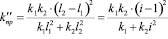. (46)
Если взять за основу расчетную схему на рис.4а, но использовать рычажную связь первого рода, то расчетная схема примет вид, как показано на рис. 12.
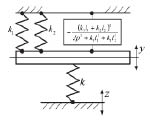
Рис. 12. Расчетная схема системы с рычажным звеном первого рода
Введение рычажных связей (через твердое тело с моментом инерции J) другого типа изменяет значения приведенных жесткостей квазипружин. В связи с этим будут изменяться и свойства механической колебательной системы в целом. Что касается рассматриваемого на рис. 12 случая, то в нем предполагается постановка задачи вибрационной защиты с объектом в виде массоинерционного элемента структуры (m), тогда как рычажная связь используется для настроечных целей.
Заключение
Приведенные материалы свидетельствуют о том, что между вращательными и поступательными движениями при реализации структурных подходов выявляется адекватность представлений о правилах преобразований. Главное заключается в том, что рычажные связи появляются в результате абстрагирования от некоторых особенностей вращательного движения. Оно характеризуется тем, что связи между типовыми элементами в системе разнесены в пространстве, что делает обоснованным введение и рычажных связей и рычажных механизмов.
Показано, что разделение рычажных связей вполне объяснимо, если принять во внимание характер локализации мест закрепления связей относительно неподвижной точки рычага. Если связи многочисленные и располагаются с разных сторон точки вращения рычага. То структура передаточных отношений должна корректироваться в связи с выбором точек крепления элементов по отношению к точке вращения рычага.
В данной работе парциальные системы выбраны таким образом, что вращательное движение и поступательное физически разделены и в качестве межпарциальных связей выступают упругие элементы k1 и k2 . Однако существуют системы, в которых твердое тело объединяет отдельные виды движений в одно (это плоское движение). В этом случае парциальные связи будут носить другой характер (часто их называют инерционными [6, 9]). Такие системы также могут быть приведены к эквивалентному виду цепной системы, что, в частности, рассматривалось в работах [16 ÷ 18].
Работа выполнена при поддержке Федеральной целевой программы «Научные и педагогические кадры инновационной России (2012-2013)» по теме «Мехатроника виброзащитных колебательных систем» (№ 14.132. 21. 1362).