В ряду наиболее важных транспортных свойств как электропроводность, вязкость, диффузия и теплопроводность растворов электролитов, одним из самых интересных как с прикладной, так и фундаментальной точки зрения является теплопроводность. Теплопроводность водных растворов электролитов, несмотря на попытки многих ученых, является неизученной областью исследования. В литературных источниках встречаются значения теплопроводности только нескольких наиболее используемых электролитов, изученных в узкой области изменения температур и концентраций.
Цель исследования. Реальных попыток создать единую теоретическую модель расчета коэффициента теплопроводности растворов электролитов невозможно вспомнить, что мы и стараемся воплотить в наших работах [1].
При решении проблемы теплопроводности водных растворов смесей электролитов в рамках разработанной теоретической модели состояний ионов в растворах электролитов, основанной на концепции ионной плазмы, введены мольные доли ионных составляющих при оценке приведенных масс сольватированных и несольватированных ионов.
Материалы и методы исследования
На растворах электролитов была апробирована теоретическая модель оценки теплопроводности водных растворов индивидуальных электролитов в широком диапазоне изменения концентраций и температур. Данная модель основывается на ион-дипольном взаимодействии, учитывающемся в уравнениях для оценки сольватных чисел большинства ионов с известными радиусами, масс и радиусов сольватированных ионов. Кроме того решена проблема подвижности ионов и молекул электролитов, основанная на использовании приведенных масс и размеров гидратированных частиц, параметра Дебая и др. [2-10].
На данном этапе представляет интерес изучение возможности использования разработанной теоретической модели для оценки теплопроводности смесей электролитов.
В общем виде уравнение для определения коэффициента теплопроводности смешанных электролитов имеет вид:
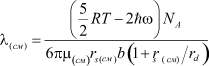 ,
,
где R – газовая постоянная; T – температура, К; 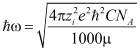 – энергия колебательного процесса «ассоциация – диссоциация»; zie – элементарный заряд;
– энергия колебательного процесса «ассоциация – диссоциация»; zie – элементарный заряд; 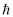 – постоянная Планка; C – концентрация раствора, моль/л; NA – постоянная Авогадро;
– постоянная Планка; C – концентрация раствора, моль/л; NA – постоянная Авогадро; 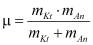 – приведенная масса несольватированных ионов;
– приведенная масса несольватированных ионов; 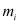 – масса несольватированного иона;
– масса несольватированного иона; 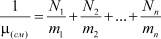 – приведенная масса несольватированных ионов в смеси;
– приведенная масса несольватированных ионов в смеси; 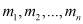 – массы несольватированных ионов в смеси;
– массы несольватированных ионов в смеси; 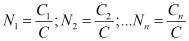 – мольные доли ионов;
– мольные доли ионов; 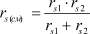 – приведенный радиус сольватированных ионов;
– приведенный радиус сольватированных ионов; 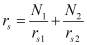 – радиус сольватированных ионов смеси электролитов;
– радиус сольватированных ионов смеси электролитов; 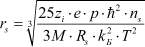 – радиус сольватированных ионов электролита; p – дипольный момент молекулы растворителя;
– радиус сольватированных ионов электролита; p – дипольный момент молекулы растворителя; 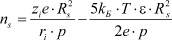 – сольватное число иона; Rs – радиус молекулы растворителя; ri – радиус иона; kБ – постоянная Больцмана; ε – диэлектрическая постоянная; M – молярная масса растворителя;
– сольватное число иона; Rs – радиус молекулы растворителя; ri – радиус иона; kБ – постоянная Больцмана; ε – диэлектрическая постоянная; M – молярная масса растворителя; 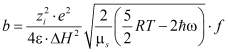 – подвижность иона;
– подвижность иона; 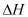 – энергия водородной связи растворителя;
– энергия водородной связи растворителя; 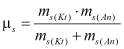 – приведенная масса сольватированных ионов;
– приведенная масса сольватированных ионов; 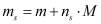 – масса сольватированного иона;
– масса сольватированного иона; 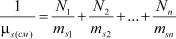 – приведенная масса сольватированных ионов в смеси;
– приведенная масса сольватированных ионов в смеси; 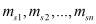 – массы сольватированных ионов в смеси;
– массы сольватированных ионов в смеси; 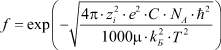 – функция максвелловского распределения по скоростям движения ионов;
– функция максвелловского распределения по скоростям движения ионов; 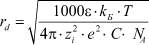 – дебаевский радиус экранирования.
– дебаевский радиус экранирования.
Результаты исследования и их обсуждение
Были изучены разнообразные пары смесей, которые содержали симметричные и несимметричные электролиты. В табл. 1 представлены полученные расчетные данные по теплопроводности водных растворов некоторых смесей I-I электролитов.
Таблица 1
Значения коэффициента теплопроводности водных растворов смесей I-I электролитов
|
Т, К |
С1, моль/л |
С2, моль/л |
|
||
|
KCl и KBr |
NaNO3 и KBr |
NH4Cl и KBr |
|||
|
288 |
2,5 |
0,5 |
533 |
562 |
568 |
|
2,0 |
1,0 |
532 |
551 |
553 |
|
|
1,5 |
1,5 |
525 |
531 |
527 |
|
|
1,0 |
2,0 |
514 |
507 |
494 |
|
|
0,5 |
2,5 |
498 |
490 |
473 |
|
|
293 |
2,5 |
0,5 |
536 |
565 |
570 |
|
2,0 |
1,0 |
536 |
554 |
556 |
|
|
1,5 |
1,5 |
529 |
535 |
530 |
|
|
1,0 |
2,0 |
518 |
510 |
498 |
|
|
0,5 |
2,5 |
502 |
493 |
477 |
|
|
298 |
2,5 |
0,5 |
539 |
568 |
573 |
|
2,0 |
1,0 |
539 |
557 |
559 |
|
|
1,5 |
1,5 |
533 |
538 |
534 |
|
|
1,0 |
2,0 |
522 |
514 |
501 |
|
|
0,5 |
2,5 |
506 |
497 |
481 |
|
|
303 |
2,5 |
0,5 |
543 |
571 |
575 |
|
2,0 |
1,0 |
543 |
560 |
562 |
|
|
1,5 |
1,5 |
536 |
541 |
537 |
|
|
1,0 |
2,0 |
526 |
518 |
505 |
|
|
0,5 |
2,5 |
510 |
501 |
486 |
|
|
308 |
2,5 |
0,5 |
546 |
574 |
578 |
|
2,0 |
1,0 |
546 |
563 |
565 |
|
|
1,5 |
1,5 |
540 |
545 |
541 |
|
|
1,0 |
2,0 |
530 |
521 |
509 |
|
|
0,5 |
2,5 |
514 |
505 |
490 |
|
|
313 |
2,5 |
0,5 |
549 |
577 |
581 |
|
2,0 |
1,0 |
549 |
566 |
567 |
|
|
1,5 |
1,5 |
543 |
547 |
544 |
|
|
1,0 |
2,0 |
533 |
524 |
513 |
|
|
0,5 |
2,5 |
518 |
508 |
495 |
|
|
308 |
2,5 |
0,5 |
553 |
580 |
584 |
|
2,0 |
1,0 |
553 |
569 |
571 |
|
|
1,5 |
1,5 |
548 |
551 |
548 |
|
|
1,0 |
2,0 |
538 |
528 |
518 |
|
|
0,5 |
2,5 |
522 |
513 |
500 |
|
|
323 |
2,5 |
0,5 |
557 |
583 |
587 |
|
2,0 |
1,0 |
557 |
572 |
575 |
|
|
1,5 |
1,5 |
551 |
555 |
552 |
|
|
1,0 |
2,0 |
542 |
532 |
522 |
|
|
0,5 |
2,5 |
527 |
517 |
505 |
|
Также были изучены смеси из симметричных и несимметричных электролитов, содержащих многозарядные ионы. В табл. 2 представлены расчетные значения теплопроводности водных растворов таких смесей.
Таблица 2
Значения коэффициента теплопроводности водных растворов смесей II-I(III-I) и I-I электролитов
|
Т, К |
С1, моль/л |
С2, моль/л |
|
||
|
AlCl3 и NaNO3 |
BaCl2 и KCl |
BaCl2 и KBr |
|||
|
288 |
2,5 |
0,5 |
583 |
505 |
564 |
|
2,0 |
1,0 |
560 |
509 |
551 |
|
|
1,5 |
1,5 |
547 |
519 |
547 |
|
|
1,0 |
2,0 |
529 |
522 |
538 |
|
|
0,5 |
2,5 |
507 |
516 |
524 |
|
|
293 |
2,5 |
0,5 |
585 |
506 |
565 |
|
2,0 |
1,0 |
562 |
510 |
553 |
|
|
1,5 |
1,5 |
549 |
520 |
549 |
|
|
1,0 |
2,0 |
532 |
522 |
540 |
|
|
0,5 |
2,5 |
511 |
517 |
526 |
|
|
298 |
2,5 |
0,5 |
586 |
507 |
567 |
|
2,0 |
1,0 |
563 |
511 |
555 |
|
|
1,5 |
1,5 |
551 |
521 |
551 |
|
|
1,0 |
2,0 |
535 |
523 |
542 |
|
|
0,5 |
2,5 |
515 |
518 |
528 |
|
|
303 |
2,5 |
0,5 |
587 |
509 |
569 |
|
2,0 |
1,0 |
565 |
512 |
556 |
|
|
1,5 |
1,5 |
554 |
522 |
553 |
|
|
1,0 |
2,0 |
538 |
524 |
545 |
|
|
0,5 |
2,5 |
519 |
468 |
531 |
|
|
308 |
2,5 |
0,5 |
589 |
510 |
571 |
|
2,0 |
1,0 |
567 |
513 |
558 |
|
|
1,5 |
1,5 |
557 |
523 |
555 |
|
|
1,0 |
2,0 |
542 |
525 |
547 |
|
|
0,5 |
2,5 |
524 |
520 |
534 |
|
|
313 |
2,5 |
0,5 |
590 |
511 |
572 |
|
2,0 |
1,0 |
569 |
514 |
560 |
|
|
1,5 |
1,5 |
559 |
523 |
556 |
|
|
1,0 |
2,0 |
546 |
526 |
549 |
|
|
0,5 |
2,5 |
529 |
520 |
536 |
|
|
308 |
2,5 |
0,5 |
592 |
513 |
574 |
|
2,0 |
1,0 |
572 |
516 |
562 |
|
|
1,5 |
1,5 |
563 |
525 |
559 |
|
|
1,0 |
2,0 |
551 |
527 |
552 |
|
|
0,5 |
2,5 |
535 |
522 |
539 |
|
|
323 |
2,5 |
0,5 |
594 |
514 |
576 |
|
2,0 |
1,0 |
575 |
517 |
564 |
|
|
1,5 |
1,5 |
567 |
526 |
561 |
|
|
1,0 |
2,0 |
556 |
529 |
554 |
|
|
0,5 |
2,5 |
542 |
523 |
542 |
|
Заключение
Полученные результаты свидетельствуют о том, что теоретическая расчетная модель может применяться для оценки значений коэффициента теплопроводности смесей электролитов. Данная модель может применяться для двухкомпонентных смесей симметричных и несимметричных электролитов.
Предлагаемая модель расчета теплопроводности водных растворов смесей электролитов может быть апробирована на трехкомпонентных водных растворах электролитов. А в дальнейшем разработанная модель позволит проводить теоретические оценки температурной и концентрационной зависимости теплопроводности электролитов в смешанных растворителях. Поскольку смешанные растворители имеют ряд неоспоримых преимуществ перед индивидуальными растворителями, одним из которых является высокая растворяющая способность в отношении плохо или вовсе нерастворимых веществ в индивидуальных растворителях.


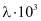 , [Вт/(м×К)]
, [Вт/(м×К)]
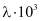 , [Вт/(м×К)]
, [Вт/(м×К)]