Плоская структура пространства – времени при относительно низких энергиях может быть нарушена пространственно - временной пеной квантовых флуктуаций. Для её обнаружения в 2011 – 2012 годах на оборудовании спутника INTEGRAL и космической обсерватории IKAROS были выполнены уникальные измерения параметра нарушения лоренц – инвариантности ![]() и поляризационных параметров излучения в жестком ренгеновском, мягком гамма – диапазонах 50 – 800 кэв. На параметр нарушения лоренц – инвариантности (LV) были наложены жёсткие ограничения
и поляризационных параметров излучения в жестком ренгеновском, мягком гамма – диапазонах 50 – 800 кэв. На параметр нарушения лоренц – инвариантности (LV) были наложены жёсткие ограничения ![]() [1], тогда как средняя линейная поляризация излучения
[1], тогда как средняя линейная поляризация излучения ![]() [2]. Обе группы использовали простейшую формулу для эффекта LV [3] (далее используется естественная система единиц
[2]. Обе группы использовали простейшую формулу для эффекта LV [3] (далее используется естественная система единиц ![]() ):
):
![]() , (2)
, (2)
где ![]() Гэв – планковская энергетическая шкала,
Гэв – планковская энергетическая шкала, ![]() .
.
Из формулы (2) вытекает неравенство скоростей левых и правых фотонов. Поэтому, излучение становится поляризованным, что и зафиксировано в (1) на феноменологическом уровне. Эксперимент IBIS/SPI/INTEGRAL проводился в астрофизическом окне поляризованного рентгеновского излучения с энергией квантов света 250 <E<800 кэв [1]. Однако, этот эффект обнаружен не был. Напротив, в эксперименте GAP/IKARUS в диапазоне энергий 50 <E<300 кэв с помощью поляриметра GAP был обнаружен поток поляризованного излучения от послесвечений гамма – всплесков и оценена линейная поляризация этого излучения.
Рассмотрим максимально общий спектр электромагнитных волн, принимаемый от источника с учётом фрактальной материи. Теория калибровочно – инвариантного фрактального электромагнитного поля с источниками была построена в [4]. При высоких энергиях в физических полях может возникать нарушение Лоренц – инвариантности (LV) [3]. Построим теорию фрактального электромагнитного поля с LV.
Тензор калибровочно – инвариантного фрактального поля, обладающий свойствами причинности есть:
![]() (
(![]() ) (3)
) (3)
Здесь и ниже греческие индексы обозначают дробную фрактальную производную Риса и пробегают значения 0<α,β,γ<1. В (3) дробная производная Риса по каждой из координат ха определена как в [3].
Лагранжиан поля с нарушенной лоренц – инвариантностью имеет вид:
![]() (4)
(4)
здесь M – энергетическая шкала LV нарушения,
![]() -численный коэффициент(
-численный коэффициент(![]() ),
),
nc – нормированный единичный вектор
![]() ,
, ![]() .
.
![]() - дуальный тензор электромагнитного поля.
- дуальный тензор электромагнитного поля.
Варьируя действие с функцией Лагранжа (4) в калибровке Лоренца ![]() , получаем уравнения поля
, получаем уравнения поля
![]() (5)
(5)
Получим из (5) уравнения для плоской поляризованной электромагнитной волны, распространяющейся вдоль оси «z» трёхмерного пространства
![]() , (6)
, (6)
где вектор поляризации определён стандартно
![]() (7)
(7)
Дисперсионное соотношение для плоской свободной (![]() ) фрактальной электромагнитной волны с растущей высокоэнергетической модой (
) фрактальной электромагнитной волны с растущей высокоэнергетической модой (![]() ) получено в [4]:
) получено в [4]:
![]() (8)
(8)
Пользуясь (5), рассчитаем поправку к (8) методом последовательных приближений по параметру ![]() :
:
![]() (9)
(9)
Учтём, что измерения производятся в гравитационном поле стандартной модели Вселенной. Введём систему отсчёта с метрикой расширяющейся Вселенной, масштабным фактором:
![]() (10)
(10)
В этой метрике для механизма (2) частота волны примет вид [6]:
![]() (11)
(11)
![]() - масштабный фактор Вселенной в настоящий момент времени. Предположим, что источник, находящийся на расстоянии с красным смещением z =
- масштабный фактор Вселенной в настоящий момент времени. Предположим, что источник, находящийся на расстоянии с красным смещением z = ![]() ,
,
генерирует волну, содержащую как суперпозицию левой (LP) и правой (RP) поляризаций, так и циркулярную поляризацию (CPR). Вектор – потенциал поляризованной электромагнитной волны может быть представлен в виде, где волна записана как суперпозиция лево- и право - поляризованных волн [6]. Перепишем (11) через квантовую поправку к частоте ![]() , релятивистскую частоту волны в метрике (10) как
, релятивистскую частоту волны в метрике (10) как
![]() . (12)
. (12)
Теперь вектор – потенциал (14) можно переписать в функции от фазы смешивания поляризаций ![]() амплитуды
амплитуды ![]()
![]() (13)
(13)
Рассчитаем напряжённость электрического поля волны в унитарной калибровке:
![]() (14)
(14)
![]() (15)
(15)
Спектральная плотность принимаемого пакета плоских волн имеет вид n(P). Поляризационные параметры Стокса для этого пакета аналогично [6] с учётом нелинейных по параметру b смешивания поляризаций членов:
Ip = n(P)W2(![]() )= n(P)
)= n(P)![]() (16)
(16)
Q = n(P)![]() = n(P)
= n(P)![]() (17)
(17)
U = n(P)![]() = - n(P)
= - n(P)![]() (18)
(18)
V = n(P)![]() = n(P)
= n(P)![]() (19)
(19)
Построенные параметры образуют ортогональный поляризационный базис Стокса:
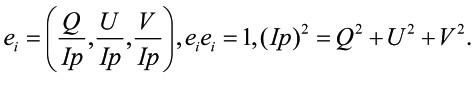 (20)
(20)
Приёмник излучения, принимая волну, усредняет её параметры X(E) по энергетическому спектру [7]. Моменты усреднения имеют вид:
![]() (21)
(21)
Введём безразмерную энергию ![]() , (E0 - начальная точка отсчёта энергии
, (E0 - начальная точка отсчёта энергии
в спектре). В рассматриваемом пакете плоских волн
![]() =
=![]() (22)
(22)
Средний квадрат мощности принимаемого волнового пакета
![]() (23)
(23)
Среднее значение линейной поляризации в рассматриваемой модели:
![]() (24)
(24)
Кривая L(b) изображена на Рис.1. В эксперименте GAP [2] получено ограничение на линейную поляризацию послесвечения гамма – всплеска GRB 110721A L>0.35, соответствующее значению -1.21<b<3.07 в формуле (26). По измерениям GAP, спектр энергии в поляриметре ![]() . Зафиксируем f(P)=
. Зафиксируем f(P)= ![]() /
/![]() . Тогда разность фаз примет в модели (2) есть:
. Тогда разность фаз примет в модели (2) есть:
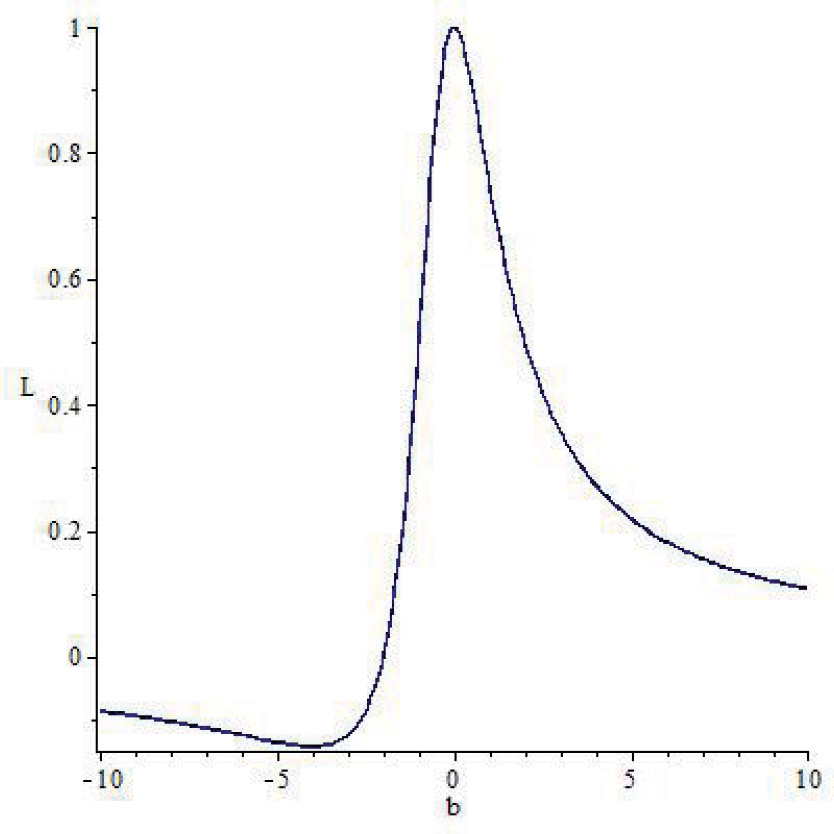
Рис. 1. Зависимость поляризации L излучения гамма- всплеска от параметра смешивания b.
![]() (25)
(25)
Рассчитаем, к примеру, ![]() Пользуясь (18), (19), имеем
Пользуясь (18), (19), имеем
![]() ( а=2). (26)
( а=2). (26)
Нормированные усреднённые поляризационные параметры есть:
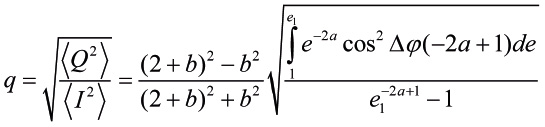 (27)
(27)
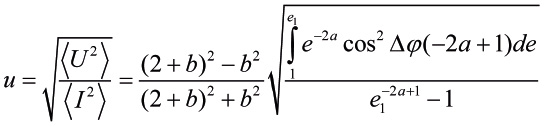 (28)
(28)
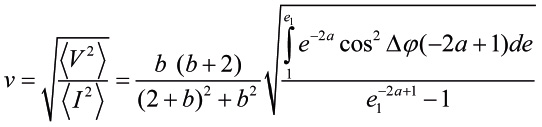 (29)
(29)
Оценим фазу ![]() . В используемой системе единиц
. В используемой системе единиц ![]()
![]() ~
~![]() /
/![]() ~
~ ![]() /
/![]() (30)
(30)
Нормируя в (26) энергию на Е0=300Кэв, введём безразмерную энергию e=Е/Е0. Тогда ![]() .
.
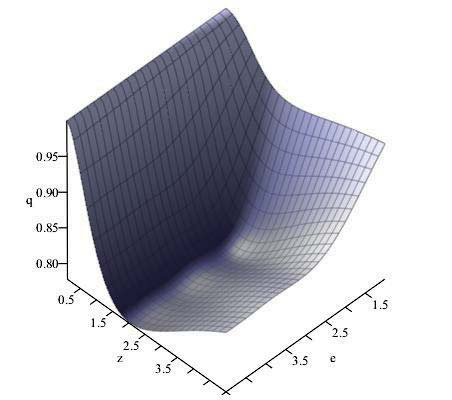
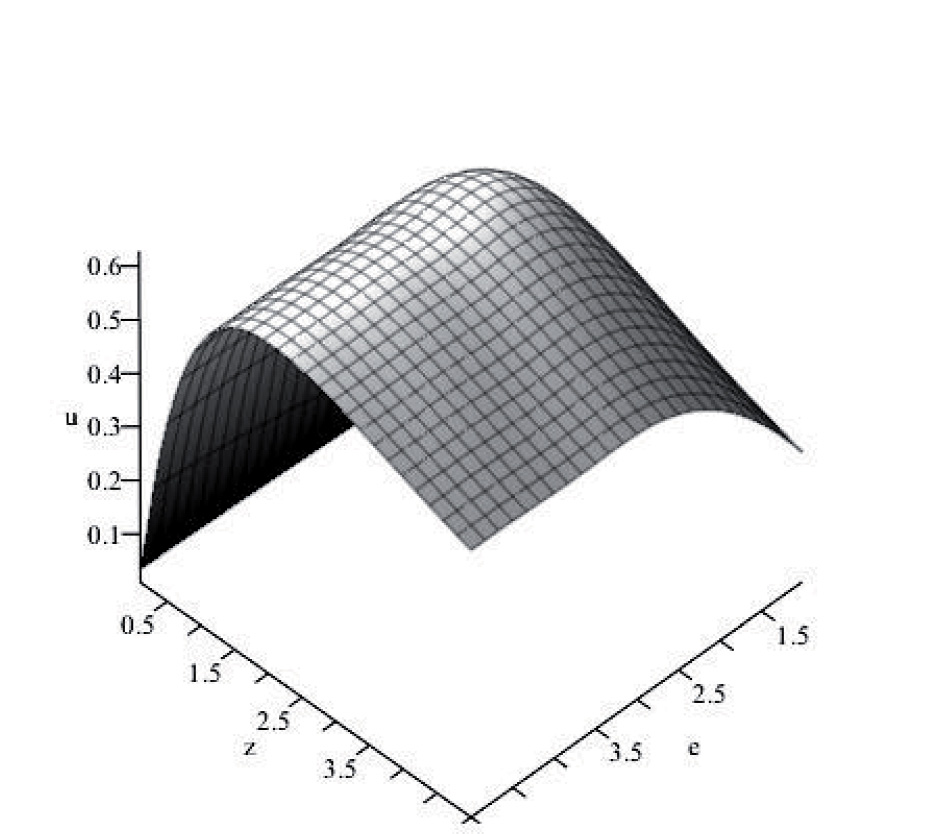
Из Рис.2 видно, что при энергии E0 и существующих сегодня оценках ![]() наблюдается осцилляционный минимум для поляризационного параметра q по красному смещению. Как следует из Рис.3., для параметра u расчет предсказывает появление поляризационного максимума по z .
наблюдается осцилляционный минимум для поляризационного параметра q по красному смещению. Как следует из Рис.3., для параметра u расчет предсказывает появление поляризационного максимума по z .
|
Рис.2. Осцилляционный минимум поляризационного параметра q по красному смещению z при b=0. |
Рис.3. Осцилляционный максимум поляризационного параметра u по красному смещению z при b=0. |
Из Рис.1 видно, что результаты экспериментов GAP/IKAROS и IBIS/INTEGRAL согласуются друг с другом при больших абсолютных значениях параметра смешивания b, малой поляризации излучения L.