Наиболее сложный режим работы гидростойки возникает вследствие динамической осадки кровли, во время которого происходит резкое повышение давления рабочей .жидкости. Это может привести к возникновению деформации или разрушению элементов гидростойки.
Для определения степени влияния данного режима работы на конструкцию гидростойки в работе Шеина Ю.Г. [1] предложен метод определения динамического коэффициента, который характеризует увеличение нагрузок на крепь и смещений ее податливых узлов. Одним из важнейших параметров, необходимых для вычисления динамического коэффициента, является относительное время действия импульса τ*:
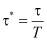 , (1)
, (1)
где τ – реальное время действия повышенной нагрузки, с; Т – период колебаний системы, с.
При динамической постановке задачи в уравнение равновесия рассматриваемой конструкции вводятся матрица масс элементов и матрица коэффициентов демпфирования, учитывающая силы вязкого сопротивления. При квазистатической постановке задачи конструкция рассчитывается в конкретный интересующий момент времени при статическом нагружении [1, 2].
Частоту собственных колебаний ω можно определить, выразив ее из формулы (1):
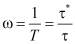 . (2)
. (2)
Для исследования давления рабочей жидкости р, раздвижности lр, внутреннего диаметра d1в, длины lц и толщины стенки S цилиндра на значения собственных частот цилиндра была разработана трехмерная конечно-элементная параметрическая модель гидростойки (рис. 1).
Наиболее важными параметрами, изменяющимися в процессе работы и не зависящими от конструкции гидростойки, являются давление рабочей жидкости и раздвижность.

Рис. 1. Параметрическая трехмерная модель для определения частот собственных колебаний
Для исследования влияния давления рабочей жидкости р на частоты собственных колебаний цилиндра принимались следующие значения давлений: 0, 10, 30, 50, 70,100 и 150 МПа. Расчеты проводились в два этапа. На первом определялись предварительные напряжения при заданном давлении и раздвижности, а на втором – значения частот и формы собственных колебаний с учетом этих напряжений. Результаты расчетов показали, что в данном диапазоне частот находится только две формы колебаний: поперечная (рис. 2, а) и осевая (рис. 2, б).
а 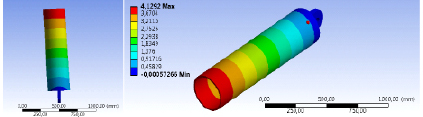 б
б
Рис. 2. Формы колебаний цилиндра гидростойки с изолиниями суммарных деформаций: а – поперечные колебания; б – осевые колебания
На рис. 3 (а, б) приведены зависимости частоты собственных колебаний от давления в поршневой полости. Проведенный регрессионный анализ показал, что данные зависимости близки к прямолинейным и выражаются уравнениями:
ωп = –0,0059·р + 524,81, (3)
ωо = –0,0025·р + 823,18 (4)
где ωп, ωо – частоты собственных поперечных и осевых колебаний, Гц; р – давление в поршневой полости, МПа.
а 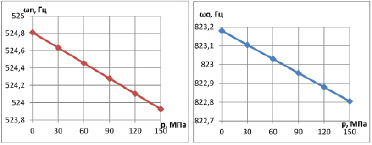 б
б
Рис. 3. Зависимость частоты собственных колебаний от давления рабочей жидкости: а – поперечные колебания; б – осевые колебания
Как видно из представленных зависимостей давление рабочей жидкости незначительно влияет на значения частот собственных колебаний цилиндра, т.к. при его изменении от 0 до 150 МПа наибольшая разница значений частот собственных поперечных колебаний составила 0,88 Гц, осевых – около 0,38 Гц. Поэтому при расчетах этим параметром можно пренебречь, а следовательно и раздвижностью, т. к. давление рабочей жидкости незначительно влияет на частоту собственных колебаний самой конструкции цилиндра.
Для оценки влияние формы конструкции цилиндра на значения частот собственных колебаний были выбраны следующие геометрические параметры: толщина стенки, внутренний диаметр и длина цилиндра. Расчеты проводились на трехмерной параметрической модели. Давление в поршневой полости равнялось 0 Па. Поиск частот собственных колебаний проводился в диапазоне от 0 до 1000 Гц.
Расчеты проводились в один этап, т.к. при нулевом давлении в поршневой полости нет необходимости определять предварительные напряжения. Определялись формы и значения частот собственных колебаний.
При исследовании влияния толщины стенки цилиндра на частоты собственных колебаний в расчетах принято S = 0,015, 0,020, 0,025, 0,030, 0,035, 0,040, 0,045 м. Остальные параметры модели оставались неизменными.
Результаты расчетов показали, что в данном диапазоне частот так же находится две формы колебаний. На рисунках 4а и 4б представлены зависимости частот собственных колебаний от толщины стенки цилиндра. Проведенный регрессионный анализ показал, что эти зависимости имеют форму параболы и их можно описать полиномами второй степени:
ωп = –31351·S2+ 1908,3·S + 497,74, (5)
ωо = 102878·S2– 14718·S + 1103,3. (6)
а 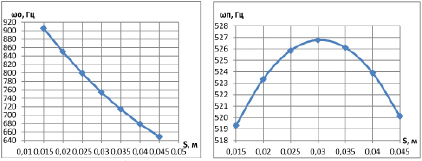 б
б
Рис. 4. Зависимость частоты собственных поперечных колебаний от толщины стенки цилиндра: а – поперечные колебания; б – осевые колебания
Анализ зависимостей (5, 6) показал, что толщина стенки цилиндра оказывает незначительное влияния на частоту собственных поперечных колебаний. При изменении толщины стенки в 3 раза (с 0,015 до 0,045 м) наибольшая разница составляет всего 2,5 %. При этом наибольшее значение ωп принимает при толщине стенки цилиндра S = 0,03 м и составляет 526,78 Гц. А на частоту собственных осевых колебаний толщина стенки цилиндра наоборот оказывает существенное влияние. При изменении толщины стенки так же в 3 раза частота собственных осевых колебаний снижается примерно на 28,3 % от максимального значения (с 905,68 до 649,32 Гц).
При исследовании влияния внутреннего диаметра на частоты собственных колебаний расчеты проводились при d1в = 0,18, 0,20, 0,22, 0,24, 0,25, 0,26, 0,28 м.
В данном диапазоне частот, как и в предыдущих случаях, находится только две формы колебаний: продольная и поперечная. На рисунках 5а и 5б представлены зависимости частоты собственных колебаний от внутреннего диаметра цилиндра. Проведенный регрессионный анализ показал, что зависимость частоты собственных поперечных колебаний близка к прямолинейной и ее можно выразить уравнением:
ωп = 1674,9·d1в + 184,65. (7)
Зависимость частоты собственных осевых колебаний можно описать полиномом второй степени:
ωо = –4494,7d1в2+ 1236,2d1в + 755,92. (8)
Значения коэффициентов детерминации составили, соответственно, 0,99 и 1, а остаточные дисперсии 43,23 и 0,109.
а 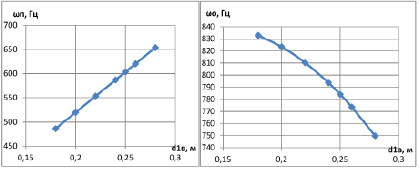 б
б
Рис. 5. Зависимость частоты собственных колебаний от внутреннего диаметра цилиндра: а – поперечные колебания; б – осевые колебания
Из графиков зависимостей частот собственных колебаний от внутреннего диаметра цилиндра (рис. 5) видно, что при увеличении внутреннего диаметра в 1,5 раза (с 0,18 до 0,28 м) частота собственных поперечных колебаний увеличивается примерно на 25 % (с 486,1 до 653,6 Гц) за счет увеличения поперечной жесткости цилиндра. И наоборот, частота собственных осевых колебаний уменьшается примерно на 10 % (с 832,8 до 749,7 Гц) за счет увеличения площади дна.
При исследовании влияния длины цилиндра на частоты собственных колебаний в расчетах принималось lц = 1,00, 1,15, 1,20, 1,30, 1,35, 1,45 и 1,50 м.
В этом диапазоне частот также имеем две формы колебаний: продольную и поперечную. Установлено, что зависимости можно описать полиномами третей степени:
ωп = –184,03·lц3+1190,8·lц2–2728·lц+2381,1; (9)
ωо = –116,44·lц3+763,49·lц2–1869,6·lц+2152,1. (10)
Анализ зависимостей (9 и 10) показал, что из всех рассмотренных параметров длина цилиндра оказывает наибольшее влияние на частоты собственных колебаний. С увеличением ее в 1,5 раза (с 1 м до 1,5 м), частота собственных поперечных колебаний уменьшается в 2 раза (с 659,87 Гц до 347,29 Гц), а частота собственных осевых колебаний в 1,4 раза (с 929,55 до 672,56 Гц).
Наибольшее влияние на частоту собственных колебаний цилиндра гидростойки оказывают его длина и внутренний диаметр. Частота собственных поперечных и осевых колебаний от длины цилиндра имеют гиперболическую зависимость. Частота собственных поперечных колебаний имеет линейную зависимость от внутреннего диаметра цилиндра, а частота собственных осевых колебаний – гиперболическую зависимость. Такими параметрами гидростойки, как давление рабочей жидкости, раздвижность и толщина стенки цилиндра, можно пренебречь при определении частоты собственных колебаний цилиндра в силу их незначительного влияния.

