Вопрос о самодействии в магнитостатике, судя по всему, до сих пор не закрыт. И это так, несмотря на то, что наконец удалось измерить так называемую силу самодействия, с которой незамкнутый участок тока действует сам на себя [1]. Несмотря на обстоятельность и аккуратность проведенных экспериментальных исследований, подход к решению проблемы вызывает ряд вопросов. Кстати говоря, те же авторы сначала сделали заключение, согласно которому традиционную силу Био-Савара нельзя считать правильной [2], утверждая, что единственно справедливой является сила Ампера, удовлетворяющая правилу равенства и коллинеарности действия и противодействия (третьему закону Ньютона). Ссылаясь на результаты измерений, те же авторы по существу третий закон Ньютона в любой его формулировке, традиционной или обобщенной, поставили под сомнение. Такое же отношение можно обнаружить в других работах, посвященных выяснению природы и особенностей взаимодействия токов в классической электродинамике. Самым тяжеловесным утверждением является ссылка на невозможность существования в природе незамкнутых электрических токов [3]. Во-первых, это не так. Чтобы убедиться в этом, достаточно приглядеться к так называемой “однопроводной” передаче электрической энергии. Даже в ее банальной интерпретации, основанной на учете токов смещения, реальный электрический ток, правда переменный, но сравнительно низкой частоты, в проводнике все-таки течет [4]. Во-вторых, когда мы сомневаемся в справедливости третьего закона Ньютона, мы так или иначе рассматриваем часть замкнутого тока как некое тело, в принципе способное перемещаться относительно другого тела, в котором течет другая оставшаяся часть замкнутого электрического тока [5].
Вторым инфантильным аргументом считаются надуманные трудности в теоретическом рассмотрении взаимодействия объемных токов. Почему-то считается, что расходимости, присущие взаимодействию линейных токов [6], исчезают только для сил Ампера и Био-Савара, действующих между объемными токами [3].
Возникает подозрение, что субъективное неприятие нарушения принципа равенства и коллинеарности действия и противодействия спровоцировало кризис классической электродинамики. Судя по всему, нужен наглядный и реальный пример, который бы поставил точку в затянувшемся противоречии между полевой электродинамикой и неполевой интерпретацией Ампера.
Взаимодействие поверхностных токов
Прежде всего, нас будет интересовать сила Био-Савара F12, с которой одна часть цилиндра, скажем 1, действует на другую, обозначенную цифрой 2 на рис. 1. Предполагается, что тонкий цилиндр разделен на две в общем случае несимметричные части, по которым течет один и тот же постоянный ток I. При этом угол φ1 цилиндрической системы координат для первой части цилиндра заключен в интервале J<φ1<2p–J, тогда как угол φ2, определяющий положение элементов тока Idz2dr2 во второй ограничен интервалом –J<φ2<J. Поскольку положения элементов тока Idz1dr1 и Idz2dr2 определяются векторами
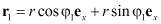 ,
,
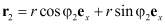 ,
,
и
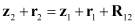 ,
,
то X – компонента сила F12 может быть записана следующим образом
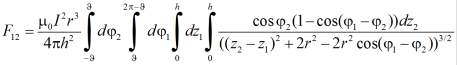 , (1)
, (1)
если r – радиус цилиндра и h – его высота. При записи выражения (1) использованы известное выражение
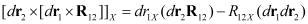 ,
,
для которого
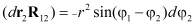 ,
,
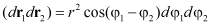 .
.
Интегрирование по z1 и z2 тривиально и дает
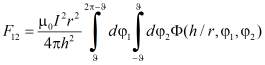 , (2)
, (2)
где
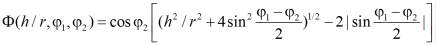 . (3)
. (3)
Аналогичное выражение можно записать для силы, с которой вторая часть цилиндра действует на первую
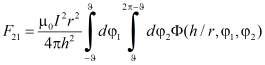 , (4)
, (4)
с той же самой подинтегральной функцией (3).
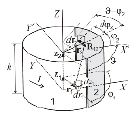
Рис. 1. Геометрия взаимодействия поверхностных цилиндрических токов
Возможны ли дальнейшие аналитические преобразования, направленные на сведение интегрирования к однократному? Конечно, возможны. Один из способов выполнить такую процедуру, это ввести переменные δ=(φ1−φ2)/2 и ϕ=(φ1+φ2)/2. Однако, получаемые в результате такой процедуры выражения настолько громоздки, что представить их здесь нет никакой возможности. В этом, впрочем, нет никакой необходимости. В конечном итоге все равно приходится проводить численный расчет. Пока же достаточно отметить, что ни одна из сил (2),(4) не расходится. Расходимость возможна лишь при h→0, что соответствует бесконечной плотности I/h поверхностного тока.
А теперь все внимание к рис. 2, где показаны силы действия и противодействия (2) и (4) при различных углах J. Самое основное: сумма сил F12 и F21 не равна нулю, что на первый взгляд противоречит не только законам сохранения энергии и импульса, но и здравому смыслу.
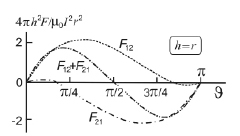
Рис. 2. Действие и противодействие в классической электродинамике поверхностных цилиндрических токов
Есть подозрение, что появилось неоднозначное отношение к тому, что изображено и что написано. Ошибочность расчетов, в том числе и численных, исключается полностью. Именно по этой причине, чтобы полностью исключить такие подозрения, предложен достаточно простой пример, а детали аналитических расчетов изложены настолько подробно, насколько это возможно. Остается единственная возможность привести расчеты в соответствие с законами сохранения: обратить внимание на физические явления, которые не были учтены.
Самодействие
Активное неприятие самодействия, то есть возможности механического воздействия тела самого на себя, судя по всему, связано с неопределенностью понятия силы. В рамках общей физики под силой понимают физическую причину, изменяющую состояние движения тел и возникающую в результате взаимодействия двух тел [7]. В рамках такого определения места силе самодействия нет, если под результатом взаимодействия двух тел обязательно понимается результат, характеризующий воздействие на данное тело других тел. Именно по этой причине мы склонны считать что сила инерции – это не сила, а «минус произведение массы тела на ускорение системы отсчета». Если же к понятию силы [7] относиться в более широком смысле, полагая, что сила всегда возникает при взаимодействии двух или нескольких тел и вовсе необязательно описывает воздействие на то или иное тело другого тела, то есть шанс увязать понятие силы самодействия с законами сохранения. В конце концов, в рамках теоретической физики мы под силой понимаем «минус градиент потенциальной энергии того или иного тела» [8].
Для того чтобы вычислить силу F22, с которой, скажем, вторая часть цилиндра воздействует сама на себя, вовсе необязательно проводить дополнительно аналитические преобразования. Совершенно очевидно, что
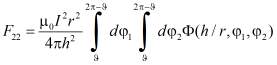 , (5)
, (5)
с сохранением всех результатов и обозначений, приведенных выше. Аналогично можно записать силу, с которой первая часть цилиндра с током действует сама на себя:
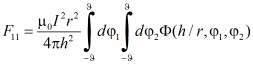 . (6)
. (6)
Можно пойти дальше и вычислить полную силу, действующую, например, на вторую часть цилиндра. Ее выражение оказалось даже более простым, чем те, что приведены выше:
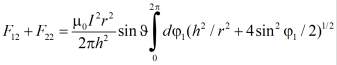 . (7)
. (7)
Не существует экспериментальной возможности отделить силу самодействия F22 от полной силы F12+F22. Поэтому есть все основания утверждать, что почти конечный результат (7) заслуживает несомненно большего внимания, чем то, что представлено ранее [1]. Рассматриваемый пример, безусловно, является более адекватным и для экспериментальной проверки, и для проведения численных расчетов.
Теперь возникло сомнение, что же на самом деле было выдано за результат измерения силы самодействия, если выделить это слагаемое из полной силы невозможно принципиально? На этот вопрос отвечает рис. 3, демонстрирующий результаты расчетов всех сил, действующих на все части тонкого цилиндра, по которому течет постоянный электрический ток, на всех основаниях считаемый поверхностным. Следует обратить внимание на области сравнительно малых или больших углов J, где вклад сил самодействия F11 или F22 является доминирующим. И еще:
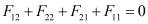 , (8)
, (8)
что в полном соответствии с законами сохранения импульса и энергии.
Действие и противодействие в неполевой электродинамике Ампера
У электротехники, которой досталась классическая электродинамика после того, как ею бросила заниматься фундаментальная наука, возникли очень большие проблемы с физикой. Основания для такого подозрения есть вполне обоснованные. К примеру, не будет электротехника заниматься теоремой о движении центра масс системы, в которой действуют силы самодействия. Для электромеханики проще разговор о существовании сил самодействия, как, впрочем, и о законе взаимодействия между элементами тока Био-Савара, объявить некорректной постановкой задачи [9], по непонятной причине полагая, что единственно корректной является неполевая формулировка Ампера, для которой сила взаимодействия элементов тока описывается формулой:
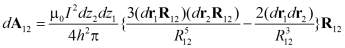 , (9)
, (9)
где
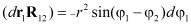 ,
,
и как прежде
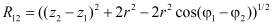 .
.
При этом почему то забывается, что закон Био-Савара имеет четкое теоретическое обоснование, опирающееся на специальную теорию относительности [10]. Небесконечность скорости передачи взаимодействия не только может, но и должна приводить к нарушениям третьего закона Ньютона в его традиционной формулировке. Раз уж на то пошло, то у теории относительности могут возникнуть претензии именно к формулировке Ампера. Тем не менее, несмотря на известные результаты [11-13], правило эквивалентности сил Ампера и Био-Савара остается противоречивым и недоступным, поэтому здесь должно быть проверено.
Со ссылкой на принятые выше обозначения и схему расчета вычисление X-компоненты силы Ампера A12, с которой первая часть цилиндра действует на вторую, может создать трудности только при проведении аналитических преобразований. Результата оказался ожидаемым, но сравнительно прозрачным:
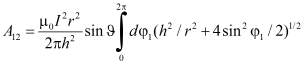 . (10)
. (10)
Нестоящая работа претендует по возможности на наиболее простое доказательство существования и реальности сил самодействия. Поэтому, сравнивая последний результат (10) с тем, что получено с учетом самодействия (7), можно утверждать, что задача решена полностью. А тот факт, что полная сила Ампера равна сумме сил действия и самодействия (рис. 3), не только это подтверждает, но и является независимой проверкой процедуры и принятой последовательности расчета и учета всего, что составляет те или иные силы.
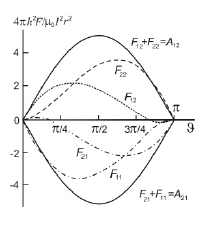
Рис. 3. Силы действия, противодействия и самодействия в классической электродинамике и неполевой формулировке Ампера

