Параметры кровообращения рассчитываются, с использованием значения объема желудочков и его необъективное значение может в целом повлиять на окончательный диагноз. Поэтому более точному измерению объема полости левого желудочка имеет важные значение при лечении и прогнозирование сердечно-сосудистых заболеваний. Разнообразие способов расчета объемов желудочковых камер вызвано сложностью их пространственной конфигурации. Это обусловливает необходимость представления полостей пространственной фигурой правильной геометрической формы. Такая модель позволяет рассчитать объемные показатели полости, имея лишь несколько ее линейных размеров. В основном, внимания исследователей сосредоточено на левом желудочке сердца, как имеющим наиболее правильную форму и наиболее хорошо доступному визуализацию. Самым распространенным способом расчета объема левого желудочка является расчет по формуле Тейчхольца (Teichholz) [1, 2, 3, 4, 5]:
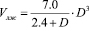, (1)
где D – переднезадний размер желудочка.
Существует способ расчета [2], основанный на эллипсоидной модели
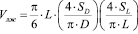, (2)
а также на основе представления левого желудочка в виде эллипсоида вращения
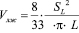, (3)
где SD, SL – площадь левого желудочка по длинной и короткой осям соответственно; D, L – размер полости левого желудочка по длинной и короткой осям соответственно. В зависимости от имеющейся патологии [3] для описания формы левого желудочка, также применяются гиперболоид, полусфера, усеченная сфера и другие фигуры вращения. Основными недостатками, перечисленными в [3, 5] и [2], являются, неадекватность отражения конфигурации нормального и патологического состояния сердца человека, несопоставимость результатов расчета объема одной полости разными методами и, как следствие, отсутствие единых критериев патологии. Наиболее близким к предлагаемому методу определения объемов полости левого желудочка, можно считать метод сечений; – разделение объема на n подобных объемов, проделанные в работе. Они основаны на анатомической особенности строения желудочковых камер. Заключающаяся в том, что форма внутреннего и внешнего контуров желудочков по короткой оси, несмотря на сложный характер, сохраняется на разрезе подобных фигур вдоль длинной оси сердца (перпендикулярно межжелудочковой перегородке) – правило подобия [2]. Наличие этой особенности подтверждает статистический анализ данных, полученных в результате патологоанатомических исследований серийных срезов сердца человека. Используя эту особенность, можно рассчитать объем желудочков сердца, имея лишь два сечения: по короткой и длинной осям, в терминах эхокардиографии – парастернально по короткой оси и апикальном с четырехкамерным доступом. Сущность способа состоит в следующем. Определяются площадь и длина полости в парастернальной позиции ультразвукового датчика по короткой оси на уровне конца митрального клапана. Далее ультразвуковой датчик устанавливается в апикальном с четырехкамерным доступом, изображение фиксируется. Исследуемая полость равномерно разбивается n параллельными линиями перпендикулярно межжелудочковой перегородке, с помощью штатных средств эхокардиографа, определяются размер желудочка по длинной оси и длина каждого отрезка, заключенного между точками пересечения внутреннего контура полости указанными линиями (рис. 1).
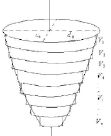
Рис. 1. Равномерное разбиение длинной оси на n отрезков, содержащих n криволинейного цилиндрического объема
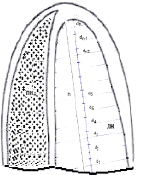
Рис. 2. Апикальная четырехкамерная позиция (предсердия не показаны)
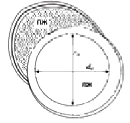
Рис. 3. Парастернальная позиция по короткой оси на уровне конца створк митрального клапана
В работе [2], имеется некоторые недостатки, так например;
- при вычислении объема учитывается подобные длины коротких осей, в разбиение длинной оси на n отрезок, а не площадь.
- предложенной формулы для определения объема полостей желудочков сердца не обосновано с математической точки зрения. Поэтому точность формулы оказывается невысокой.
Предлагаемый нами, здесь способ определения объема отличается от предыдущих исследование с тем, что здесь устранены все вышеперечисленные недостатки при сохранении точности расчетов. Сущность метода заключается в том, что сначала определяются площадь и длина полости в парастернальной позиции ультразвукового датчика по короткой оси, чуть ниже уровня митральных клапанов. Далее ультразвуковой датчик устанавливается в апикальном с четырехкамерным доступом. Изображение фиксируется, исследуемая полость по длинному осью равномерно разбивается n отрезок (рис. 2). Его средней точке, проводится параллельная линия, перпендикулярно межжелудочковой перегородке. Каждому короткому осью соответствуют определенные площади полости левого желудочка, которые также перпендикулярные межжелудочковой перегородке (рис. 3). Подобные площадь определяются с помощи формулы
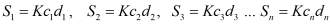, (4)
где K – коэффициент пропорциональности;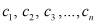 
– ординальные оси; 
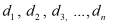– абсциссальные оси каждого; 
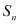– подобных плоских фигур, соответствующих n короткой оси желудочка. Из условия подобности Sn плоских фигур, вытекает, что
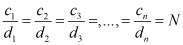. (5)
Отсюда легко находим
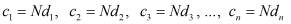(6)
Учитывая (6) в (4), определим
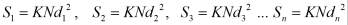(7)
Умножая каждый площадь, на длину отрезки и суммируя, их, найдем объем левого желудочки по формуле
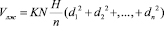(8)
KN – коэффициент определяется из любой выбранной площади подобной плоской фигуры (рис. 2), поэтому его найдем с помощью формулы
, 
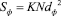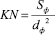. (9)
Подставляя (9) в (8), окончательно находим формулы для вычисления объема полости левого желудочка сердца
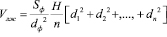, (10)
где dn – размер по короткой оси, проведенный средней точки n-ого отрезка перпендикулярно межжелудочковой перегородке; H – размер желудочка по длинной оси; dф – фиксирований размер полости в парастернальном доступе по короткой оси; Sф – фиксирований площадь полости в парастернальном доступе по короткой оси.
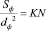– безразмерный геометрический коэффициент подобных плоских фигур. Для известных фигур, так например, для шара, эллипсоида, конуса, цилиндра, призмы коэффициент KN – имеет точные значение:
Для шара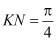 
, для эллипсоида 
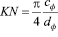, для конуса 
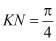, для цилиндра 
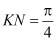, для призмы 
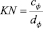и других известные геометрические фигуры можно определит конкретные значения KN.
Предложенная формула в работе [2] для вычисления объема полости левого желудочка, верны только при условии, когда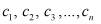 
коэффициенты равны между собой, то есть
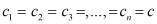. (11)
Умножая каждый площадь приведенные в формулы (4) , на длину отрезки и суммируя, их, при условии (11), найдем объем левого желудочки по формуле
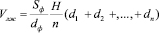. (12)
Однако (11) подобных плоских геометрических фигур не выполняется. Так как условия (11) доказывает также равенство других осей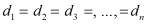 
n подобных фигур. Отсюда следует, что предложенная формула в работе [2] не правильно с математической точки зрения для плоских подобных фигур. Поэтому допускает существенные погрешности. Предложенный нами способ позволяет достичь следующего положительного эффекта:
- резкое уменьшение времени анализа данных эхокардиографического обследования;
- установление более точного измерения объема полости левого желудочка и надежно ставить диагноз для пациента.
- тестирование имеющейся известной геометрической фигуры (шар, конус, эллипсоид и др.) предложенной формулы, несколько раз точнее, чем в [2] Предложенный нами способ позволяет достичь следующего положительного эффекта:
- резкое уменьшение времени анализа данных эхокардиографического обследования;
- установление более точного измерения объема полости левого желудочка и надежно ставить диагноз для пациента.
- в тестирование имеющейся известной геометрической фигуры (шар, конус, эллипсоид и др.) предложенной формулы, пять раза точнее, чем предложенной формулы [2].
- предложенной формулы строго математически обоснованы, и каждый ее член имеет физический смысл.