Теория вероятностей и математическая статистика (стохастика) включена во многие школьные учебники математики и, хотя многие учителя математики пытаются обойти ее стороной она все же начинает занимать достойное место в учебном процессе.
Значительную помощь в организации процесса обучения стохастике оказывают информационно-коммуникационные технологии, и связано это с тем, что компьютер позволяет производить быстрые расчеты, организовывать «виртуальные математические эксперименты» и др.
Мы приведем лишь некоторые примеры использования информационно-коммуникационных технологий в обучении указанному учебному материалу.
Основными объектами, которые используются в азартных играх, являются монеты, игральные кости, колесо рулетки, карты и т. п. При проведении случайного эксперимента наступает случайный результат. Например, при подбрасывании монеты может выпасть или «герб», или «решка». В результате этого эксперимента может наступить любой из двух исходов, причем с равной вероятностью. Чтобы этот эксперимент реализовать с помощью компьютера, нужно использовать функцию, позволяющую сформировать случайное число в заданном диапазоне.
Выбрать случайное число из диапазона позволяет функция Random (язык программирования Beisik). Если эта функция записана без аргумента, то компьютер выбирает случайное действительное число из диапазона [0, 1).Если же в скобках указать аргумент, то компьютер выбирает случайное целое число из диапазона [0, аргумент).
Например, при подбрасывании монеты можно условиться, что исходу «герб» будет соответствовать число 1, а исходу «решка» − число 0. Таким образом, результатом эксперимента будет любое из двух целых чисел из диапазона [0, 2). Значит, команда, реализующая этот эксперимент, записывается следующим образом − RANDOM(2).
Если эксперимент состоит в подбрасывании игральной кости, то исходами могут быть значения от 1 до 6, и команда, реализующая этот эксперимент, записывается следующим образом: RANDOM(6)+1; 1 добавляется для того, чтобы сместиться от диапазона [0, 6) к реальному диапазону значений [1, 7).
Для реализации эксперимента с вращением колеса рулетки (европейской с 37 секторами) необходимо использовать команду: RANDOM(37).
Для осуществления многократного «подбрасывания» и подсчета числа исходов следует организовать цикл с параметром i, где i − счетчик совершенных подбрасываний.
Заметим, что сложнее обстоит дело с моделированием зависимых испытаний.
Задача. В урне пять черных и три белых шара. Два друга по очереди вынимают по одному шару, и побеждает тот, кому первому достанется белый шар, причем шары в урну не возвращаются. Найти шансы на победу каждого из игроков.
Решение. Для моделирования экспериментов такого типа предлагается сформировать строку, которая отображает текущее состояние урны. Обозначим буквой «б» белый шар и буквой «ч» черный шар. Тогда исходному состоянию урны будет соответствовать строка: «чччччббб». Чтобы смоделировать извлечение шара из урны, достаточно выбрать случайный символ из строки, а затем его из строки удалить. В случае, когда эксперимент проводится с возвращением шаров в урну, то выбранный символ из строки не удаляется.
Компьютерный эксперимент имеет и другие преимущества перед реальным. Существует много факторов, которые в реальном эксперименте могут привести к результатам, далеким от теории вероятностей: различная высота подбрасывания монеты, неровность поверхности, на которую она падает, несимметричность монеты, ловкость рук экспериментатора и т. п. Компьютер полностью исключает все эти факторы, то есть мы можем говорить о чистоте и объективности компьютерного эксперимента, который проводится как бы в идеальных условиях.
В наших работах [1, 2, 3, 4] приведено большое число примеров по использованию информационных технологий в обучении теории вероятностей и математической статистике.
Если учитель будет использовать книгу [1] на элективных курсах для работы с учащимися, то предполагается, что они должны быть знакомы с элементарной теорией вероятностей, когда за основные неопределяемые понятия взяты «испытание», «исходы испытания». Каждое испытание заканчивается только одним из исходов, множество которых (конечное или счетное) называется пространством элементарных событий. С каждым исходом wk связывается неотрицательное число pk − вероятность этого исхода, при этом сумма всех таких вероятностей равна 1. Случайное событие A − это подмножество пространства элементарных событий. Если исход, то говорят, что он благоприятствует событию A. Его вероятность определяется как сумма
,
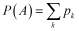где суммирование идет по всем k, для которых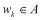 
. В частном случае, когда множество исходов конечное и все они равновероятные, то есть 
, получаем классическое определение вероятности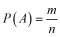 
, где m − число благоприятных исходов, а n − число всех исходов.
Вопрос о том, как определяются численные значения вероятностей pk в данной конкретной задаче, решается либо в результате большого числа наблюдений, либо возможно предсказание вероятностей в ходе испытания на основе симметрии, в результате чего приходят к классическому определению. Так, если испытание состоит в подбрасывании игрального кубика, то можно с вероятностью 1/6 ожидать выпадение на каждую из своих шести граней.
Наличие у события A вероятности p может быть проверено экспериментально, когда подсчитывается относительная частота m/n его появления в достаточно длинной серии n испытаний. В различных работах приведены результаты экспериментов по проверке «симметричности монеты», проведенных рядом исследователей. Последуем вслед за ними и «покидаем» монету на компьютере в качестве упражнения на освоение Mathcad.
Условимся, выпадение герба интерпретировать числом 1, а нулем − выпадение цифры. В достаточно длинной последовательности из случайных нулей и единиц подсчитаем долю единиц, используя встроенную функцию Хевисайда Ф(x). Для получения случайных чисел 0, 1 сгенерируем случайное число между 0 и 1 командой rnd(1), которое затем округлим в ближайшую сторону командой round(x). Полученный вектор X из нулей и единиц можно просмотреть прокруткой.
Результат должен подтвердить, что предположение о равновозможности герба и цифры находится в согласии с опытом.
Аналогично экспериментально можно проверить, что с вероятностью 1/6 выпадет шестерка при подбрасывании игрального кубика. Для этого надо уметь сгенерировать случайное число из множества {1,2,3,4,5,6}. Например, найти целую часть (команда floor) случайного числа rnd(6) между 0 и 6, к которой добавить 1.
Статистические закономерности такого рода были обнаружены давно на примерах карточных игр, игр в кости и т.п., то есть на примерах испытаний, которые характеризуются равновозможностью исходов. Эти наблюдения открыли путь для статистического подхода к численному определению вероятности.
Компьютерный эксперимент особенно важен, когда из теоретических соображений значение вероятности заранее установить нельзя.
По численным значениям элементарных событий, найденным классическим или статистическим способом, могут быть найдены новые вероятности по соответствующим теоремам сложения или умножения. Они достаточно хорошо освещены в учебной и методической литературе.
С.В. Щербатых [5] замечает, что при обучении стохастике требуется наглядное представление о влиянии случайностей на стохастические выводы в ходе произведенных опытов. В связи с этим необходима поддержка стохастической содержательно-методической линии школьного курса математики информационными системами. Рассмотрим некоторые из них.
- Обучающая программа «Математика (5-11 классы)», разработанная издательством «Дрофа ДОС» в 2003 году и выпущенная на CD-диске.
- Электронное издание «Математика, 5-11 классы. Практикум», разработанное ГУ РЦ ЭМТО, ЗАО «1С», АН О УИЦ «Интерактивная линия» в 2004 г. и выпущенное на СD-диске.
- Электронный учебник «StatSoft» (http://www.statsoft.ru /home/textbook) помогает начинающим изучать статистику, в первую очередь, старшеклассникам, усвоить основные понятия статистики и более полно представить диапазон применения статистических методов.
К числу основных вопросов, на которые ученик может получить ответ пользователя, относятся следующие: «Что такое переменные?», «Что такое статистическая значимость?», «Почему объем выборки влияет на значимость зависимости?» и т.д.
Наиболее адаптированными для поддержки изучения стохастической линии школьного курса математики в старших классах общеобразовательной школы являются программы: GRAN – 1, Maple, MathCad, Mathematika, Mathlab, Maxima, SPSS, STATISTICA, Statgraph и др..
Наиболее адаптированными к школе являются GRAN – 1, SPSS, STATISTICA.
Для нахождения числовых характеристик (минимум, максимум, среднее, дисперсия, среднее квадратичное отклонение и т.д.) можно использовать разведочный анализ Explore.
Список сайтов и программ можно продолжить и далее, но мы ограничились данными, поскольку считаем, что они помогут составить основательную базу при изучении элементов теории вероятностей и математической статистики с привлечением адаптированных для старшеклассников электронных средств прикладного назначения.