Задачи, связанные с образованием газогидратов, в настоящее время представляют значительный научный и практический интерес, что обусловлено перспективой использования газовых гидратов в различных технологиях [1, 4].
В данной работе рассматривается образование газогидрата в насыщенном газом и водой пористом пласте конечной протяженности при закачке холодного (с температурой меньшей исходной температуры пласта) газа. В работах [2, 3, 5-9] данная задача решалась в автомодельной постановке. Такая постановка применительно к задаче об образовании газовых гидратов в пористых пластах конечной протяженности соответствует начальному этапу процесса, когда влияние границ пласта несущественно.
Постановка задачи и основные уравнения. Рассмотрим горизонтальный пористый пласт (x ≥ 0) длины L, насыщенный в начальный момент времени газом (метаном) и водой. Давление p0 и температура T0 пласта соответствуют условиям существования их в свободном состоянии, т.е. p0 < ps0, где ps0 = ps(T0) – равновесное давление гидратообразования, соответствующее исходной температуре T0. Пусть в момент времени t = 0 через левую границу пористого пласта (x = 0) начинается закачка газа (одноименного исходному) под давлением pe и температурой Te. Причем величины pe и Te соответствуют условиям стабильного существования гидрата (pe > ps(Te)). Требуется определить изменение во времени полей давления, температуры и гидратонасыщенности в пласте при t > 0.
При нагнетании газа в пористой среде возможно образование трех областей: ближней, примыкающей к границе нагнетания, в которой поры заполнены газом и гидратом; промежуточной, где газ, гидрат вода находятся в состоянии термодинамического равновесия и происходит процесс образования гидрата, и дальней, которая заполнена газом и водой. Промежуточную область будем называть гидратной волной. Соответственно могут возникнуть две фронтальные границы: между ближней и промежуточной областями (ближняя граница), где оставшаяся вода в объемной области полностью перешла на этой границе в состав гидрата, и между дальней и промежуточной областями (дальняя), на которой начинается процесс гидратообразования. Такое положение соответствует начальному этапу процесса образования газогидрата, когда влияние правой границы (x = L) не существенно. Однако в ходе дальнейшей эволюции, объемная область может вырождаться во фронтальную поверхность, на которой полностью происходит образование газогидрата из находящейся в пористой среде воды перед фронтом.
Для описания процессов тепло- и массопереноса при нагнетании в пласт газа, сопровождающееся образованием газовых гидратов, примем следующие допущения: пористость постоянна, скелет пористой среды, вода, газогидрат несжимаемы и неподвижны, газ калорически совершенный:
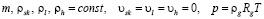 .
.
Здесь и далее индексы sk, l, g, h относятся к параметрам скелета пористой среды, воды, газа и гидрата соответственно; m – пористость, ρj и υj (j = sk, l, h) соответственно истинная плотность и скорость j-й фазы, p – давление, T – температура, Rg – газовая постоянная,. Будем полагать, что процесс однотемпературный, т.е. температура пористой среды и насыщающего ее вещества (газа, воды и гидрата) в каждой точке совпадают. Гидрат является двухкомпонентной системой с массовой концентрацией газа G.
С учетом сделанных допущений уравнения сохранения масс газа и воды в плоскоодномерном случае можно записать в виде [5]:
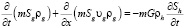 ,(1)
,(1)
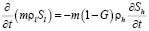 , (2)
, (2)
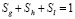 , (3)
, (3)
где Sj (j = g, h, l) –насыщенности пор j-й фазой, υg – скорость газовой фазы.
Фильтрация газа описывается законом Дарси:
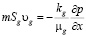 . (4)
. (4)
Уравнение притока тепла, пренебрегая баротермическим эффектом, можно записать в виде:
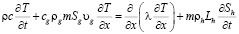 . (5)
. (5)
Здесь
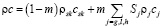
и 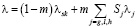 –
–
удельная объемная теплоемкость и теплопроводность системы, cj и λj – удельная теплоемкость и теплопроводность j-й фазы, Lh – удельная теплота разложения газогидрата.
Так как основной вклад в величины ρc и λ вносят параметры скелета пористой среды, то будем полагать их постоянными и равными:
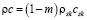 ,
, 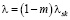 .
.
Зависимость коэффициента проницаемости для газа от газонасыщенности, зададим на основе формулы Козени [8]:
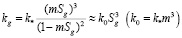 , (6)
, (6)
где k0 – абсолютная проницаемость пласта.
Температура и давление в области существования гидрата связаны условием фазового равновесия [4]:
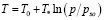 , (7)
, (7)
где T0 – исходная температура системы, ps0 – равновесное давление, соответствующее исходной температуре, T* – эмпирический параметр, зависящий от вида газогидрата.
При образовании газогидрата в пористом пласте возникают зоны, в которых газ, гидрат и вода могут находиться в различных состояниях. Поэтому на границах между этими зонами, являющихся передним и задним фронтом гидратной волны, для потока массы и тепла, должны выполняться следующие законы сохранения:
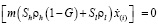 ,
,
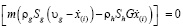 , (8)
, (8)
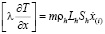 .
.
Здесь [f] – скачок величины f на границе x(i) между областями, 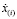 – скорость движения границы фазового перехода; индексы i = n и d соответствуют ближней и дальней границам. Температуру и давление на них будем полагать непрерывными.
– скорость движения границы фазового перехода; индексы i = n и d соответствуют ближней и дальней границам. Температуру и давление на них будем полагать непрерывными.
Из уравнения неразрывности для воды (3) имеем:
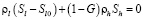 , (9)
, (9)
где Sl0 – начальная водонасыщенность пористой среды. Тогда, учитывая соотношение (3), получаем:
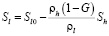 ,
,
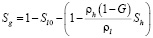 .
.
На правой границе пласта (x = L) поставим условия, моделирующие отсутствие кондуктивного потока тепла и постоянное, равное p0, давление:
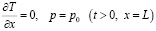 .
.
Начальные условия примем в виде:
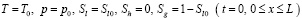 .
.
Решение с фронтальной границей фазовых переходов. Предположим при нагнетании газа в пористом пласте возникают две области. В первой (0 ≤x < x(n)), находящейся вблизи границы пласта, вода полностью перешла в гидратное состояние, поэтому в порах присутствует только газ и газогидрат. Во второй, дальней области (x(n) < x ≤ L), поры заполнены газом и водой. Таким образом, согласно принятой модели образование гидрата происходит только на фронтальной поверхности (x = x(n) ), а промежуточная область отсутствует.
Используя соотношения (1)–(7), можно получить следующие уравнения пьезо- и теплопроводности, описывающие распределения давления и температуры в обеих областях:
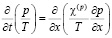 ,
,
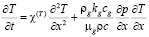 (11)
(11)
где 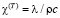 и
и 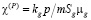 – коэффициенты температуропроводности и пьезопроводности.
– коэффициенты температуропроводности и пьезопроводности.
На поверхности, разделяющей ближнюю и дальнюю области, происходит скачок гидратонасыщенности от 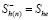 до
до 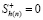 , а гидратонасыщенность первой области определяется из условия (9):
, а гидратонасыщенность первой области определяется из условия (9):
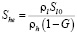 (12)
(12)
Давление и температура на границе между областями связаны условием фазового равновесия (7).
Из (8) с учетом соотношения (4) запишем систему уравнений для нахождения основных параметров пласта на границе фазового перехода x = x(n) :
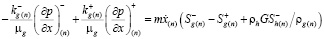 , (13)
, (13)
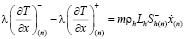 ,
,
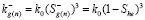 ,
, 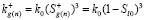 .
.
Верхними индексами «минус» и «плюс» снабжены терпящие разрыв параметры перед и за границей.
Для решения задачи (11) с граничными условиями (13) введем равномерную сетку с шагом h. Так как решение ищется в областях с неизвестной границей фазовых переходов (x = x(n) ), то использовался метод ловли фронта в узел сетки, причем из уравнений (11) находятся распределения давления и температуры в обеих областях, а давление, температура на границе, а также шаг временного слоя находятся из (13).
Результаты численных расчетов. На рис. 1 представлена зависимость координаты границы фазового перехода от времени при нагнетании газа под давлением ре = 5 МПа и температурой Те = 278 К в пласт длины L = 1 м. Исходные параметры системы полагались равными р0 = 4 МПа, Т0 = 280 К, Sl0 = 0.2; абсолютная проницаемость и пористость пласта – k0 = 10-14 м2, m = 0.1. Для остальных параметров, характеризующих систему, приняты следующие значения: G = 0.12, T* = 10 К, ps0 = 5.5 МПа, приведенная газовая постоянная
Rg=520 Дж/(К∙кг),
плотности
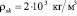 ,
, 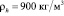 ,
,
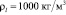 ,
,
удельные теплоемкости
сsk = 1000 Дж/(К∙кг), сh = 2500 Дж/(К∙кг), сl = 4200 Дж/(К∙кг), cg = 1560 Дж/(К·кг),
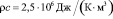 ,
,
коэффициенты теплопроводности
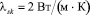 ,
, 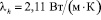 ,
,
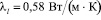 ,
,
вязкость газовой фазы 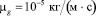 , удельная теплота гидратообразования Lh = 5·105 Дж/кг. При данных параметрах нагнетаемого газа образование гидрата в режиме продувки происходит на фронтальной границе. Из рисунка следует, что поверхность фазового перехода движется только до некоторого положения
, удельная теплота гидратообразования Lh = 5·105 Дж/кг. При данных параметрах нагнетаемого газа образование гидрата в режиме продувки происходит на фронтальной границе. Из рисунка следует, что поверхность фазового перехода движется только до некоторого положения 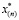 , затем ее движение прекращается (происходит остановка). При этом в пласте область
, затем ее движение прекращается (происходит остановка). При этом в пласте область 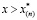 содержит лишь газ и воду, а область
содержит лишь газ и воду, а область 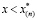 – только газ и гидрат.
– только газ и гидрат.
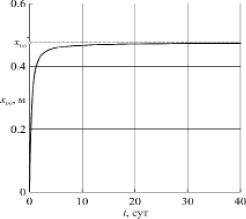
Рис. 1. Зависимость координаты границы фазового перехода от времени при продувке пласта газом: ре = 5 МПа, Те = 278 К
Для объяснения такого поведения движения границы x = x(n) рассмотрим представленные на рис. 2 фазовую диаграмму и распределение давления в пласте. На рис. 2 а пунктирная кривая определяет условие фазового равновесия между газом, водой и газогидратом. Точкой «0» изображено состояние, соответствующее начальному состоянию пористой среды, точкой «e» – условие на ее левой границе (x = 0). Как видно из рисунка в момент времени t = 887 ч температура во всем пласта становится равной температуре нагнетаемого газа. При этом профили давления и однозначно связанной с ним равновесной температуры, как следует из рис. 2 б, имеют вид прямой убывающей вглубь пласта. Поэтому, существует такая точка 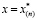 , в которой равновесная температура совпадает с температурой пласта. При этом в области
, в которой равновесная температура совпадает с температурой пласта. При этом в области 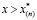 параметры системы будут соответствовать условию стабильного существования газа и воды, а в области
параметры системы будут соответствовать условию стабильного существования газа и воды, а в области 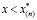 – газа и гидрата.
– газа и гидрата.
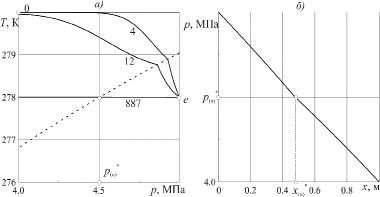
Рис. 2. а – фазовая диаграмма процесса образования гидрата при продувке пласта газом; б – распределение давления в пласте в момент времени t = 887 ч. Пунктирная линия – равновесная температура пласта.Числа на кривых – время в часах
Таким образом, из рассмотренной фазовой диаграммы следует, что для гидратации пористой среды без остановки границы фазового перехода необходимо, чтобы температура нагнетаемого газа Те удовлетворяла условию:
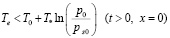 .
.
Выводы. Методом ловли фронта в узел сетки получено численное решение задачи об образовании газогидрата в пористой среде конечной протяженности при инжекции холодного газа. Показано, что если температура нагнетаемого газа больше, чем равновесная температура гидратообразования, то образование гидрата в некоторой точке пласта прекращается, т.е. образуется «висячий» скачок гидратообразования.
Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований в рамках проекта 14-01-31089 мол_а.

