Кислотная обработка пористых сред, является одним из эффективнейших способов увеличения фильтрационных свойств скелета. Имеется значительное количество работ, в которых исследуются особенности взаимодействия реагента с пористым телом [1-3]. В большинстве известных математических моделей изменение пористости коллектора определяется по количеству породы, растворенной в кислоте, а изменение проницаемости – по формуле Козени-Кармана [3, 4], связывающей проницаемость с пористостью.
Новизна работы заключается в методе вычисления изменения фильтрационных свойств пористой среды, основанном на моделировании динамики функции распределения пор по размерам исследуемого образца в результате растворения породы с учетом интенсивности объединения поровых каналов.
Постановка задачи. Основные уравнения
Рассматривается двухфазная трехкомпонентная (нефть, вода, кислота) изотермическая фильтрация несжимаемых несмешивающихся жидкостей в недеформируемом пористом теле. Моделируется кислотное воздействие на пористую среду, при этом считается, что концентрация кислоты мала.
Законы сохранения двухфазной трехкомпонентной фильтрации можно записать в виде уравнений неразрывности для нефти и воды [5]
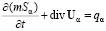, (α=o,w); (1)
уравнения неразрывности для кислоты [4]
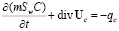; (2)
уравнений движения для нефти, воды и кислоты:
, 
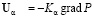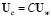. (3)
В приведенных выше соотношениях α=o,w, где индексами «o» и «w» помечены параметры нефтяной и водной фазы,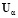 
– скорость фильтрации фазы α, P – давление в фазах, 
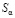– насыщенность пористого тела фазой α (
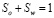), С – концентрация кислоты, m – пористость, 
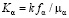, k – абсолютная проницаемость, 
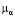– динамическая вязкость, fα – функция относительной фазовой проницаемости, qw – интенсивность образования воды в результате химической реакции (карбоната кальция и соляной кислоты), qc – источник, характеризующий уменьшение массы кислоты в результате ее реакции с породой.
Уравнение химической реакции взаимодействия соляной кислоты с карбонатной породой имеет виде:
СаСО3 + 2НСl = CaCl2 + CO2+Н2О. (4)
В результате реакции растворившийся объем элемента пористой среды будет замещен продуктами реакции (правая часть уравнения). Так как одним из образующихся веществ будет вода (со стехиометрическим коэффициентом равным одному), можно принять, что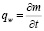 
.
Пусть процесс фильтрации происходит в области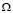 
, с границей Г, состоящей из трех частей – Г1, Г2, Г3. Будем считать, что для начального момента времени известно распределение водонасыщенности и концентрации:
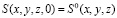
и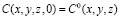 
.
На участке границы Г1 (входная часть границы) будем считать известными давление, насыщенность и концентрацию кислоты:
, 
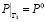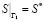и 
.
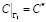На участке границы Г2 (выходная часть границы) будем считать заданным давление:
.
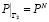Часть границы Г3 будем считать непроницаемой:
.
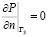В общем случае величины P0, S*, PN и C* могут зависеть от координат и от времени. В рассмотренном ниже примере насыщенность и давление на Г1, а также давление на Г2 считаются постоянными, т.е. P0, S*, PN – const. Во время поступления кислоты в образец С*=1, в любое другое время С*=0. Если через какую-то часть участка границы Г1 кислота в пористую среду не поступает, то на этой части С*=0.
Построенная система уравнений решается в переменных давление, насыщенность и концентрация кислоты конечно-элементным методом контрольных объемов на равномерной сетке. Методы аппроксимации и численная схема решения задачи подробно описаны в работе [6].
Для того, чтобы описать изменения фильтрационно-емкостных характеристик пористой среды, воспользуемся функцией распределения пор по размерам 
. В начальный момент спектр пор в каждой точке пласта считается известным: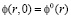 
; его изменение во времени подчинено следующему уравнению [6]:
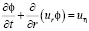. (5)
где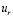 
– скорость изменения радиуса пор и uη – интенсивность объединения поровых каналов. Скорость изменения радиуса порового канала определяется по формуле 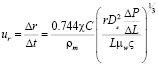[6]:
, (6)
где De – коэффициент эффективной диффузии, ρm – плотность породы, L – длина капилляра, r – радиус капилляра, χ – стехиометрический коэффициент, ς – извилистость капилляра.
Элементарный процесс объединения двух поровых каналов будем рассматривать как их слияние и опишем при помощи уравнения М. Смолуховского:
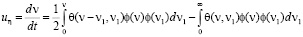. (7)
Неотрицательную функция θ называют ядром объединения.
Изменение фильтрационно-емкостных характеристик пласта вычисляется на основе смещения функции распределения пор по размерам при помощи следующих выражений:
,
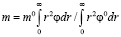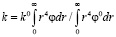(8)
где k0,m0 – начальные значения проницаемости и пористости соответственно.
Одним из основных достоинств такого определения пористости и проницаемости является возможность предсказания появления «червоточин» (пор большого размера) в пористой среде по динамике функции распределения пор по размерам.
Результаты исследований
Рассмотрим одномерную задачу по кислотному воздействию на пористую среду. Рассматриваемый образец представляет собой прямоугольную область размерами 1×0.1 м единичной толщины. В начальный момент времени пористая среда заполнена нефтью. Начальная проницаемость k=0.10 мкм2, начальная пористость m=0.08. Динамические вязкости нефти и воды µo= 35 мПа×с, µw= 1.5 мПа×с соответственно.
Через левое сечение проводится нагнетание воды вместе с кислотой, а через правое сечение происходит отбор жидкости. На входе в образец поддерживается постоянное значение давления Pin=1.01 МПа, а на выходе – Pout=1 МПа. Длительность нагнетания оторочки составляет 2.5 сут. Концентрация кислоты в растворе 5 %.
На рис.1 показана функция распределения пор по размерам в узле с координатами (1,1) для трех моментов времени. Начальный спектр пор по размерам был взят из работы Котяхова [7] (рис.1 – «0 сут»). Вследствие химической реакции кислоты с поверхностью капилляра его радиус увеличивается, что отражается в смещении графика функции распределения в сторону больших радиусов (рис. 1 – «1 и 2 сут»).
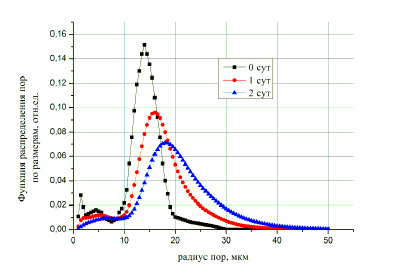
Рис. 1. Изменение функция распределения пор по размерам в результате кислотной обработки
Будем считать, что каналы, радиус которых больше 500 мкм, являются червоточинами. Пусть N – общее число поровых каналов в контрольном объеме. Тогда количество червоточин в этом объеме можно вычислить по формуле:
.
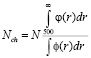По расчетам во входном сечении моделируемого образца после кислотной обработки образуются 2 канала с радиусами более 500 мкм.
Как было отмечено, длительность нагнетания кислотной оторочки составляет 2.5 сут. Перемещение закачанной оторочки активной примеси к выходному сечению сопровождается постепенным уменьшением количества содержащейся в ней кислоты из-за ее реакции с пористой средой (рис. 2).
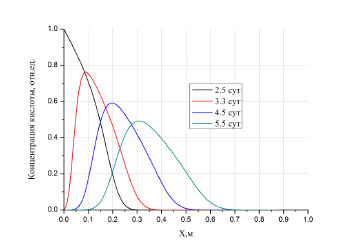
Рис. 2. Профиль течения кислотной оторочки на различные моменты времени
В результате химической реакции кислоты со скелетом, будут изменяться фильтрационно-емкостные параметры пористой среды. Ниже на различные моменты времени представлены профили распределения абсолютной проницаемости (рис. 3) (профиль пористости на различные моменты времени будет иметь идентичный вид с точностью до численных значений).
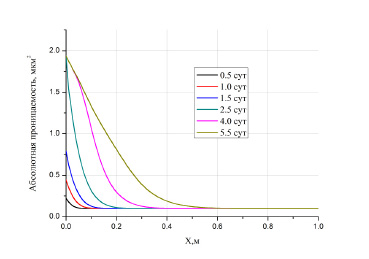
Рис. 3. Профиль абсолютной проницаемости на различные моменты времени
Как видно из приведеных графиков, наиболее сильному воздействию подвергается область вблизи входного сечения образца. По мере удаления от источника кислотного реагента изменения фильтрационно-емкостных характеристик менее выражены. Пористость и проницаемость не будут изменяться в тех областях, куда кислота не попала.
Выводы
В работе представлена математическая модель вытеснения нефти водой с применением кислотного воздействия на пласт, в которой для описания изменения фильтрационно-емкостных характеристик коллектора использована модель идеальной пористой среды в виде пучка капилляров различных радиусов. Учтена зависимость скорости химической реакции от скорости фильтрации воды.
Используя описанную модель, приведены результаты, характеризующие основные «последствия» от кислотной обработки пористой среды. Рассчитано количество «червоточин» во входном сечении образца; показано, что максимальное изменение пористости и проницаемости наблюдается в области с наибольшей концентрацией кислоты.
Работа выполнена за счет средств субсидии, выделенной в рамках государственной поддержки Казанского (Приволжского) федерального университета в целях повышения его конкурентоспособности среди ведущих мировых научно-образовательных центров, за счет субсидии, выделенной Казанскому федеральному университету для выполнения государственного задания в сфере научной деятельности, а также гранта РФФИ № «14-01-31096 мол_а»