В настоящее время применяемые методы моделирования температурных полей основаны детерминированном подходе, при котором параметры теплового режима являются строго определенными. Вместе с тем практика проектирования и эксплуатации реальных систем показывает, что допущение о детерминированности является неадекватным, потому что приводит к результатом весьма далеким от действительности. К данному обстоятельству приводят следующие факторы:
- случайный технологический разброс изготовления элементов системы;
- случайный характер параметров окружающей среды (температуры, влажности, скорости теплоносителей и пр.);
- случайный характер внешних условий эксплуатации (напряжений электропитания, мощностей тепловыделения и т.д.);
- случайный характер параметров конструкции системы (величина контактных зазоров, размеров, формы, расстояний между элементами и пр.).
Случайный характер этих и других факторов тепловых режимов технических систем, приводит к тому, что различные экземпляры одной и той же «идентичной» технической системы, построенных на «идентичных» элементах, будут иметь различные распределения температуры. Поскольку все случайные факторы, определяющие тепловой режим системы, изменяются внутри интервалов своих допустимых значений, постольку их неопределенность носит интервальный стохастический характер, так же как и неопределенность распределений температуры. Моделирование интервально стохастических температурных полей необходимо как для повышением адекватности моделирования, так и для анализа причин неправильного функционирования и срабатывания системы, выхода из строя, потери устойчивости, выхода эксплуатационных параметров за пределы своих допусков. [7].
Проблема моделирования стохастических температурных полей в технических системах рассматривалась в литературе, например, [1, 3, 9, 10], однако до сих пор отсутствуют адекватные и эффективные математические и компьютерные методы численного моделирования стохастических температурных полей в технических системах, что обусловливается как значительными математическими трудностями, так и с априори неизвестной сходимостью искомых моментов стохастического температурного поля к истинным значениям.
В настоящей статье приводится метод моделирования интервально стохастических температурных полей, обусловленных интервальным характером входных данных, определяющих тепловые режимы технической системы. Входные данные представляют собой случайные величины, равномерно распределенные внутри интервалов своего изменения. Алгоритм метода моделирования основывается на матрично-топологическом методе [2, 3, 5], реализации его в программном комплексе моделирования температурных полей технических систем STF-ElectronMod [5, 11] и методе статистических испытаний [6]. Практическое сравнение разработанного метода с методом интервального анализа, показало, что результаты, получаемые с помощью интервальной арифметики, приводят к неоправданно широким интервалам температур, неадекватным реальность. Применение разработанного метода продемонстрировано на примере моделирования температурного поля электронной системы.
Метод и алгоритм моделирования температурных полей в условиях интервальной неопределенности
Тепловая модель технической системы представляет собой область Q с границей Г, состоящую из N различных подобластей Qi с границей Гi, которые отображают элементы технической системы (ТС):
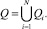
Элементы ТС находятся в контакте между собой и в состоянии теплообмена с окружающей средой как внутри ТС, так и вне ее.
В общем случае теплофизические и конструктивные факторы, определяющие температурное поле ТС и ее элементов, такие как теплофизические характеристики материалов, мощности тепловыделения элементов ТС, тепловые контактные сопротивления, величины зазоров между элементами, температуры и скорости среды и другие факторы и условия, являются интервальными, изменяющимися в пределах границ своих допустимых значений и при этом являются случайными величинами, равномерно распределенными внутри интервалов. В результате тепловой режим и температурное поле ТС и ее элементов будут носить стохастический характер.
Математическая модель, описывающая стохастическое стационарное температурное поле T(ω) = T(x, y, z, ω) в тепловой расчетной области Q для каждого элементарного события ω из пространства элементарных событий Ω (ω ∈ Ω), может быть записана в виде:
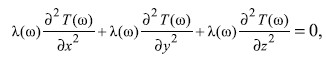(1)
где λ(ω) = λ(x, y, z, ω) – стохастический коэффициент теплопроводности материалов области Q, являющегося кусочно-постоянной функцией в каждой из подобластей.
Граничные условия на границах подобластей Гi соответствуют теплообмену с поверхности подобласти-элемента Qi (границы подобласти Гi) в среду и совместному действию поверхностного источника тепла на границе:
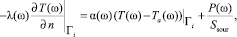(2)
где α(ω) = α(x, y, z, ω) – стохастический коэффициент теплоотдачи (кусочно-постоянный) с поверхности подобласти Гi в среду; Ta(ω) = Ta(x, y, z, ω) – стохастическая температура среды возле границы подобласти Гi; P(ω) = P(x, y, z ,ω) – стохастическая величина поверхностной мощности источника тепла, распределенного в области площадью Ssour и расположенного на границе Гi подобласти (элемента ТС); n – нормаль к поверхности.
Параметры θ(ω) = (θ1(ω), θ2(ω), …, θn(ω)), определяющие тепловые режимы ТС – коэффициенты теплопроводности материалов, коэффициенты теплоотдачи с поверхностей элементов, температуры среды внутри и снаружи ТС, мощности тепловыделений элементов, контактные тепловые сопротивления и другие параметры конструкции ТС – в общем случае являются интервальными, как имеющие допуска проектировании и изготовлении. Другими словами, они изменяются внутри своих интервалов допустимых значений и являются случайными величинами равномерно распределенными внутри интервалов. Это означает, что все параметры ТС из вектора θ(ω) = (θ1(ω), θ2(ω), …, θn(ω)) будучи интервально стохастическими изменяются в интервалах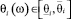 
, где 
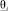и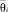 
– нижняя и верхняя границы интервала, и при этом параметр θi(ω), ω ∈ Ω, является случайной величиной с равномерной плотностью вероятности:
p = 1/Δi, если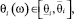 
p = 0, если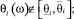 
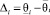– ширина интервала.
Поскольку математическая модель (1), (2) является стохастической, то решение уравнений модели будет представлять собой стохастическое температурное поле T(ω) = T(x, y, z, ω), в каждой точке которого температура будет интервальной случайной величиной. В результате решения стохастической математической модели (1), (2) должны быть определены следующие поля статистических мер стохастического температурного поля T(ω) = T(x, y, z, ω) в области Q:
- поле математических ожиданий температур
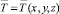; - поле дисперсий D(x, y, z) рассеяния случайных значений температур вокруг математического ожидания;
- поле средних квадратических отклонений σ(x, y, z) температурного поля (D(x, y, z) = ϭ2(x, y, z));
- поля границ интервалов стохастического температурного поля – нижней Tmin(x, y, z) и верхней Tmax(x, y, z) границ, между которыми могут изменяться все случайные реализации температуры для всех ω ∈ Ω в каждой точке области Q. Поля границ интервалов Tmin(x, y, z) и Tmax(x, y, z) соответствуют границам доверительных интервалов, которые с некоторой доверительной вероятностью Рдов накрывают возможные истинные значения температур, которые могут иметь место на практике в ТС
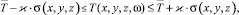
где ϰ – множитель, изменяющийся в диапазоне от 1 до 3 в зависимости от величины принятой доверительной вероятности Рдов.
Метод моделирования интервально стохастических температурных полей ТС основывается на матрично-топологическом методе моделирования трехмерных температурных полей многослойных структур [3–5], компьютерную реализацию метода в виде программного комплекса (ПК) моделирования трехмерных детерминированных температурных полей электронных систем STF-ElectronMod [5, 11] и метод статистических испытаний [6]. Алгоритм метода состоит из трех этапов основных этапов.
Этап 1
Вводятся исходные данные, полностью характеризующие конструкцию ТС, условия ее теплообмена внутри и вне ТС, эксплуатационные параметры ТС, мощности потребления, расположение источников тепла, контактные тепловые сопротивления, теплофизические параметры материалов, координаты и размеры элементов ТС, условия монтажа и пр. Для входных данных, являющихся интервально стохастическими, задаются нижние и верхние границы интервалов их изменения. По введенным данным осуществляется расчет усредненных температур и мощностей всех элементов в ТС, взаимодействующих между собой. Расчеты проводятся по матрично-топологическому методу с помощью программного комплекса STF-ElectronMod [5, 11]. По процедуре статистических испытаний производится разыгрывание множества реализаций стохастических входных данных и накапливается статистика для расчетов статистических мер усредненных температур и мощностей источников и стоков тепла в ТС.
Этап 2
Включает вычисления статистических мер усредненных температур и мощностей элементов ТС – математических ожиданий (МО), дисперсий (Д), средних квадратических отклонений (СКО), границ интервалов, внутри которых изменяются реализации усредненных температур и мощностей и матрица ковариаций стохастической связи между мощностями источников и стоков.
Этап 3
Определяются искомые температурные полей статистических мер: математических ожиданий, дисперсий, средних квадратических отклонений, границ интервалов, покрывающих при заданной доверительной вероятности возможные значения стохастических температур, которые могут иметь место на практике.
Необходимо отметить, что в алгоритме применяются авторские методы и оптимизированная структура программного комплекса STF-ElectronMod, которые позволяют осуществлять вычисления полей статистических мер температуры в ТС в пределах 1 мин на desk РС Pentium, при числе реализаций 10000 и точности моделирования не выше 3 %.
Разработанный в статье метод применялся для компьютерного моделирования интервально стохастических температурных полей в электронной системе (ЭС), включающей многослойную печатную плату (МПП), установленные на ней 20 интегральных микросхем (ИМС), заключенных в керамические корпуса (рис. 2). ЭС находится в условиях свободного конвективного теплообмена с воздушной средой при нормальном давлении. Моделирование интервально стохастического температурного поля ЭС проводилось в условиях интервальной неопределенности, ±10 %-м разбросе мощностей потребления ИМС, тепловых сопротивлений корпусов ИМС и монтажных зазоров.
Результаты моделирования показывают, что реальные значения температуры не являются однозначно определенными и являются интервальными, причем разброс реальных температур ИМС может достигать ±15,6 %.
Заключение
Разработанный метод моделирования температурных полей ТС в условиях интервальной неопределенности исходных данных, адекватно описывает реальную практику. Применяемый в настоящее время детерминированный подход при моделировании температурных полей ТС не адекватен реальным данным, имеющим место на практике. Отметим, что попытки моделировать неопределенности с использованием интервальной арифметики [8] приводят к неоправданно широким интервалам температур и некорректным результатам, что объясняется зависимостью интервальных операций от последовательности вычислений. Разработанный в статье метод показал свою эффективность при тепловом проектировании различных ЭС.
Работа поддержана грантом РФФИ № 12-07-00076-а.