В данной работе предполагается, что вибрации маятника из однородного стержня происходят в точке подвеса вдоль горизонтали. Рассмотрим систему, состоящую из тонкого однородного стержня, вращающегося вокруг горизонтальной оси O1z1 в поле тяжести. Конец О1 стержня является точкой подвеса системы. Предполагается, что точка О1 совершает гармонические колебания вдоль горизонтали по закону y = a cos ωt относительно некоторой фиксированной точки О. Пусть m – масса стержня, а l – его длина. Угол отклонения стержня от вертикального положения обозначим через φ. Момент инерции стержня относительно оси вращения О1 равен I = ml2/3. Определим кинетическую энергию тела, если ось подвеса перемещается горизонтально со скоростью 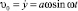 .
.
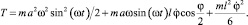
Потенциальная энергия системы П, вычисляется по формуле:
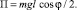
Перейдем к составлению уравнения Лагранжа, которое для данной задачи имеет вид:
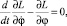
где L = T – П.
После подстановки производных в уравнение Лагранжа и его упрощения получим дифференциальное уравнения движения стержня с вибрирующим подвесом:
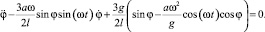
Результаты численного решения при ω = 20 с–1, а = 0,005 м, l = 0,06 м и начальных значениях
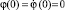
по амплитуде, согласуются с экспериментальными значениями вибромаятника.

