Специалисту любого профиля в современных условиях необходимы глубокие математические знания для решения задач, возникающих в профессиональной деятельности. Особая роль при этом отводится дифференциальным уравнениям, которые позволяют моделировать разнообразные физические, технические, социально-экономические процессы и явления.
Дифференциальные уравнения составляют один из основных разделов высшей математики, через который она реализует себя в практических задачах.
Дифференциальные уравнения уникальные по содержанию и универсальные по применению средства познания мира. Дифференциальные уравнения содействуют более объективному пониманию того или иного явления, эффективному их использованию и повышают достоверность получаемых результатов.
Задачами, приводящими к дифференциальным уравнениям, ученые начали заниматься в начале XVII века. Дж. Непер занимался созданием логарифмической таблицы, Г. Галилей изучал движения твердого тела в среде без сопротивления, Р. Декарт исследовал плоскую кривую на основе свойств ее касательных. Все они пришли к простейшим дифференциальным уравнениям первого порядка с разделяющимися переменными.
Систематическое обращение к дифференциальным уравнениям, как к инструменту исследования различных задач, начинается в середине XVII века, после гениальных работ И. Ньютона и Г.В. Лейбница по созданию дифференциального и интегрального исчислений.
Первоначально теория дифференциальных уравнений развивалась внутри математического анализа. Лишь постепенно, по мере выяснения особенностей ее проблем и установления ее центральных понятий, выделилась в особую математическую науку. Термин «дифференциальное уравнение» ввел в употребление Лейбниц.
Математический анализ полнокровно реализует себя в прикладных задачах через дифференциальные уравнения. Это и закономерно, так как производная функции определяет такие практические понятия, как угловой коэффициент касательной к кривой, мгновенную скорость движения, силу тока в электрической цепи и т.д. Вторая производная дает возможность определить кривизну кривой, ускорение, движение тока в цепи и т.д. Дифференциальные уравнения связывают искомую функцию, ее производные различных порядков и независимые переменные. Дифференциальные уравнения являются, несомненно, важнейшим математическим аппаратом при моделировании процессов, происходящих в природе и обществе.
Модель является представлением объекта в некоторой форме, отличной от формы его реального существования. Математическая модель выражает существенные черты объекта или процесса языком уравнений и других математических средств.
В профильных математических классах учащимся целесообразно предложить элективный курс «Дифференциальные уравнения». Приведем примеры задач из математики, механики, физики, приводящие к дифференциальным уравнениям, которые целесообразно рассмотреть с учащимися.
Задача 1. Найти кривые, отрезок любой касательной к которым, заключенной между осями координат, делится пополам в точке касания.
Решение задачи приводит к дифференциальному уравнению 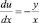 .
.
Задача 2. Найти закон движения точки, движущейся по прямой линии с постоянным ускорением.
Решение задачи приводит к дифференциальному уравнению
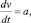
где v – скорость точки; t – время; a – ускорение.
Задача 3. Известно, что скорость радиоактивного распада пропорционально количеству еще не распавшегося вещества. Найти закон распада, если в начальный момент времени t = 0 имелось y0 вещества.
Решение задачи приводит к дифференциальному уравнению
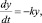
где y(t) – количество вещества, находящегося в наличии в момент t, k > 0 – коэффициент пропорциональности – постоянная распада, знак минус указывает на уменьшение y при увеличении t.
Задача 4. Поглощение светового потока тонким слоем воды пропорционально количеству падающего на него света и толщине слоя. Слой воды толщиной 35 см поглощает половину падающего на него света. Какую часть света поглотит слой воды толщиной в 2 м?
Решение задачи приводит к дифференциальному уравнению
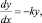
где y(t) – количество света, прошедшего через слой в x, см; k – коэффициент пропорциональности.
Задача 5. Известно, что чем выше над уровнем моря, тем воздух разряженнее – атмосферное давление с высотой уменьшается. Определить зависимость p = p(h) давления от высоты h.
Решение задачи приводит к дифференциальному уравнению
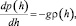
где ρ(h) – плотность воздуха на высоте h; g – ускорение свободного падения.
Задача 6. Пусть в начальный момент тело массой m имеет температуру T0. Температура окружающей среды постоянна и равна Tc, T0 > Tc. Найти закон охлаждения тела.
Решение задачи приводит к дифференциальному уравнению
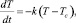
где k – коэффициент пропорциональности.
В нашей работе [1] приведено достаточно большое число задач (физики, теоретической механики, сопротивление материалов, гидравлики, теории машин и механизмов, химии, технологии производства, биологии, экологии, финансово-экономическим дисциплинам и др.), решение которых приводит к дифференциальным уравнениям.
Эти примеры показывают, что дифференциальные уравнения являются действенным математическим аппаратом, через который реализуются основные задачи естествознания.
Элективный курс «Дифференциальные уравнения», рассчитанный на 32 часа, может быть такого содержания.
1. Из истории развития дифференциальных уравнений – 2 часа.
2. Обыкновенные дифференциальные уравнения первого порядка.
2.1. Геометрический способ решения дифференциальных уравнений – 2 часа.
2.2. Дифференциальные уравнения с разделяющимися переменными – 2 часа.
2.3. Обыкновенные дифференциальные уравнения – 2 часа.
2.4. Уравнения, сводящиеся к однородным – 2 часа.
2.5. Линейные дифференциальные уравнения первого порядка – 2 часа.
2.5.1. Метод Лагранжа – 2 часа.
2.5.2. Метод Бернулли – 2 часа.
2.6. Уравнения Бернулли – 2 часа.
2.7. Уравнения в полных дифференциалах – 2 часа.
2.8. Уравнения Лагранжа и Клеро – 2 часа.
3. Дифференциальные уравнения высших порядков.
3.1. Дифференциальные уравнения, допускающие понижение порядка – 2 часа.
3.2. Линейные дифференциальные уравнения высших порядков – 2 часа.
3.3. Линейные однородные дифференциальные уравнения высших порядков с постоянными коэффициентами – 2 часа.
4. Решение дифференциальных уравнений с помощью компьютерных математических пакетов.

