В российской системе образования на старшей ступени общеобразовательной школы реализуется профильное обучение учащихся. Гибкую систему профильного обучения обеспечивает разнообразная комбинация учебных предметов.
Учебные планы включают базовые общеобразовательные предметы, профильные общеобразовательные предметы и элективные курсы, занимающие в учебном плане соответственно 50, 30 и 20 %.
Элективные курсы – средство создания пространства индивидуальной познавательной деятельности учащихся. Являясь вариативной частью профильного обучения, элективные курсы позволяют в большей мере, чем базовые и профильные, построить процесс обучения с учетом способностей, склонностей и потребностей учащихся.
Одной из важнейших задач элективов в условиях профильного обучения является знакомство учащихся со спецификой ведущих для данного профиля видов деятельности, что способствует профильному самоопределению школьников.
Идея элективных курсов в системе профильного обучения предполагает самостоятельное проектирование этих курсов учителем, предоставление учителю больших возможностей в выборе содержания, подборе форм и методов при проектировании и организации элективных курсов.
Элективные курсы могут быть двух типов: предметно-ориентированные и межпредметные. В физико-математическом профиле эффективным будет предметно-ориентированный элективный курс «Решение уравнений высших степеней», рассчитанный на 12 часов.
Его содержание и тематическое планирование могут быть такими:
1. Из истории решения уравнений высших степеней – 2 часа;
2. Решение уравнений третьей степени – 4 часа;
3. Решение уравнений четвертой степени – 4 часа;
4. Решение уравнения Муавра (уравнение пятой степени) – 2 часа.
Рассмотрим содержание некоторых вопросов предложенного элективного курса.
1. Решение уравнений третьей степени.
Общее уравнение третьей степени имеет вид:
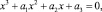
где a1, a2, a3 – произвольно заданные параметры. Его можно свести к уравнению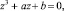 
имеющему более простой вид. Для этого из первых двух слагаемых выделим полный куб:
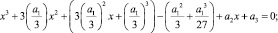
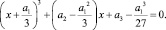
Теперь можно переписать уравнение для переменной z:
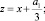
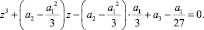
Итак,
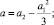
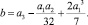
Уравнение примет вид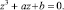 
Его тоже называют общим уравнением третьей степени. Для его решения используют метод Гудде (Гудде Иоганн – голландский математик, 1633-1704), который состоит в представлении переменной z в виде суммы двух частей: z = u + v.
Подставим u + v вместо z в уравнение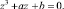 
Будем иметь
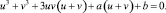
Выберем следующее дополнительное условие: 3uv = –a. Согласно этому условию будем иметь уравнение u3 + v3 = –b.
В итоге имеем систему:
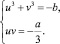
Если возвести в куб второе уравнение системы, то она превращается в систему Виета относительно переменных u3 + v3 для квадратного трехчлена
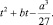
Дискриминант последнего имеет специальное обозначение:
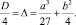
Его неотрицательность означает возможность нахождения корня у общего уравнения третьей степени методом Гудде. Корни этого квадратного трехчлена имеют вид: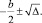 
. Значит,
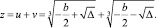
Последняя формула носит название формулы Кардано (Кардано Джероламо – итальянский математик, 1501–1576).
2. Решение общего уравнения четвертой степени.
Общее уравнение четвертой степени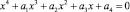 
можно привести к виду 
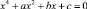, перейдя к переменной 
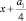. Последнее уравнение также называется общим уравнением четвертой степени.
Для его решения можно использовать метод Гудде, разложение на множители, метод Феррари.
Метод Гудде
Представим корень (удвоенный) в виде трех слагаемых 2x = u + v + w. Умножим обе части уравнения на 16 и подставим последнюю формулу в него:
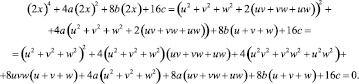
На слагаемые в последней формуле наложим два условия.
Пусть в последней формуле второе и шестое слагаемые в сумме будут равны нулю:
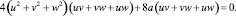
Для этого достаточно наложить условие:
.
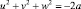Пусть, кроме того, четвертое и седьмое слагаемые в сумме будут равны нулю:
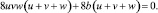
Для этого достаточно наложить условие: uvw = –b.
С учетом наложенных условий перепишем исходное уравнение:
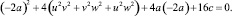
Оно эквивалентно уравнению:
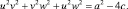
В результате получаем систему:
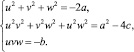
Если последнее уравнение системы возвести в квадрат, то относительно квадратов переменных получится система из теоремы Виета для уравнения третьей степени. Другими словами, уравнение:
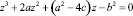
имеет корни: z1 = u2, z2 = v2, z3 = w2.
Для решения общего уравнения четвертой степени нужно решить данное уравнение третьей степени, вычислить квадратные корни из корней этого уравнения и положить: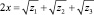 
. Однако таким образом получается восемь решений (знак у каждого из корней можно выбрать двумя способами). Но не все эти решения соответствуют решениям системы и, значит, корням исходного уравнения.
Выберем знаки у квадратных корней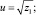 
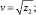
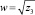таким образом, чтобы выполнялось условие uvw = –b.
Это условие будет выполняться, если одновременно у двух корней изменить знак на противоположный. В итоге получаем все четыре корня общего уравнения четвертой степени:
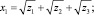
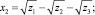
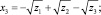
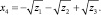
Разложение на множители.
Разложим левую часть общего уравнения четвертой степени в произведение двух квадратных трехчленов с неопределенными коэффициентами:
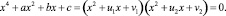
Если нам удастся выразить u1, u2, v1, v2 через коэффициенты исходного уравнения, то мы легко найдем все его корни, решив два квадратных уравнения.
Раскрывая скобки, мы получим уравнение:
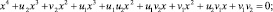
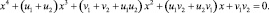
Приравняем коэффициенты при одинаковых степенях. Получим систему уравнений:
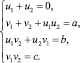
Первое и последнее уравнения системы дают возможность избавиться от двух переменных: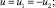 
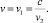В результате получаем систему двух уравнений с двумя неизвестными:
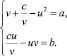
Выберем такие переменные t1 и t2, чтобы u2 = t1t2,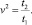 
Для этого достаточно положить
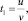t2 = uv.
Тогда первое уравнение системы перепишется в виде
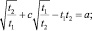
второе уравнение системы перепишется в виде t2 = ct1 – b.
Умножив обе часть первого уравнения на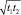 
, можно переписать его в виде
.
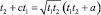Теперь подставим в него t2 из второго уравнения и возведем обе части в квадрат:
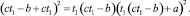
Здесь удобно перейти к переменной t = 2ct1 – b и умножить обе части на 64c3. Тогда уравнение перепишется в виде:
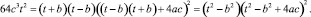
Удобно ввести новую переменную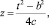 
тогда уравнение перепишется в виде:
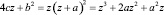
(мы предварительно разделили обе части уравнения на 64c3).
Мы получим точно такое же вспомогательное кубическое уравнение
,
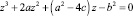что и при решении методом Гудде.
Метод Феррари
Феррари Лудовико – итальянский математик 1522–1565 гг. (ученик Дж. Кардано).
Идея этого метода состоит в том, чтобы представить левую часть общего уравнения четвертой степени в виде разности квадратов.
Она близка к идее предыдущего метода, так как из разности квадратов возникает разложение в произведение двух квадратных трехчленов.
Подберем такой параметр t, чтобы следующее выражение представляло собой разность квадрата квадратного трехчлена и квадратного линейного выражения:
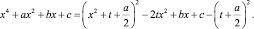
Для этого необходимо и достаточно, чтобы дискриминант квадратного трехчлена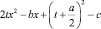 
равнялся нулю.
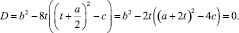
Положив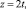 
получим прежнее вспомогательное уравнение:
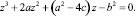
Замечание. Все три метода приводят к одному и тому же вспомогательному кубическому уравнению. Это наводит на мысль, что общее уравнение четвертой степени решается по существу только одним методом, хотя и возможны различные подходы.
Некоторые доводы в подтверждение этой мысли читатель найдет в книге [3].
3. Уравнение Муавра
Муавр Абрахан де – английский математик 1667–1754 гг.
Уравнение Муавра – это уравнение пятой степени, имеющее вид:
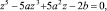
где a и b – параметры.
Решим это уравнение методом Гудде.
Подставим в уравнение
z = u + v.
Будем иметь:
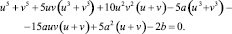
Внешний вид слагаемых, имеющих множитель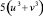 
, приводит к идее выбрать в качестве дополнительного условия уравнение uv – a = 0. Это можно увидеть, вынеся за скобки третьего и пятого слагаемых общий множитель 
.
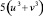Представим шестое слагаемое в виде
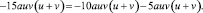
Слагаемое –10auv(u + v) сгруппируем со слагаемым 10u2v2(u + v), вынося за скобки общий множитель, получим:
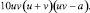
Сгруппируем второе слагаемое –5auv(u + v) со слагаемым 5a2(u + v), вынося за скобку общий множитель, получим:
.
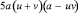Наложим дополнительные условия: обнуляем все слагаемые, кроме выражения u5 + v5 – 2b. В результате получаем систему:
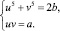
Возведя второе уравнение системы в пятую степень, получим систему Виета относительно переменных u5 и v5 для квадратного трехчлена t2 – 2bt + a5.
Условие неотрицательности дискриминанта есть условие применимости метода Гудде: b2 ≥ a5.
При выполнении этого условия, получаем корень уравнения Муавра:
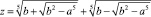
Задачи для самостоятельного решения
1. Решите уравнения:
а)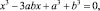 
б)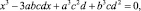 
в)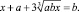 
2. Решите биквадратное уравнение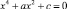 
методом Гудде, разложением на множители, методом Феррари.