Известно, что предмет статистической физики изучает специфические закономерности характерные только для очень большого количества частиц, молекул или атомов. В целом характер движения частиц могут быть описаны классической или квантовой механикой, самое главное чтобы было огромное количество частиц. Если количество частиц будет минимальным, тогда все статистические закономерности теряют свое значение и характер движения частиц будут описываться другой теорией.
Именно вот этот момент должны хорошо усвоить учащийся или студенты, так как сама статистика связана с описанием большого количества элементов. В первую очередь нужно отметить, что при работе с большим количеством частиц описать отдельные характеристики каждого элемента не возможно, тут ни времени, ни материалов не хватит естественно. Во вторых отметим, что формально механические закономерности не могут заменить статистические закономерности.
Самое главное в статистической физике вводятся такие понятия как фазовое пространство, фазовая точка, фазовая траектория,статистическое распределение которые нужно освоить уже на начальном этапе. Здесь и в дальнейшем нужно основательно освоить, что все выводы статистической физики имеют вероятностный характер, а в классической механике мы привыкли к точным, однозначным выводам. После таких рассуждений обучающиеся могут придти к выводу, что статистика – не совсем точно описываемая наука, а приближенная вроятностная наука. Здесь уместно привести примеры того, что законами статистической науки пользуются многие сферы жизни человечества, например социология, производственная сфера, медицина, педагогика и т.д. Например из результатов статистических свойств замкнутых систем, мы можем определить средние значения любых физических величин. Отсюда получаем фундаментальные законы природы – законы сохранения энергии, импульса и момента импульса. Таким образом мы получаем для замкнутой системы функцию распределения, а это является самой главной характеристикой статистической физики.
Для детального понимания роли статистических закономерностей и флуктуационных явлений постараемся обьяснить значение диалектического понимания роли статистических законов в науке.Известно, что все события происходящиеся в микромире описываются с помощью волновой функции (пси функции), которая сама по себе не имеет физического смысла, физический смысл имеет квадрат волновой функции – определяющий вероятность нахождения частицы в определенном обьеме, а математическим аппаратом квантовой механики являются статистические (вероятностные) закономерности. Здесь конечно у всех сразу возникает вопрос насколько статистические закономерности соответствуют истинным величинам, неужели законы микромира описываются теорией вероятностей.
В принципе наука рассматривает два основных типа причинно – следственных связей и соответственно два типа закономерностей – динамические и статистические (вероятностные). Первое позволяет делать предсказания абсолютно жесткие, однозначные, а вторые – вероятностные. После того как в середине девятнадцатого века вероятность стала использоваться в физике, возник вопрос о соотношении между динамическими и статистическими закономерностями.
Первоначально данный вопрос решался в пользу примата динамических закономерностей. Считалось, что статистические законы обусловлены неполнотой наших знаний, что к вероятностному описанию приходится прибегать, когда неизвестны детали картины, когда трудно или нельзя точно учесть все данные, все взаимодействия. Такую концепцию называют концепцией неполноты знаний или, лучше, концепцией преимущества динамических законов. Фактически она предполагала, что за статистическими законами обязательно «скрываются» динамические, что в основе всего лежат именно динамические законы. Известно, что в начале двадцатого века когда формировалась физическая теория процессов микромира великий датский физик Нильс Бор воскликнул неужели Бог с нами играет в кости? В данное время известно, что вероятностное поведение присуще не только большому коллективу, но и отдельным молекулам и атомам, фактически вероятностное описание показывает поведение атома или молекулы на более глубоком уровне. В настоящее время поиск «скрытых» параметров в квантовой механике фактически прекращен теория микро мира описывается вероятностными закономерностями.
Концепция преимущества динамических закономерностей оказалась весьма живучей. Это обьясняется рядом причин. Во-первых, статистические физические теории возникли позднее динамических и, как казалось, на базе последних. Так, статистическая механика имеет в качестве своего «динамического аналога» классическую механику, а микроскопическая электродинамика – классическую электродинамику. Во-вторых, представлялось ( да и сегодня представляется функции), что однозначные предсказания, получаемые в динамических теориях, в большей мере, чем, вероятностные, отвечают самому духу «точной науки». Во –первых, для понимания принципиальной роли статистических законов требуется владение диалектикой, рассмотрение таких диалектических категорий, как необходимое и случайное, возможное и действительное. Именно недиалектическое понимание этих категорий и есть та основная, на наш взгляд, причина, которая обьясняет принижение и даже отрицание принципиальной роли статистических законов.
В этой связи отметим так называемую концепцию равноправия, она показывает, что динамические и статистические закономерности в определенном смысле равноправны – они играют одинаково важную роль, но в разных областях, законы поведения индивидуальных обьектов динамические, а законы поведения больших коллективов статистические. Согласно такой концепции, при переходе, например, от изучения движения отдельной молекулы к изучению газа динамические законы должны переходить в статистические. В данное время такая концепция представляется неправомерной. Серьезный удар по этой концепции нанесла квантовая механика, показавшая, что для проявления статистических закономерностей необязательно наличие коллектива обьектов – даже отдельный обьект может описываться этими закономерностями. Например в микромире если мы наблюдаем дифракционную картину потока электронов, такую же дифракцию можно наблюдать и от отдельных электронов. Согласно неопределенности Гейзенберга состояние электрона в микромире характеризуется неопределенностью координаты и неопределенностью импульса, электрон локализован в определенном интервале.
Рассматривая проблему соотношения между динамическими и статистическими закономерностями, современная наука исходит из концепции преимущества статистических закономерностей. Не только динамические, но и статистические законы выражают обьективные причинно – следственные связи. Более того, именно статистические закономерности являются фундаментальными, по сравнению с динамическими закономерностями они глубже выражают указанные связи. Современную концепцию можно сформулировать так: «Динамические законы представляют собой первый, низший этап в процессе познания окружающего нас мира, статистические законы более совершенно отображают обьективные связи в природе, они являются следующим, более высоким этапом познания».
Теперь все сказанное выше попробуем доказать аргументированно. Постепенно от динамических теории осуществился переход к статистическим теориям. Все фундаментальные физические теории можно разделить на группы – динамические и статистические теории.
К динамическим теориям относятся классическая механика, механика сплошных сред (гидродинамика), теория упругости, феноменологическая термодинамика, классическая электродинамика (включая волновую оптику), специальная и общая теория относительности ( начало двадцатого века).
Все эти теории возникли на рубеже с семнадцатого и в начале двадцатого веков, в этих теориях состояние физического обьекта (системы) однозначно определяется заданием точных значений тех или иных величин. Почти все фундаментальные динамические теории были созданы на рубеже 18–20 веков, с ними связано становление физики как науки, охватывающей широкий круг явлений – механических, тепловых, электрических, магнитных, оптических. Из динамических теорий лишь теория относительности создана в двадцатом веке. После ее создания в самом начале века победное шествие динамических теорий прекратилось – с тех пор новых динамических теорий не появилось. «Теория гравитаций Эйнштейна – это последний триумф динамических закономерностей».
Со статистической теорией получается совсем другая картина. Впервые вероятность была использована в физике в середине девятнадцатого века (теория Максвелла). Именно тогда и появились впервые термины динамическая теория и статистическая теория.
Первая статистическая физическая теория – статистическая механика – возникла во второй половине девятнадцатого века на основе фундаментальных работ Максвелла и Больцмана. Вскоре обнаружилось, что применение этой теории к тепловым процессам позволяет обьяснить важнейшие положения феноменологической термодинамики и прежде всего второе начало термодинамики. Тем не менее статистическая механика с большим трудом завоевывала сторонников – слишком сильна была всеобщая приверженность к «точным» динамическим теориям [1–3].
Итак, даже самый общий взгляд на историю возникновения фундаментальных физических теорий позволяет сделать вывод, что динамические теории соответствовали первому этапу в процессе познания природы человеком, тогда как на следующем этапе главную роль стали играть статистические теории. Уже отсюда видно, что вероятностные закономерности являются более глубокими, более фундаментальными по сравнению с динамическими и что попытки искать «скрывающиеся» за статистическими законами однозначные связи заведомо обречены на неудачу.
Теперь рассмотрим решение многих задач статистической физики и термодинамики, где имеют место применения различные законы распределения.
В применении к молекулам газа распределение Гиббса выглядит следующим образом:
;
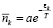а – постоянная
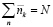
N – полное число частиц в газах.
Это распределение Максвелла, распределение Больцмана, Гиббса, распределение вероятностей для осциллятора, распределение Ферми-Дирака, распределение Бозе-Эйнштейна и т.д. Здесь конечно одними динамическими теориями не обойтись, так как систему многих частиц нужно рассматривать детально, надо учитывать для многих частиц спины частиц, функции распределения, волновые функции и т.д. Вообще говоря в принципе в квантовом случае вероятность различных значений координаты осциллятора отличается от функции классического рапределения, но в предельном случае оно переходит в классическое распределение. Это уже говорит о том, что квантовое распределение вероятности различных значений координаты осциллятора- является более глубокой теорией. Например в СТО А. Эйнштейна преобразования Лоренца в частном случае переходят в преобразования Г. Галилея, что показывает фундаментальность Лоренцовых преобразований.
Для системы многих частиц в квантовой механике распределения отличаются в зависимости от спина, волновой функции и т.д., так как для классических частиц раньше мы не сталкивались с таким понятием как спин, спин-это чисто квантомеханическая характеристика микрочастицы. Например для идеального газа если температура достаточно низкая, то тогда статистика Больцмана становится неприменимой и должна будет построена другая статистика. Для частиц с полуцелым спином, будет применена антисимметричная функция распределения, т.е. для фермионов будет распределение Ферми-Дирака.
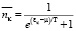
Это распределение идеального газа подчиняющегося статистике Ферми-Дирака, при условии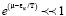 
оно переходит в распределение Больцмана.
Распределение Ферми нормирована следующими условиями:
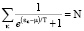
где N – полное число частиц в газах. Это равенство химический потенциал в неявном виде.
Термодинамический потенциал определяется следующим соотношением:
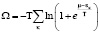
Для частиц с целым спином, будет применена симметричная функция распределения, т.е. для бозонов будет распределение Бозе-Эйнштейна.
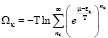
Здесь геометрическая прогрессия выполняется при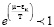 
значениях.
Таким образом химический потенциал в статистике Бозе-Эйнштейна всегда будет отрицательным. В распределении Ферми-Дирака химический потенциал может быть быть и отрицательным, и положительным.
Термодинамический потенциал определяется следующим соотношением:
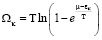
Отсюда находим полное число частиц:
:
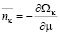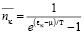
Это распределение идеального газа подчиняющегося статистике Бозе-Эйнштейна.
Для фермионов выполняется так называемый принцип Паули,в каждом квантовом состоянии может находиться одновременно не более одной частицы. Функция распределения для идеального газа, которая подчиняется статистике Ферми в частном случае переходит в функцию распределения Больцмана. В квантовой статистике разные распределения отличаются также в зависимости от химического потенциала.
Подводя итоги можно сказать, что квантовые статистические распределения исследуют состояния микрообьектов более глубже и досконально, это следующий этап изучения законов микромира, более высокий этап познания законов природы.