В работах [1, 2] была обоснована необходимость разработки математических моделей интегрального показателя (ип) здоровья населения и описана одна из таких моделей. Модель использует в качестве параметров 5 показателей здоровья (пз) из государственной статистики, публикуемой ежегодно Госкомстатом рф:

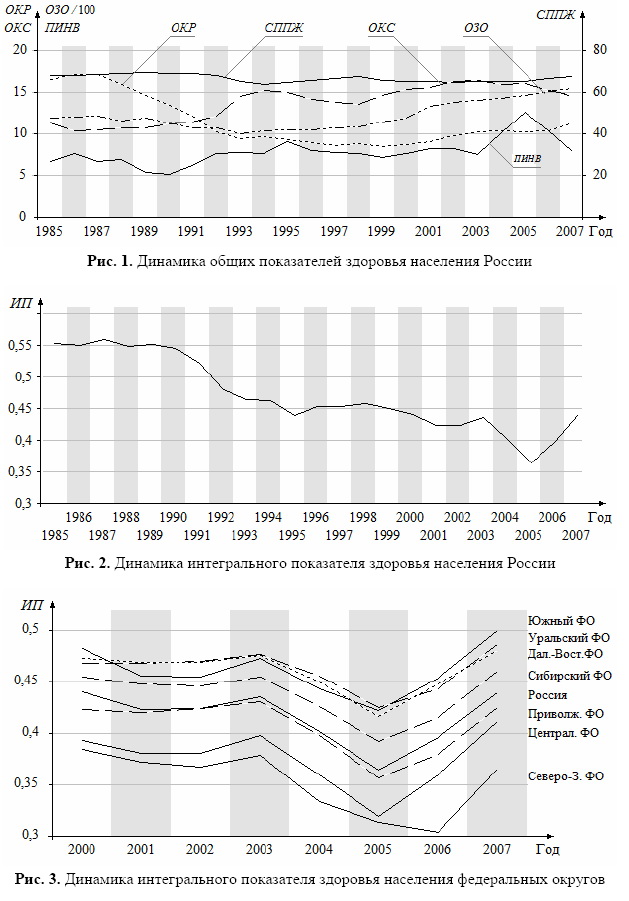
В приведённой модели ОКР - общий коэффициент рождаемости, сппж -средняя продолжительность предстоящей жизни (при рождении), ОЗО - общая заболеваемость по обращениям населения в учреждения здравоохранения, ОКС - общий коэффициент смертности, ПИВН -первичная инвалидность. Определяемые согласно этой модели значения ИП не выходят за пределы промежутка [0, 1]. Значения весовых коэффициентов параметров модели определены с помощью методики, предложенной в [3 - 5].
Отметим, что поскольку значениями параметров разработанных моделей являются фактически полученные значения показателей здоровья, то они отражают и влияние на них различных социально-экономических и природных условий жизни.
На основе предложенной модели было проведено исследование динамики ип здоровья населения России в целом и её федеральных округов. Ниже приводятся результаты этого исследования.
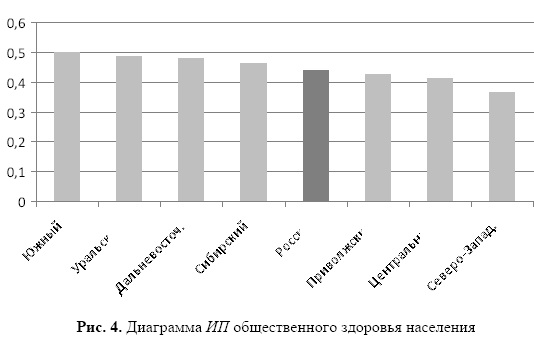
Согласно результатам исследования в перестроечные и послеперестроечные годы наиболее интенсивно падала рождаемость и возрастала смертность. Возрастали также заболеваемость и инвалидность, падало расчётное значение средней продолжительности предстоящей жизни (при рождении). Соответственно уменьшалось и значение ип здоровья населения (рис. 1 - 3).
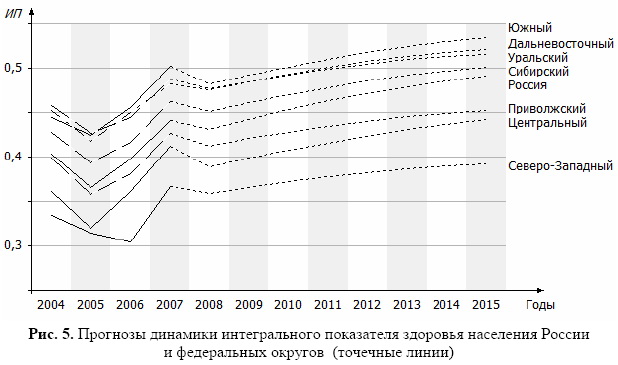
Заметное увеличение ип здоровья населения началось в среднем с 2006-го года. По федеральным округам в 2007-м году значение этого показателя оказалось уже на уровне 2000-го года (рис. 3, 4).
Автором были также исследованы различные алгоритмы прогнозирования для использования их при прогнозировании ИП здоровья населения. Анализ точности алгоритмов прогнозирования проводился путём прогнозирования показателей здоровья на годы, в которые они уже были известны. В результате определялось среднее значение абсолютной погрешности прогнозирования. Исходя из динамики изменения указанных показателей за последние годы и требования уменьшения погрешности прогнозирования для прогнозирования была выбрана следующая линейная модель, учитывающая значения показателей здоровья в последние 4 года:
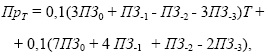
где Прт - значение прогноза рассматриваемого ПЗ, в том числе и ИП, на шаге T (через T лет), а индексы у ПЗ указывают значение шага (года) прогнозирования, когда последний год считается нулевым.
С помощью приведённой модели предстоящей динамики изменения ПЗ населения были определены соответствующие прогнозы на 2008 - 2015 годы (публикация значений всех необходимых
ПЗ населения за 2008-й год ГОСКОМСТАТом РФ ожидается не ранее конца 2009-го года). Для удержания получаемых прогнозов в промежутке [0, 1] они умножались ещё на коэффициенты, изменяющиеся по экспоненциальному закону. Результаты прогнозирования приведены на рис. 5.
Вывод: полученные результаты свидетельствуют о том, что после многолетнего ухудшения показателей здоровья населения, обусловленного сложными социально-экономическими условиями жизни в перестроечные и послеперестроечные годы, можно ожидать медленного улучшения этих показателей.
СПИСОК ЛИТЕРАТУРЫ:
1. Кирьянов Б.Ф., Медик В.А. Усовершенствованные многопараметрические модели интегрального показателя общественного здоровья населения / Охрана здоровья населения - национальный приоритет государственной политики (Сборник научных трудов ННЦ Северо-
Западного Отделения РАМН, Том 5) - М.: Медицина, 2006 - С. 67 - 73.
2. Кирьянов Б. Ф. Математические модели интегрального показателя здоровья населения. - М.: Фундаментальные исследования, 2008, № 9. - С. 99 - 100.
3. Кирьянов Б. Ф. Методика определения значений параметров моделей интегрального показателя общественного здоровья / Охрана здоровья населения - национальный приоритет государственной политики (Сборник научных трудов ННЦ Северо-Западного Отделения РАМН, Том 5) - М.: Медицина, 2006. - С. 125 - 130.
4. Кирьянов Б. Ф. К проблеме определения весовых коэффициентов параметров линейных моделей интегральных показателей качества систем / Вестник НовГУ, 2007, № 44. - С. 33 -37.
5. Кирьянов Б. Ф., Кирьянов Д. В. К теории построения интегральных показателей качества систем на основе линейных математических моделей. - М.: Современные наукоёмкие технологии, 2008, № 4. - С. 73 - 74.

