Так как расчет часов по высшей математике для бакалавров нематематического профиля дается мало, все же мы стараемся дать больше. По этому принципу каждый педагог старается каждый год набор своего инструментария выполнить, вот мы и постарались модернизировать технологическую карту академика В. М. Монахова а, который состоит из 4 пунктов на 6. Спросите, по какому принципу?
Во-первых: за 15 часов лекции педагог никак не может рассказать бакалаврам все о высшей математике и для этого мы ввели в модернизированной технологической карте «Семинарские занятия по типичным ошибкам» оно делиться на два пункта:
1) дополнительная микроцель – которая дается для самостоятельного изучения и конспектирования. Оно дается для того что педагог за 15 часов лекции не успевает охватить весь материал.
2) консультативно-коррекционная работа – которая дает бакалавру консультироваться с педагогом в любое время и с помощью педагога исправить все свои минусы.
Во-вторых: в данное время Европа, Азия и многие другие перенимают опыт с запада, и стараются перевести структуру образования под запад и одним словом все переходят на Болонский процесс обучения. А модернизированная технологическая карта дает возможность линейную структуру обучения перестроить под Болонский процесс, то есть перевести под кредитную технологию. И еще оно дает возможность управлять успеваемость бакалавра. Дает возможность измерить ключевую компетенцию будущего специалиста нематематического профиля. Не только педагогу, но и родителям и самому бакалавру.
В-третьих: Стратегической целью современного образования Россией, является повышение качества образования, которое и есть совокупность образовательных результатов, обеспеченных возможностью самостоятельного решения обучающимися значимых для него проблем (коммуникационных, информационных, познавательных, аксиологических, социальных и т.д.). Для этого в последнее время внедряют термины как ключевая компетентность выпускника и компетентностной подход при условий компетентностно-контекстного формата обучения. Опять же появляется вопрос: «Зачем? И почему?»
Так как в данное время рынок труда все больше требует компетентостного специалиста, который во всех различных ситуациях возникающей на любом поприще высококвалифицированный и высококомпетентный специалист должен выдержать достойно и хладнокровно. На основе всех запросов решили на основе компетентостного подхода готовить компетентностных специалистов, и для этого надо измерить ключевые компетентности специалиста. А модернизированная технологическая карта академика В.М. Монахова дает возможность измерить все ключевые компетентности будущего выпускника.
|
Тема №2: «Векторная алгебра» Логическая структура |
|||||
|
Целеполагание |
Диагностика |
Консультативно-коррекционная работа |
|||
|
1 |
2 |
3 |
|||
|
В1: Уметь применять линейные операций над векторами с помощью определения и его свойств |
Д1: Вершины треугольника находятся в точках А (2; 1), В (-1; -2) и С (3;1). Найти длину высоты, проведенной из точки А. 2) Найти скалярное произведение двух векторов: а = (2 , -4 , 1 , 7) b = (6 , -12 , -3 , 15)
Найти длину вектора
4) Дан треугольник АВС. На стороне ВС расположена точка М так, что . Найти |
КК1: Вычислить площадь треугольника с вершинами А(2, 2, 2), В(4, 0, 3), С(0, 1, 0).
|
|||
|
В2: Уметь разложить вектор на координатной оси |
Д2:
1) Заданы начало А (3; 2;-1) и конец В (1; 5; 2) вектора
2) Найти единичный вектор для вектора
4) Даны точки А (1; 2;-1) и В (4; -3; 2). Найти проекции вектора |
КК2: |
|||
|
В3: Уметь производить скалярное и смешанное произведение двух и более векторов |
Д3:
1) Найти скалярное произведение векторов
2) Вычислить объем тетраэдра с вершинами в точкахA1(1; 3; 6), А2(2; 2; 1), А3(-1; 0; 1), А4(-4; 6; -3).
3) Найти смешанное произведение векторов в < |
КК3: |
|||
|
Семинарские занятия по типичным ошибкам |
|||||
|
b1: Уметь суммировать (вычитать) и умножать вектора между собой два и более вектора. |
k1:
1) Найти сумму векторов 4) Дан треугольник с вершинами A(7; 7), В(4; 3), С(3; 4). Найти периметр треугольника. |
||||
|
b2: Критерии коллинеарности и компланарности |
k2:
1) При каком значении mвекторы
2) Найти координаты вектора
3) Пусть
4) Найти координаты вектора , если он коллинеарен вектору |
||||
|
1 |
2 |
3 |
|||
|
b3: Уметь производить скалярное и смешанное произведение над векторами |
k3:
1) Найти скалярное произведение векторов 2) Вычислить объем тетраэдра с вершинами в точкахA1(1; 3; 6), А2(2; 2; 1), А3(-1; 0; 1), А4(-4; 6; -3)Найти внутренний угол при вершине С треугольника АВС, если А(-1; -2; 4), В(3; 2; -2), С(3; -2; 1).
3) Найти смешанное произведение векторов в |
||||
|
Дозирование |
|||||
|
Стандарт |
Хорошо |
Отлично |
|||
Вот мы изъяснили, по какой причине модернизировали технологическую карту академика В.М. Монахова который в течений многих лет пользуется огромным спросом.
Традиционное обучение и внедрение технологической карты в образование очень огромны. К примеру, в традиционной системе все темы в государственном образовательном стандарте сложены в кучку, там не только бакалавр, но и педагог ногу сломит. А в технологической карте все систематизировано, приведено в определенный порядок, там все разъяснено, что и бакалавру и его родителям вся внятно и понятно. Все темы составлены в последовательном порядке, у каждой темы своя логическая структура, микроцель, диагностика, дозирование, консультативно-коррекционная работа, семинарские занятия по типичным ошибкам, дополнительная мкроцель, коррекция. Если по какой либо причине бакалавр отсутствует на занятии, то он самостоятельно по модернизированной технологической карте сможет разобраться в теме или же придти к педагогу на консультативно –коррекционную работу.
Технологическая карта удобна и тем что, в случае отсутствия по той или иной причине преподавателя математики, любой другой педагог может заменить его. Технологическая карта позволяет самореализоваться педагогу и бакалавру одновременно. Технологическая карта дает возможность компетентностного специалиста требуемой государственного образовательного стандарта и рынка труда. Оно дает возможность видеть все плюсы и минусы хода урока, и сформулировать правильный ход действия педагога. Технологическая карта позволить измерить все ключевые компетенции, которые требует в данное время государственного образовательного стандарта. Технологическая карта упрощает работу педагога, позволяющий которому реализовать все планы. Приведены в таблице.
В соответствии с требованиями государственного образовательного стандарта составлена система из трех микроцелей. При изучении данной темы число этих микроцелей оптимально. Все требования государственных образовательных стандартов ими охвачены, что явно представлено в таблице. Так, например, микроцель В2 «Уметь производить основные операции над матрицами» соответствует следующим требованиям Государственного образовательного стандарта: «Уметь вычислять матрицы и выполнять действия над ними; Применять полученные знания и умения в практической деятельности и повседневной жизни: переводить условия реальных задач на математический язык, использовать аппарат алгебры (выражения, правила и свойства) для исследования несложной практической ситуации; записывать условия различных задач на языке математических моделей». А требование государственного образовательного стандарта: «Уметь решать системы линейных уравнений», соответствует двум микроцелям: В4 «Уметь отличать систему линейных уравнений от уравнении других видов» и В6 «Уметь решать системы линейных уравнений». По тому же принципу составлены и другие микроцели. Важно отметить, что согласно требованиям государственного образовательного стандарта необходимо овладеть определенной терминологией. Любая микро цель предполагает знания этой терминологии. Для проверки достижения микроцели составляется система упражнении. Она состоит из четырех заданий. Два первых задания абсолютно просты. Выполнение этих заданий гарантировано выводит студента на стандарт. Два других задания – это задания повышенного уровня сложности. Выполнение этих заданий требует у бакалавра повышенного внимания и сообразительности.
Подготовить бакалавра к успешному прохождению диагностики обязана система упражнений, представленная в четвертой колонке таблицы. Эта система трехуровневая. Первый уровень – это номера, которые готовят учащегося к прохождению диагностики и последующему получению оценки «удовлетворительно». Второй уровень предполагает прохождение диагностики и получение оценки «хорошо». Третий уровень – оценки «отлично».
Удачное прохождение диагностики свидетельствует о том, что математические понятия у бакалавра сформированы на уровне требований государственного образовательного стандарта.


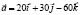 его направляющие косинусы.
его направляющие косинусы.
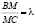
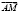 , если
, если 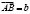 ,
, 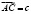
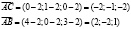
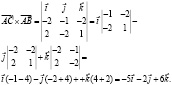
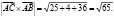
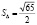 .
.
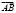 Найти разложение вектора
Найти разложение вектора 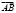 по координатным осям, его модуль и направляющие косинусы.
по координатным осям, его модуль и направляющие косинусы.
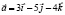 )Найти длину вектора
)Найти длину вектора 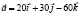 его направляющие косинусы.
его направляющие косинусы.
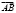 на ось, составляющую с координатными осями равные острые углы.
на ось, составляющую с координатными осями равные острые углы.
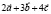 и
и 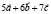 , если
, если
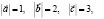
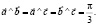
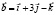 ,,) Вычислить площадь треугольника с вершинами A(1; 1; 1), В(2; 3; 4), С(4; 3; 2)
,,) Вычислить площадь треугольника с вершинами A(1; 1; 1), В(2; 3; 4), С(4; 3; 2)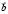
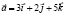
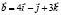
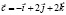 ) Найти разность векторов:
) Найти разность векторов: 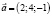 ) Определеить координаты вектора
) Определеить координаты вектора 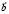 если известно, что
если известно, что 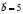 он коллинеарен вектору
он коллинеарен вектору 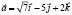 его направление совпадает с направлением вектора
его направление совпадает с направлением вектора 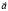
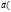 -1;2),
-1;2), 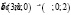 омпланарны?
омпланарны?
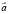 , перпендикулярного векторам
, перпендикулярного векторам 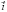 и
и 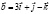 если
если 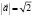
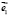 и
и 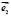 -единичные неколлинеарные векторы. Вычислить
-единичные неколлинеарные векторы. Вычислить 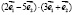 , если
, если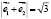
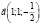 образует острый угол с ортом
образует острый угол с ортом 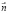 и
и 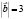
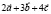 и
и 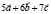 , если
, если 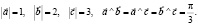
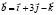 ,,) Вычислить площадь треугольника с вершинами A(1; 1; 1), В(2; 3; 4), С(4; 3; 2)
,,) Вычислить площадь треугольника с вершинами A(1; 1; 1), В(2; 3; 4), С(4; 3; 2)