Для нахождения рабочей площади поперечного сечения спирально-винтового устройства рассмотрим его уравнения двумерной поверхности:
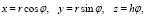
где 0<r<a, 0<φ<2π.
Элемент dS площади имеет вид:
.
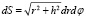Вычисляя интеграл получаем выражение для площади S:
.
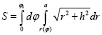Для определения уравнения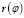 
нижнего предела интегрирования запишем уравнение прямой в отрезках:
,
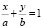где а – внешний радиус винтового устройства;
.
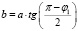Значение угла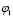 
находится по формуле: 
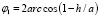. Обозначим 
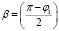и переходя к полярной системе координат 
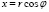, а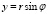 
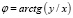, получим:
.
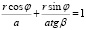Откуда окончательно получаем:
.
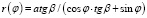Тогда интеграл для вычисления площади поверхности запишется:
.
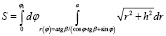При этих данных получается некоторое увеличение пропускной способности из-за конструктивных особенностей спирально-винтовых рабочих органов.