В работе приводится информация о практической реализации метода конечных элементов в перемещениях. Основное внимание уделено оценке точности и достоверности численного решения нестационарных динамических задач. В деформируемом теле при импульсном воздействии возникают возмущения различной природы. Они распространятся с конечными скоростями. Величина возмущений зависит от состояния тела и характера деформаций, в виде волн возмущений, называемых волнами напряжений. При интерференции волн напряжений их интенсивности складываются. Они могут достигать значений, превосходящих предел прочности материала. В этом случае наступает разрушение материала. После трехкратного или четырехкратного прохождения и отражения волн напряжений в теле процесс распространения возмущений становится установившимся, напряжения и деформации усредняются, тело находится в колебательном движении.
Некоторые вопросы в области постановки, разработки методики, алгоритма и достоверности результатов численного моделирования нестационарных динамических задач рассмотрены в следующих работах [3–10].
Разработка методики и алгоритма
Для решения двумерной плоской динамической задачи теории упругости с начальными и граничными условиями – используем метод конечных элементов в перемещениях [3–5, 8–10].
Задача решается методом сквозного счета, без выделения разрывов. Чтобы выполнить динамический расчет методом конечных элементов, нужно иметь матрицу жесткости и матрицу инерции конечного элемента.
Принимая во внимание определение матрицы жесткости, вектора инерции и вектора внешних сил для тела Г, записываем приближенное значение уравнения движения в теории упругости
, 
, 
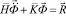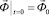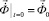, (1)
где: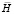 
– матрица инерции; 
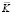– матрица жесткости; 
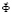– вектор узловых упругих перемещений; 
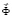– вектор узловых упругих скоростей перемещений; 
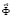– вектор узловых упругих ускорений; 
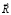– вектор узловых упругих внешних сил.
Соотношение (1) система линейных обыкновенных дифференциальных уравнений второго порядка в перемещениях с начальными условиями. Таким образом, с помощью метода конечных элементов в перемещениях, линейную задачу с начальными и граничными условиями привели к линейной задаче Коши (1).
Для интегрирования уравнения (1) конечноэлементным вариантом метода Галеркина приведем его к следующему виду
, 
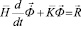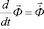. (2)
Интегрируя по временной координате соотношение (2) с помощью конечноэлементного варианта метода Галеркина, получим двумерную явную двухслойную конечноэлементную линейную схему в перемещениях для внутренних и граничных узловых точек
,
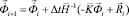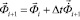. (3)
Основные соотношения метода конечных элементов в перемещениях получены с помощью принципа возможных перемещений и конечноэлементного варианта метода Галеркина.
Система уравнений (1) для внутренних и граничных узловых точек, полученная в результате интегрирования уравнения движения теории упругости, должна давать решение, сходящееся к решению исходной системы.
Шаг по временной переменной Δt определяем из следующего соотношения
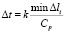
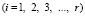, (4)
где: Δl – длина стороны конечного элемента.
Результаты численного эксперимента показали, что при k = 0,5 обеспечивается устойчивость двумерной явной двухслойной конечноэлементной линейной схемы в перемещениях для внутренних и граничных узловых точек на квазирегулярных сетках.
На основе метода конечных элементов в перемещениях разработаны алгоритм и комплекс программ для решения линейных плоских двумерных задач, которые позволяют решать сложные задачи при нестационарных волновых воздействиях на уникальные сооружения.
Решение методических задач
Рассматривается задача о воздействии плоской продольной упругой волны на свободное круглое отверстие. Начальные условия приняты нулевыми.
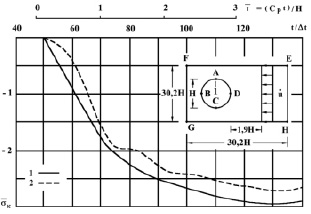
Рис. 1. Изменение упругого контурного напряжения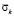 
в точке 1 во времени 
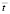на контуре свободного круглого отверстия при воздействии плоской продольной упругой волны типа функции Хевисайда
а)
б)
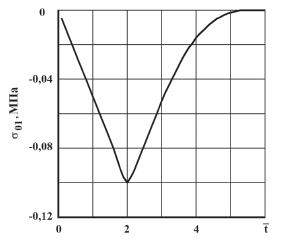
Рис. 2. Экспериментальное воздействие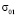 
во времени 
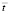, полученное методом динамической фотоупругости: а – фотограмма картин полос; б – экспериментальное воздействие, принятое при численном решении методом конечных элементов в перемещениях
а)
б)
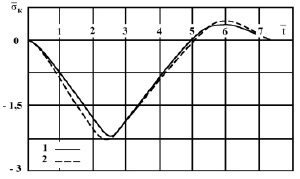
Рис. 3. Изменение упругого контурного напряжения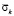 
в точке 1 во времени 
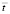на контуре свободного круглого отверстия при воздействии 
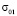: а – фотограмма картин полос; б: 1 – экспериментальные результаты, полученные методом динамической фотоупругости; 2 – результаты численного решения, полученные методом конечных элементов в перемещениях
В сечении на расстоянии 1,9H (рис. 1) при 0 ≤n ≤ 10 (n = t/Δt) скорость упругого перемещения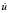 
изменяется линейно от 0 до P (P = σ0/(ρCp) (σ0 = – 0,1 МПа (– 1 кгс/см2)), а при n ≥ 10 
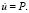Контур круглого отверстия ABCD предполагается свободным от нагрузок при t > 0. Граничные условия для контура EFGH при t > 0 
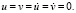Отраженные волны от контура EFGH не доходят до исследуемых точек при 0 ≤ n ≤ 260. Исследуемая расчетная область имеет 1536 узловых точек. Контур круглого отверстия аппроксимирован 28 узловыми точками.
На рис. 1 показано изменение упругого контурного напряжения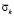 
(
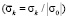в точке 1 во времени 
(
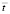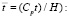1 – результаты аналитического решения [1, 2]; 2 – результаты численного решения, полученные методом конечных элементов в перемещениях [4, 6–8].
Расхождение для максимального упругого контурного напряжения составляет 6 %.
На рис. 2 показано экспериментальное воздействие σ01 во времени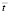 
, полученное методом динамической фотоупругости: а – фотограмма картин полос; б – экспериментальное воздействие, принятое при численном решении методом конечных элементов в перемещениях.
На рис. 3 показано изменение упругого контурного напряжения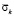 
в точке 1 во времени 
при воздействии σ01: а – фотограмма картин полос; б: 1 – экспериментальные результаты, полученные методом динамической фотоупругости [4, 6–8]; 2 – результаты численного решения, полученные методом конечных элементов в перемещениях [4, 6–8].
Расхождение для максимального упругого контурного напряжения составляет 2 %.
Рассматривается задача о воздействии плоской продольной упругой волны на подкрепленное круглое отверстие.
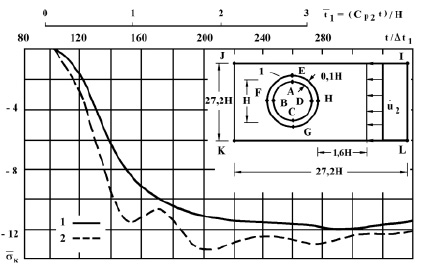
Рис. 4. Изменение упругого контурного напряжения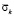 
в точке 1 во времени 
на внутреннем контуре подкрепленного круглого отверстия при воздействии плоской продольной упругой волны типа функции Хевисайда
Начальные условия приняты нулевыми. В сечении на расстоянии 1,6H (рис. 4) при 0 ≤ n1 ≤ 10 (n1 = t/Δt1) скорость упругого перемещения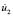 
изменяется линейно от 0 до P1 = σ0/(ρ2Cp2), а при n1 ≥ 10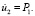 
Внутренний контур подкрепленного отверстия ABCD предполагается свободным от нагрузок при t > 0. На границе подкрепления и среды EFGH приняты условия непрерывности перемещений. Граничные условия для контура IJKL при t > 0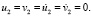 
Отраженные волны от контура IJKL не доходят до исследуемых точек при 0 ≤ n1 ≤ 540 (
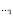– подкрепление; 
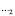– среда). Исследуемая расчетная область имеет 1536 узловых точек. Внутренний контур подкрепления аппроксимирован 28 узловыми точками. По толщине подкрепление аппроксимировано двумя узловыми точками.
На рис. 4 показано изменение контурного напряжения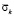 
в точке 1 во времени 
(
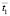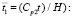1 – результаты аналитического решения [2]; 2 – результаты численного решения, полученные методом конечных элементов в перемещениях [4, 8].
Расхождение для максимального упругого контурного напряжения составляет 12 %.
Выводы
Анализ численных результатов показывает, что метод конечных элементов в перемещениях с успехом применяется для решения нестационарных динамических задач.
Проведенные исследования сходимости и устойчивости, сравнение с результатами других методов показало хорошее совпадение, что позволяет сделать вывод о физической и математической достоверности результатов численного решения динамических задач, полученных методом конечных элементов в перемещениях.
Методика, алгоритм, комплекс программ и результаты решенных задач рекомендуются для использования в научно-технических организациях, специализирующихся в области динамического расчета сооружений с окружающей средой при ударных, взрывных и сейсмических воздействиях.