Длительная прочность древесного стекловолокнистого композиционного материала базового состава, т.е. с заполнителем в виде щепы с длиной элементов 150…200 мм, изучалась на образцах-балках размерами 80´80´700 мм, подвергавшихся изгибающему действию двух сосредоточенных сил, симметрично приложенных в средней трети пролета и погруженных в воду.
Выбор этого варианта древесного композита обусловлен тем, что полученные данные можно было сравнить с результатами исследований на ползучесть аналогичных образцов, но при постоянных температуре и влажности [1].
Испытания проводили на созданном в ВГЛТА рычажном устройстве, которое позволяло создать зону чистого изгиба в средней части образца, где и проводились замеры прогибов индикатором часового типа с ценой деления 0,001 мм. Рычаги устройства позволяли увеличивать прикладываемую нагрузку в 40 раз. Методика установки индикатора и струбцины с площадкой, в которую упирался его шток, размеры пролета П-образной скобы и размеры, определяющие точки приложения нагрузки, были те же, что и при кратковременных испытаниях при проведении эксперимента по определению коэффициента стойкости древесного композита в воде [3], но без длительного приложения постоянной нагрузки.
За счет различных величин грузов устройство позволяло создавать в зоне чистого изгиба образца условные постоянные напряжения, составляющие определенные доли от среднего предела прочности при изгибе, равного 22,0 МПа, а именно нормальные напряжения составили (МПа): 16, 15, 14, 12, 11, 10, 9 и 8. Число образцов в серии для каждой ступени нагружения равнялось трем.
Немедленно после приложения нагрузки в середине зоны чистого изгиба образцов на базе 100 мм (пролет П-образной скобы) измеряли мгновенный, упругий прогиб и подсчитывали мгновенный модуль упругости – 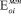 (табл. 1).
(табл. 1).
Далее для построения кривых ползучести (рис. 1) через определенные промежутки времени снимали отсчеты с индикаторов и по величине прогиба подсчитывали секущие модули упругости (деформации) Есек.чи.в(t). В случае разрушения образца фиксировали величину его предела прочности на время t – sсек.чи.в (t). равного sчи.
Таблица 1
Подсчет величин мгновенных модулей упругости древесного композита по величинам прогибов, замерявшихся при установке образцов-балок на исследование процесса ползучести при изгибе
|
Постоянное напряжение – |
Мгновенный упругий прогиб – |
Значение мгновенного
модуля упругости |
|
σ01 = 160 (16) |
0,00510 |
|
|
σ02 = 150 (15) |
0,00480 |
|
|
σ03 = 140 (14) |
0,00450 |
|
|
σ04 = 120 (12) |
0,00385 |
|
|
σ05 = 110 (11) |
0,00350 |
|
|
σ06 = 100 (10) |
0,00320 |
|
|
σ07 = 90 (9) |
0,00290 |
|
|
σ08 =80(8) (теор.) |
0,00265 |
|
|
|
|
|
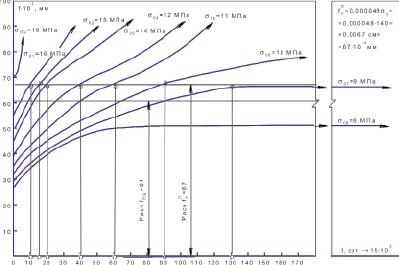
Рис. 1. Кривые ползучести образцов-балок из древесного композиционного материала, помещенных в воду
Конечной целью опытов было определение времени от момента загружения образца до его разрушения или до полного прекращения ползучести; построение кривых зависимости прочности и упругости древесного композита от времени (рис. 2, 3); фиксирование появления на них точек перегиба; получение величины предела длительного сопротивления sчи.в и величины длительного модуля деформации Есек.чи.в (табл. 2), являющихся фиксированными значениями этих величин на 260 сут. экспозиции в воде, а также теоретических значений тех же величин на конец данного срока эксплуатации шпал – 40·365 сут.; получение соответствующих минимальных коэффициентов длительности – Кчи.в и длительного деформационного коэффициента – nчи.в [3, 4].
Ранее Кчи.в и по кривым ползучести определяется лишь приближенно.
Действительно, если имеем кривые затухающей и нарастающей ползучести, то величина длительной прочности будет заключена между величинами постоянных напряжений двух образцов, один из которых разрушается, а другой дает кривую затухающей ползучести [2, 5, 7].
Более точно этот коэффициент может быть получен при построении графика зависимости постоянно действующих напряжений по времени появления на кривых ползучести точек перегиба (по методу, разработанному под руководством В.И. Харчевникова) [6].
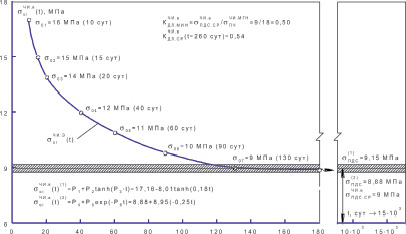
Рис. 2. График зависимости постоянно действующих напряжений при испытаниях образцов-балок из древесного композита, погруженных в воду, на ползучесть при чистом изгибе от времени появления на кривых точек перегиба (к методике определения предела длительного сопротивления)
Таблица 2
Подсчет величин секущих модулей деформаций древесного композита по данным испытаний образцов-балок на момент появления точки перегиба на кривых ползучести при изгибе (расчетная формула:
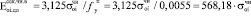 )
)
|
Постоянное напряжение – |
Время достижения полного упругого прогиба – сут |
Значение мгновенного модуля упругости (МПа) |
|
1 |
2 |
3 |
|
σ01 = 160 (16) |
10 |
|
|
σ02 = 150 (15) |
15 |
|
|
σ03 = 140 (14) |
20 |
|
|
σ04 = 120 (12) |
40 |
|
|
σ05 = 110 (11) |
60 |
|
|
σ06 = 100 (10) |
90 |
|
|
σ07 = 90 (9) |
130 |
|
|
σ08 = 80 (8) |
260 |
|
Данный подход использован и для определения величин длительных секущих модулей деформаций (табл. 2, рис. 3), когда, зная фиксированный полный упругий прогиб – fп = 0,0067 см (рис. 1) и величины постоянных напряжений в образцах-балках, можно подсчитать названные модули [3] с помощью коэффициента 3,125, который зависит от размеров поперечного сечения образца, расчетной схемы его нагружения и имеющий ту же размерность, что и прогиб.
С уменьшением величины постоянного напряжения увеличивается время до момента достижения изгибаемым образцом этого прогиба (рис. 1, 2 и 3), а зависимость носит криволинейный характер.
Уточним, что величина fп есть ордината прямой, параллельной оси абсцисс и являющейся геометрическим местом точек перегиба кривых ползучести (рис. 1) образцов из древесного композита при изгибе.
С применением ЭВМ нами были подобраны аппроксимирующие функции, с большой точностью представляющие экспериментальные данные и позволяющие получить значения напряжений, соответствующих пределу длительного сопротивления древесного композита (рис. 2) – 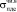 , а также коэффициента длительности –
, а также коэффициента длительности – 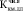 :
:
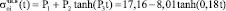 , (1)
, (1)
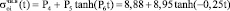 , (2)
, (2)
где Р1 ≅ 17,16 МПа ≅ 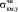 , Р1–Р2 = 17,16 – 8,01 = 9,15 МПа ≅
, Р1–Р2 = 17,16 – 8,01 = 9,15 МПа ≅ 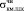 ,
,
Р4 = 8,88 МПа ≅ 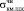 , Р4 + Р5 = 8,88 + 8,95 ≅ 17,83 МПа =
, Р4 + Р5 = 8,88 + 8,95 ≅ 17,83 МПа = 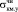 , т.е. эти коэффициенты имеют физический смысл. Р3 = 0,18 и Р6= – 0,25 – релаксационные коэффициенты.
, т.е. эти коэффициенты имеют физический смысл. Р3 = 0,18 и Р6= – 0,25 – релаксационные коэффициенты.
Сумма квадратов отклонений для функции (1) равна 3,725∙10-3 , а для функции (2) – 1,905∙10-3, т.е. с точки зрения точности аппроксимации функция (2) предпочтительнее.
Для подсчета коэффициента длительности использовали среднее значение предела длительного сопротивления
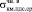 (9,15 + 8,88) / 2 = 9 МПа (рис. 2):
(9,15 + 8,88) / 2 = 9 МПа (рис. 2):
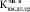 (t = 15∙103 сут.) =
(t = 15∙103 сут.) = 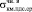 /
/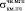 = 9,0/22,0 = 0,41; (3)
= 9,0/22,0 = 0,41; (3)
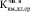 (t = 260 сут.) =
(t = 260 сут.) = 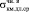 /
/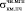 = 9,78/22,0 = 0,45.
= 9,78/22,0 = 0,45.
Аналогичные действия были выполнены и в отношении длительного модуля деформации, а именно: подобраны аппроксимирующие функции, позволяющие вычислить его значение на 260 сутки (время завершения экспозиции в воде) и ожидаемые (теоретические) значения на 40∙365 сутки, т.е. через 40 лет (рис. 3):
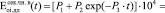
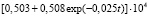 ; (4)
; (4)
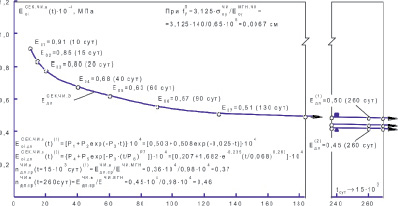 Рис. 3. График зависимости секущих модулей деформации, соответствующих точкам перегиба на кривых ползучести, от времени при испытаниях образцов-балок из древесного композита, погруженных в воду, на чистый изгиб
Рис. 3. График зависимости секущих модулей деформации, соответствующих точкам перегиба на кривых ползучести, от времени при испытаниях образцов-балок из древесного композита, погруженных в воду, на чистый изгиб
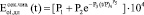
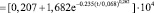 , (5)
, (5)
где 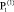 = 0,503∙104 МПа =
= 0,503∙104 МПа = 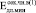 ,
, 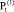 = 0,207∙104 МПа =
= 0,207∙104 МПа = 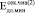 , т.е. и эти коэффициенты имеют физический смысл.
, т.е. и эти коэффициенты имеют физический смысл.
Сумма квадратов отклонений для функции (4) равна 7,213·10-4, для функции (2) – 1,437∙10-4, т.е. с точки зрения точности аппроксимации функция (5) предпочтительнее, хотя трудно предположить, что шпала, например, будет 40 лет находиться в воде, так что полученные значения модулей очевидно занижены.
Как и для коэффициентов длительности подсчитывали среднее минимальное значение длительного секущего модуля деформаций древесного композита – 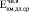 = (0,503 + 0,207)∙104/2 = 0,36∙104 МПа.
= (0,503 + 0,207)∙104/2 = 0,36∙104 МПа.
Длительный деформационный коэффициент – 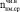 равен:
равен:
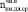 (t = 40·365 сут.)=
(t = 40·365 сут.)= 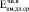 /
/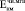 = 0,36∙104/0,98∙104 = 0,37; (6)
= 0,36∙104/0,98∙104 = 0,37; (6)
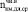 (t = 260 сут.) =
(t = 260 сут.) = 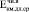 /
/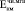 = 0,45∙104/0,98∙104 = 0,46.
= 0,45∙104/0,98∙104 = 0,46.
Приведенные теоретические расчеты значений коэффициентов длительности и длительных деформационных коэффициентов через 40 лет эксплуатации шпал показывают, что в целом соотношения между ними реальные, т.к. значение первого несколько выше, чем второго, т.к. 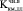 = 0,41 >
= 0,41 > 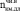 = 0,37. Напомним также, что образцы, исследовавшиеся на ползучесть в воде, не подвергались обработке гидрофобизирующими составами, что, безусловно, создает дополнительные резервы по прочности и жесткости, например железнодорожных шпал различного назначения.
= 0,37. Напомним также, что образцы, исследовавшиеся на ползучесть в воде, не подвергались обработке гидрофобизирующими составами, что, безусловно, создает дополнительные резервы по прочности и жесткости, например железнодорожных шпал различного назначения.


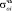 , кгс/см2 (МПа)
, кгс/см2 (МПа)
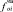 , см
, см
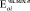 , кг/см2 (МПа)
, кг/см2 (МПа)
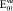 = 0,98∙105(0.98∙104)
= 0,98∙105(0.98∙104)
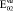 = 0,98∙105(0,98∙104)
= 0,98∙105(0,98∙104)
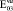 = 0,97∙105(0,97∙104)
= 0,97∙105(0,97∙104)
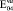 = 0,98∙105(0,98∙104)
= 0,98∙105(0,98∙104)
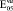 = 0,98∙105(0,98∙104)
= 0,98∙105(0,98∙104)
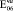 = 0,98∙105(0,98∙104)
= 0,98∙105(0,98∙104)
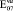 = 0,97∙105(0,97∙104)
= 0,97∙105(0,97∙104)
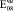 = 0,98∙105(0,98∙104)
= 0,98∙105(0,98∙104)
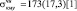
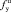 = 0,00550
= 0,00550
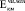 = 0,98∙104 МПа
= 0,98∙104 МПа
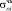 , кгс/см2 (МПа)
, кгс/см2 (МПа)
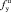 ,
,
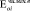 , кгс/см2
, кгс/см2
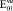 = 0,91·105(0,91·104)
= 0,91·105(0,91·104)
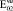 = 0,85·105(0,85·104)
= 0,85·105(0,85·104)
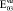 = 0,80·105(0,80·104)
= 0,80·105(0,80·104)
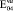 = 0,68·105(0,68·104)
= 0,68·105(0,68·104)
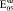 = 0,63·105(0,63·104)
= 0,63·105(0,63·104)
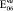 = 0,57·105(0,57·104)
= 0,57·105(0,57·104)
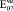 = 0,51·105(0,51·104)
= 0,51·105(0,51·104)
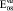 = 0,46·105(0,46·104)
= 0,46·105(0,46·104)