Рассматривая общие принципы решения задач, следует отметить общность между математическим решением задач [1] и логическим принятием решений [2]. По существу, решенная задача является основой принятия решений. Прежде чем принять решение субъект, принимающий решение черпает информацию в информационном поле [3]. Он получает сложную систему параметров, которые нужно проанализировать и редуцировать. На основе параметров он строит информационную модель, которая служит основой для получения решения. При этом возникает противоречие: чем глубже человек вникает в проблему, тем формально лучше и точнее будут принимаемые им решения. С другой стороны, чем глубже человек вникает в проблему, тем больше сложность модели и это влечет ошибки результата. Сталкиваясь с множеством параметров, отражающих сложную ситуацию, человеческий разум объединяет их в группы в соответствии с качественными признаками [4]. В процессе принятия решений человек или живое существо анализирует объекты и отношения между ними. При возникновении сложности человек производит декомпозицию сложного явления или объекта. Фундаментальный процесс, лежащий в основе решения задач, включает в себя декомпозицию и синтез. Хотя проводимые разными людьми декомпозиции могут отличаться одна от другой, лежащий в основе декомпозиции логический метод [5] позволяет получить достаточно близкие оценки ситуации. Особенно это проявляется при необходимости достижения общих целей. Поэтому нужно моделировать действительность таким образом чтобы извлекать общий смысл и исключать индивидуальное.
Основная часть. Задачи первого и второго рода достаточно часто встречаются в человеческой практике и возникают при разных ситуациях: при многоцелевом управлении [6]; при построении виртуальных моделей [7]; при построении и применении когнитивных информационных моделей [8]. Критерием перехода от задач первого рода к задачам второго рода является структурная сложность [9] задачи.
Рассмотрим задачи первого рода. Простейшее принятие решений строится по правилу «Если А, то В». Это означает, что если имеет место информационная ситуация «А», то следует принять действие «В». Такое решение называется простым или однозвенным и описывается одним звеном
А→В. (1)
Такие решающие цепочки имеют место в простых ситуациях, например, при «нормативном» управлении, когда появление ситуации «А» предусмотрено регламентом или нормативом. В таком нормативе предписывается действие «В» для ситуации «А». В этом случае система просто исполняет инструкцию. В биологии цепочка (1) описывает условный рефлекс. В результате действия «В» система переходит в состояние АТ. Топологически это отображается схемой, приведенной на рис. 1.

Рис. 1. Простое однозвенное решение
Точку А называют начальной точкой решения, точку АТ называют конечной точкой или целью решения. Если конечную цель АТ нельзя достичь за одно действие, то имеет место последовательное решение, когда для получения решения требуется цепочка звеньев типа
А1→В1→А2→В2→ ……→ВN-1→АТ (2)
Выражение (2) интерпретируется следующим образов. Информационная ситуация А1 влечет действие В1, которое приводит к информационной ситуации А2. Информационная ситуация А2 влечет действие В2 и так далее, пока не будет достигнуто целевое состояние АТ. Такая цепочка действий называется также «путем решения» или «маршрутом решения». Она служит основой построения последовательного алгоритма, который приводит к решению АТ от исходной ситуации А1. Совокупность действий В характеризует процессы вычислений или принятия решений, если алгоритм связан с решением. Вычисления связаны с компьютерными технологиями, принятие решений относится к живым и интеллектуальным системам.
При наличии системы с памятью возможно улучшение решения. Если цепочки (2) повторяются, то они фиксируются в памяти системы и запоминаются как стереотипные решения. Выражение (2) характеризует сложность решения задач 1 рода, поскольку для получения решения применяется только одна цепочка решающих действий. Возможно наличие группы альтернативных маршрутов решений, например,
D→E→АТ; H→P→ АТ; X→Y→ АТ и т.п.,
Это решения, которые исходят из других начальных точек, но приводят к тому же результату. Однако все они не допускают перехода от одного маршрута к другому. Лицу, принимающему решение, необходимо выбрать оптимальный, по его мнению, маршрут и действовать согласно предписанию этого маршрута. Все это отображается алгоритмом или набором не связанных между собой алгоритмов. Все это характеризует задачи первого рода.
При построении модели, применяемой для решения, она должна отвечать условиям: обозримости, воспринимаемости, понимаемости, интерпретируемости [8]. Если модель отвечает этим условиям, то имеет место задача первого рода.
При невыполнении отмеченных условий возникает сложная ситуация, [10], для которой необходим поиск пути решения, в силу того что возможно много вариантов. Возникает семантический разрыв [11] между потребностями и возможностями человека и его инструментария решения задач первого рода
На рис. 2 показана ситуация, когда из начальной точки Ab возможно множество путей решения. В итоге необходимо получить решение Aо или конечную ситуацию. Такая ситуация является многовариантной. На первом этапе решения необходимо выбрать вариант решения. Он определяет процесс решения и следующее состояние и процесс, который ведет к этому состоянию. Если таких состояний и следующих за ними много, то процесс поиска «пути решения» может стать необозримым [7, 8]. В этом случае сложно или невозможно найти оптимальный путь решения. Эти задачи называют задачами второго рода. Следует отметить, что не много вариантность, а невозможность построения пути решения характеризует задачи второго рода.
Проведем различие между задачами первого рода и задачами второго рода. Задачи первого рода характеризуются однозначностью решения и алгоритмом, который приводит от начальной ситуации к конечной (целевой ситуации). С топологической точки зрения, граф задачи первого рода не имеет циклов.
Задачи второго рода характеризуются неоднозначностью решения и отсутствием единственного алгоритма, который приводит от начальной ситуации к конечной точке. Граф задачи второго рода имеет циклы.
В результате решения задачи второго рода возможны варианты решения. Решение может быть оптимальным Aо. Решение может быть не оптимальным ANO1, ANO1. Решение может быть ошибочным Afalse.
Поэтому для решения задач второго рода необходимо привлечение специальных методов, которые не используют при решении задач первого рода .
Одним из методов решения задач второго рода является так называемый муравьиный алгоритм [12]. Муравьиный алгоритм моделирует алгоритм оптимизации поведения муравьиной колонии (ant colony optimization) при поиске пищи. Он используется для нахождения приближённых решений транспортной задачи, а также для поиска маршрутов на графах. Суть алгоритма заключается в анализе и использовании модели группового поведения отдельных муравьев, ищущих пути от колонии к источнику питания. Первая версия алгоритма, предложенная Марко Дориго [13] была направлена на поиск оптимального пути в графе.
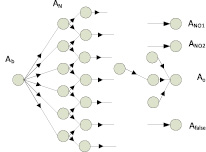
Рис. 2. Граф задачи второго рода
В переводе на информационный язык модель решения ищется с использованием «жадного алгоритма» [14] дополненного возможностью передачи информации от одного агента другому с включением параметров «жадности» алгоритма и «стадности» алгоритма. Параметр «жадность» характеризует мотивацию, параметр «стадность» характеризует повторяемость поведения и является антонимом термина «случайность». Передача информации создает возможность самоорганизации системы колонии муравьев в достижении цели. Такая модель используется в мультиагентных системах.
Мультиагентная система [15] ищет оптимальное решение задачи без внешнего вмешательства. Под оптимальным решением понимается решение, на которое потрачено наименьшее количество энергии в условиях ограниченных ресурсов. Таким образом такое решение дает дополнительный эффект экономии ресурсов. Работа начинается с размещения муравьёв в вершинах графа (городах), затем начинается движение муравьёв – направление определяется вероятностным методом [13]. Напомним суть алгоритма. Муравьи первоначально перемещаются в случайном порядке по графу на рис. 2. После нахождения питания они возвращаются в свою колонию, при этом отмечают феромонами путь движения. Феромон – вещество, которое с течением времени испаряется. Если другие муравьи находят такие тропы, то они пойдут по ним. При нахождении питания и возвращении они укрепляют этот маршрут своими феромонами.
Со временем феромонная тропа начинает испаряться, тем самым уменьшая свою привлекательную силу. Чем больше времени требуется для прохождения пути до цели и обратно, тем сильнее испарится феромонная тропа. Чем больше питания на конце тропы, тем больше муравьев пройдут по пути и тем сильнее будет фермонная привлекательность. Это мотивирует к движению по тропам ведущим к максимальным ресурсам. Это и есть пример жадного алгоритма. Так алгоритм обеспечивает ресурсность решения задачи.
Другой аспект алгоритма пространственное решение. На коротком пути прохождение будет более быстрым и как следствие, плотность феромонов остаётся более высокой, чем по длинному маршруту. Это мотивирует муравьев к движению по коротким маршрутам к источникам питания. Данный подход может применяться при пространственном анализе и геоинформационном прогнозировании [16].
Испарение феромонов создает условие исключения локально-оптимального решения. Если бы феромоны не испарялись, то путь, выбранный первым, был бы самым привлекательным. В этом случае, исследования пространственных решений были бы ограниченными. Однако на практике существует иная ситуация. Если другой муравей находит более короткий путь от колонии до источника пищи, чем первый муравей, то он создает большую плотность формонов по этому пути. Другие муравьи, скорее всего, пойдут по этому пути, и алгоритм такого поведения в конечном итоге приводит всех муравьёв к оптимальному пути.
Недостатком метода является требование наличия колонии муравьев. Математически это требование заключается в множественности точек поиска. Поэтому начало поиска решения находится не в начальной точке Ab , в совокупности множества точек следующего ряда AN. Такой алгоритм оправдывает себя в сложных ситуациях типа поиска маршрута в системах GRID [17] или в комбинации с генетическими алгоритмами [18]. Но принципиально он требует множества точек поиска или дополнительных затрат на выбор путей.
При решении практических задач модель Ant Colony Algorithm (АСА) дополняется цепочкой обратной связи и банком данных [19]. Это приводит к дополнительному механизму: инкрементное накопление знаний и ресурсов; применение инкрементных знаний и ресурсов для решения очередного этапа задачи [20]. В результате работы этого механизма на каждом этапе получают инкрементные ресурсы (ИР) и инкрементные знания (ИЗ). Эти инкрементные величины помещают на хранение в банк данных и используют для решения задачи следующего этапа. На каждом этапе происходит решение задач с помощью АСА и накопление ресурсов и знаний. Итогом многократного решения задачи будут суммарные информационные ресурсы (СИР) и суммарные знания (СЗ).
СИР = ИР1 + ИР2 + ….. ИРn,
CЗ = ИЗ1 + ИЗ2 + …. ИЗn.
Здесь n- число этапов решения задачи
На основе накопленных знаний могут формироваться правила поиска маршрутов или правила прохождения определенных ситуаций.
Одной из основных характеристик такого решения является допустимое время решения, то есть интервал времени, в течение допускается решение задачи. В муравьином алгоритме такого ограничения нет. Информационное технологическое обеспечение инкрементного решения включает совокупность правил.
Выводы
В ходе данной работы использовалась дуальность понятий: математическое решение задачи и принятие решений (в управлении). Не потребовалось разграничение этих понятий, что дает основание говорить об универсальности метода. Дополнение муравьиного алгоритма механизмом инкрементного получения ресурсов и механизмом накопления ресурсов позволяет переносить решение данной задачи в область компьютерного и информационного моделирования. Накопление ресурсов в банке данных, как позволяет проводить системный анализ решений и проводить дополнительную оптимизацию на найденных решениях. Недостатком алгоритма является ограничение типа допустимого времени решения. Этот недостаток требует привлечения больших вычислительных ресурсов.
Результаты исследований показали применимость метода для поиска математических решений и для поиска управленческих решений. Это повышает ценность метода. Расширение муравьиного алгоритма механизмом инкрементного наращивания ресурсов, позволяет по мере накопления опыта переводить сложные задачи второго рода в категорию обозримых задач первого рода и упрощать управление сложными системами. Этот механизм позволяет проводить оптимизацию управления энергетическими и информационными ресурсами.

